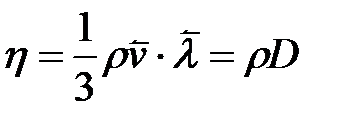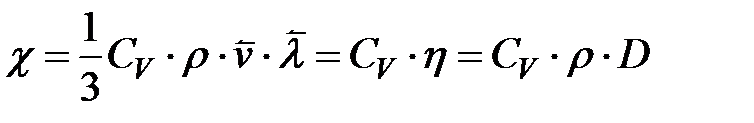Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Явище дифузії. Закон Фіка. Коефіцієнт самодифузії.Содержание книги Поиск на нашем сайте Явище дифузії 1. Знайомство з явищем. У повітрі розповсюджуються запахи, розчиняється цукор у воді, склеювання матеріалів, паяння і т.д. У тих випадках, коли в хімічно чистому однорідному газі концентрація молекул буде різною, спостерігається перенос молекул, що приводить до вирівнювання густин (або концентрацій) молекул. Це явище самодифузії. 2. Визначення. Явище проникнення молекул однієї речовини у проміжки між молекулами іншої речовини називається дифузією. 3. Умови протікання явища. Явище протікає при будь-яких умовах (бо молекули весь час перебувають у хаотичному русі), але з підвищенням температури інтенсивність протікання явища зростає. 4. Явище дифузії описується законом Фика 5. Пояснюється явище хаотичним рухом молекул.
Закон Фіка 1. Описує явище самодифузії. 2. Визначення. Маса газу, що переноситься через площину ΔS, перпендикулярну до напрямку переносу за час Δt, прямо пропорційна коефіцієнту самодифузії D.
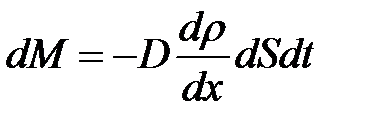 , де D - коефіцієнт самодифузії, , де D - коефіцієнт самодифузії, 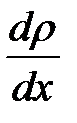 - градієнту густини, ΔS - розміри площини Δt - час спостереження Δt. Знак мінус показує, що маса газу переноситься в напрямку убування густини. - градієнту густини, ΔS - розміри площини Δt - час спостереження Δt. Знак мінус показує, що маса газу переноситься в напрямку убування густини.
4. Описує явище самодифузії в газах. Коефіцієнт самодифузії D 1. Характеризує явище самодифузії в газах. 2. Визначення. Коефіцієнт самодифузії чисельно дорівнює масі газу, що переноситься за одиницю часу через одиничний площину перпендикулярний напрямку переносу, при градієнті густини рівному одиниці. 3. Коефіцієнт самодифузії – це скалярна величина. 4. 5.
Внутрішнє тертя (в'язкість). Закон Ньютона для внутрішнього тертя. Коефіцієнт внутрішнього тертя. Зв'язок між коефіцієнтами для явища переносу Внутрішнє тертя (в'язкість) 1. Явище внутрішнього тертя спостерігається в тому випадку, коли різні шари газу рухаються з різними швидкостями. У цьому випадку більш швидкі шари гальмуються тими, що рухаються повільніше. На макроскопічний рух шарів газу (тобто рух шару як цілого) виявляє вплив мікроскопічний тепловий рух молекул. 2. Визначення. Внутрішнє тертя або в’язкість - це властивість рідин і газів чинити опір переміщенню однієї їх частини відносно іншої. 3. Явище описується законом Ньютона. 4. Пояснення явища. Розглянемо шар газу 1, що рухається зі швидкістю v1 і шар газу 2, що рухається зі швидкістю v2 v1 > v2 (рис. 3). У результаті теплового хаотичного руху молекула A із шару 1 перейде в шар 2 і змінить свій імпульс від значення mv до якогось значення mv’ (v2 < v’ < v1). Молекула В із шару 2 у результаті теплового хаотичного руху перейде в шар 1 і змінить свій імпульс від значення mv2 до значення mv’ ’ (v2 < v’’ < v1), тобто молекули раніше колишні в шарі 2, виявившись у шарі 1, при зіткненні з його молекулами прискорюють свій упорядкований рух, а молекули, що рухаються у шарі 1 уповільнюються. Навпаки, при переході молекул із шару, що більш швидко рухається, 1 у шар 2 вони переносять більші імпульси
Закон Ньютона для внутрішнього тертя 1. Описує явище внутрішнього тертя. 2. Визначення. Сила внутрішнього тертя F, що діє між двома шарами газу прямо пропорційна коефіцієнту внутрішнього тертя η, градієнту швидкості й величині площі ΔS.
 , де η - коефіцієнт внутрішнього тертя, , де η - коефіцієнт внутрішнього тертя,  - градієнт швидкості, dS елемент площини dt - час спостереження. - градієнт швидкості, dS елемент площини dt - час спостереження.
Знак мінус показує, що сила внутрішнього тертя протилежна градієнту швидкості, тобто імпульс переноситися в напрямку убування швидкості.
Коефіцієнт внутрішнього тертя η 1. Коефіцієнт внутрішнього тертя характеризує здатність рідин і газів чинити опір переміщенню однієї їх частини відносно іншої. 2. Коефіцієнт внутрішнього тертя (в’язкості) η чисельно дорівнює силі внутрішнього тертя, що діє на одиницю площі, якщо градієнт швидкості шарів дорівнює одиниці. 3. Коефіцієнт внутрішнього тертя – це скалярна величина. 4. 5.
Зв'язок між коефіцієнтами для явища переносу
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 787; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

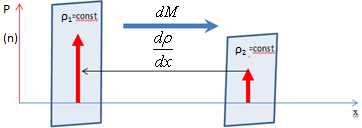
 Згідно з кінетичною теорією газів
Згідно з кінетичною теорією газів 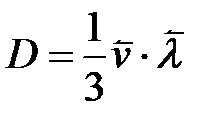 .
.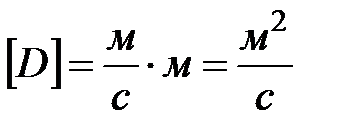
 і міжмолекулярні зіткнення в шарі 2 прискорюють рух молекул цього шару.
і міжмолекулярні зіткнення в шарі 2 прискорюють рух молекул цього шару.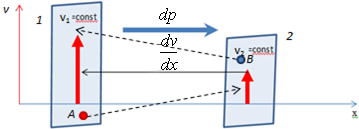
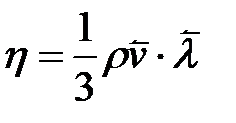
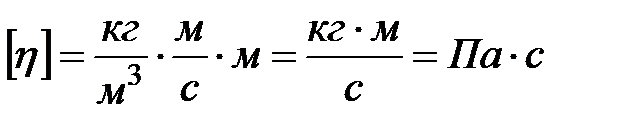 .
.