
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод монте-карло и проверка статистических гипотезСодержание книги
Поиск на нашем сайте
Статистические испытания по методу Монте-Карло представляют собой простейшее имитационное моделирование при полном отсутствии каких-либо правил поведения. Получение выборок по методу Монте-Карло - основной принцип компьютерного моделирования систем, содержащих стохастические или вероятностные элементы. Зарождение метода связано с работой фон Неймана и Улана в конце 1940-х гг., когда они ввели для него название «Монте-
БИБЛИОТЕКА Поволжской академии Государственной службы
НЕТРАДИЦИОННЫЕ СЕТЕВЫЕ МОДЕЛИ И ВРЕМЕННЫЕ ДИАГРАММЫ ИНТЕРВАЛОВ АКТИВНОСТИ Основа концепции имитационного инструментария, с помощью которого можно проводить структурный анализ и имитационное моделирование, заключается в механизмах, позволяющих агрегировать элементарные процессы и устанавливать между ними функциональные связи (причинно-следственные, информационные, финансовые и иные). Ниже предлагается сетевая концепция, существенно отличающаяся от аналитического аппарата, рассмотренного в литературе по теории массового обслуживания, использующая удачные результаты теории стохастических сетей и численные методы, основанные на диффузной аппроксимации процессов массового обслуживания. Эта концепция разработана, в первую очередь, для последующей реализации имитационных механизмов в рамках специального пакета имитационного моделирования. Она предназначена для верификации работоспособности пакета, для оценочных расчетов при отладке имитационных моделей, но не предназначена для практических расчетов показателей риска по аналитическим формулам. Идею предлагаемой концепции рассмотрим на примере из конкретного проекта «Открытое образование» («е-образование»), реализуемого под патронажем Международной академии открытого образования (МАОО). Учебные процессы в открытом образовании. Учебный процесс - это понятие, охватывающее всю учебную деятельность классического университета. Учебный процесс состоит из многих компонентов: процесса обучения студента по конкретной специальности в течение пяти лет, семестрового учебного процесса на потоке, процесса изучения дисциплины. Классический университет имеет жесткий избыточный набор ресурсов, который позволяет реализовать учебный процесс в любой его интерпретации. Однако такой фиксированный набор приводит к издержкам планирования, к удорожанию обучения студента без гарантий высокого качества. В открытом образовании работают специалисты, имеющие квалификацию не ниже, чем в классическом университете. Единственное, что их отличает, - это различные образовательные технологии (классическая и комплексная). ■Процессом* изучения дисциплины (далее - процессом) в распре-яином институте назовем неделимую функцию освоения дисцип-етудентом по утвержденной программе. Для реализации про-необходимы различные ресурсы. IB системе открытого образования ресурсы используются в раешном режиме. Ресурсы распределенного института можно на два типа: интеллектуальный ресурс (учитель) и учебный (далее - просто ресурс). Учителя - это преподаватели кафедр, тренеры учебно-овйчньгх фирм, тьюторы-консультанты. Учителя предметно ятея к разным распределенным кафедрам через механизм «ат-;ии». Ресурсы - это комплекты учебно-практических пособий, студии и есть дистанционная фаза типа телеконференции), режимы рнет-доступа, аудитории (если есть очная фаза) и другие, без •рых обучение студента может не состояться. Процесс запущен, если возникла необходимость изучения дис-ы и распределенный институт имеет для этого ресурсы. За-процесса не означает, что в любой момент времени будет хотя один студент, изучающий эту дисциплину. Соответственно про- может быть снят (или отменен). Далее будем полагать, что распределенный институт ориентиро-йрежде всего на индивидуализацию обучения студента. Поэтому том случайных явлений, не зависящих от распределенного ин-а, при массовом обслуживании студентов возможны техноло-кие задержки: очереди к учителям и задержки из-за временной катки ресурсов. Возникает задача определения такого числа ре-в, при котором процесс обучения по конкретной специально-ршел бы продолжительность не хуже заданной с учетом техно-;ческих задержек. ||При реализации обучения по специальности процессы могут причинно-следственные связи. Поэтому можно говорить о что они образуют направленный граф (рис. 1.7). Применение >дов сетевого планирования и управления невозможно; основная ость - это циклы. Циклы возникают по двум причинам: сту-обучаются не по жесткому учебному плану (возможны раз-ые индивидуальные планы), для отстающих студентов органи-
Рассмотрим возможные диаграммы состояний процесса (рис. 1.8). Если мощности ресурсов бесконечны либо каждый процесс используется вместе с постоянно закрепленными за ним ресурсами, то возможны два состояния (рис.1.8,а): ожидание студентов (ЖС) и выполнение процесса изучения дисциплины (ПУ). В таких ситуациях не возникает необходимости в незапланированных ресурсах: у студента есть учебный план. В состояние ПУ процесс попадает, получив студента от процесса-производителя. После изучения дисциплины студент переходит к процессу-потребителю и попадает в состояние ЖС, если какой-либо производитель не подготовил следующего студента. В более реальном случае (рис. 1.8,6) при конечных мощностях глобальных ресурсов появляется состояние ожидания ресурса, когда процессу (точнее, студенту в процессе изучения дисциплины) нужны ресурсы (HP). В условиях реального университета, когда обучение контролируется, а выделение ресурсов и их возвращение осуществляется с помощью процессов планирования и распределения ресурсов, вво- еще два состояния (рис.1.8,в): подготовка к выполнению (ТВ) ^завершение выполнения - контрольные мероприятия, экзамены, (ЭЗ).
k- Когда возникает потребность в незапланированных ресурсах, то «ожны обратные переходы типаПУ-»НР (рис. 1.8,5,1.8,в). Такие гходы могут привести к блокировкам, которые можно разрешить ющью известных решений задачи взаимного исключения.
Во время подготовки к выполнению (ГВ) осуществляется плани-ie ресурсов, а после завершения (ЭЗ) - возврат ресурсов в рас-яше планирующих и распределяющих процессов. Организация и взаимосвязь различных компонентов системы от-•го образования может быть рассмотрена относительно управ-процессами в следующих подразделениях университета tc. 1.9):
• управления учебной и учебно-методической работой (УУМР), • дирекции распределенного университета, которая совместно с
[егоГОС); • кафедр (распределенных кафедр открытого образования). Ка- ^подавательского состава, тренеров (тьюторов-консультантов), жирантов, докторантов и других преподавателей). Далее перейдем к оценке времени изучения студентами дисцип-_j учебного плана. Время прохождения всех дисциплин учебного гана студентом - это время пребывания заявки в стохастической ги (см. рис. 1.7). Заявки в такой сети будем называть «транзакта-[», чтобы отличать от других элементарных заявок. Транзакт, попадая из одного узла сети (процесс-производитель) в -ой узел (процесс-потребитель), свидетельствует о необходимо-изучения студентом следующей дисциплины учебного плана. Joane этого процесс-потребитель выводится из состояния ЖС и юпадает в состояние ГВ. После выделения ресурсов (HP), выполнения функции (ПУ) и завершения выполнения контрольных мероприятий (ЭЗ) транзакт появляется на выходе узла-производителя, а •цесс возвращается в состояние ЖС. Случайный интервал време-ограниченный моментом выхода процесса из состояния ЖС в яале изучения дисциплины и ближайшим моментом попадания в [ало состояние, назовем интервалом активности процесса. Длительность пребывания транзакта в соответствующем узле - это интервал [i активности. Для оценки времени реакции системы открытого обра-^„Зования, реализуемой в рамках распределенного института по учеб-f;HOMy плану, необходимо уметь рассчитывать значения интервалов (-(^тивности всех процессов, входящих в состав сети. % Оценка интервала активности процесса. Далее построим ите-ирационную процедуру, позволяющую провести соответствующие ^оценки. Обозначим А - начало очередной итерации; Б - конец оче-|редной итерации.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.100.101 (0.011 с.) |







 1.4
1.4 В университетах используется более подходящее слово «курс». Однако в есах поддержки общности с экономикой используется термин «процесс».
В университетах используется более подходящее слово «курс». Однако в есах поддержки общности с экономикой используется термин «процесс». зуется повторное обучение (возврат к пройденной ранее, но не защищенной дисциплине для ее более глубокого изучения). Относительно пути студента по графу в каждый момент времени он находится в определенном текущем процессе, - в узле графа. Процесс, который передал студента в текущий процесс, назовем прои&одите-лемь а процесс, который примет студента после завершения текущего, назовем потребителем.
зуется повторное обучение (возврат к пройденной ранее, но не защищенной дисциплине для ее более глубокого изучения). Относительно пути студента по графу в каждый момент времени он находится в определенном текущем процессе, - в узле графа. Процесс, который передал студента в текущий процесс, назовем прои&одите-лемь а процесс, который примет студента после завершения текущего, назовем потребителем.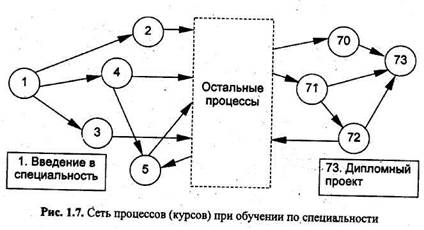


 1\ • учебно-методологического совета (УМС), который работает дирекции в качестве коллегиального совещательного органа для >янного совершенствования государственных образовательных __лартов (ГОС), изменяющихся примерно раз в пять лет, и учеб-IJoro плана, который корректируется ежегодно (в рамках действую-
1\ • учебно-методологического совета (УМС), который работает дирекции в качестве коллегиального совещательного органа для >янного совершенствования государственных образовательных __лартов (ГОС), изменяющихся примерно раз в пять лет, и учеб-IJoro плана, который корректируется ежегодно (в рамках действую-













