Утворення та задання поверхонь.

Лекція 4

ПОВЕРХНІ

 

Утворення та задання поверхонь.

Поверхня в геометрії визначається як двопараметрична множина точок простору, тобто множина точок простору, координати яких є диференційованими функціями двох параметрів. Це визначення дозволяє розглянути поверхню як неперервну множину послідовних положень змінної лінії – твірної, що рухається в просторі за певним правилом, або перетин твірної (у всіх її послідовних положеннях), з деякими фіксованими лініями, які називаємо напрямними.

 

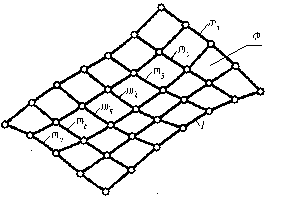
Рис. 4.1

В нарисній геометрії користуються головним чином кінематичним способом утворення поверхонь. На поверхні Ф можливо в загальному випадку провести два типи сімейства ліній l та m, яким будуть задовольняти слідуючі умови:

-ніякі дві лінії одного сімейства не перетинаються між собою.

-кожна лінія одного сімейства перетинає всі лінії другого.

На рис. 4.1 поверхня Ф утворена рухом твірної l по нерухомим напрямним m. Твірні та напрямні можуть мінятись місцями.

З великої кількості поверхонь оточуючого нас простору ми будемо розглядати два класи, поверхні обертання і гранні поверхні.

Поверхнею обертання називається поверхня, яка описується якою-небудь лінією (прямою, кривою) твірною при її обертанні навколо нерухомої осі.

Визначник поверхні обертання: 1. Нерухома пряма – вісь обертання; твірна - пряма або крива лінія. 2. Твірна обертається навколо осі так, щоб кожна точка твірної здійснила повний оберт.

Щоб викреслити складну деталь, треба навчитись будувати прості геометричні фігури, форми яких складають деталі: призми, циліндри, сфери, конуси, піраміди. Проектування геометричних тіл заключається не тільки в побудові за заданими розмірами проекцій цих тіл, але і в умінні провести повний аналіз креслення, тобто вказати ребро, вершини, грані, визначити взаємне розміщення цих елементів, знайти видимі і невидимі частини фігури, визначити проекції точок, які лежать на поверхні тіла, тощо.

Положення точки, яка лежить на поверхні задана, якщо відома одна її проекція і вказано, на якій частині поверхні (видимої або невидимої) точка розміщена. Якщо немає вказівок, вважають, що точка розміщена на видимій частині поверхні.

Щоб побудувати недостаючі проекції точки яка лежить на поверхні, необхідно: 1) визначити вид поверхні (проектуюча або загального положення) на якій лежить задана точка; 2) вибрати графічно просту для побудови на кресленні лінію поверхні яка б проходила через задану точку; 3) побудувати проекції цієї лінії на кресленні; 4) побудувати шукані на кресленні задані точки.

Будь-яка лінія являє собою сукупність точок, тому побудова проекцій лінії, розміщеної на поверхні, зводиться до побудови проекцій декількох точок, які належать цій лінії.

Розглянемо деякі поверхні, утворені обертанням прямої лінії.

 

Відображення поверхонь.Точки на поверхнях

Циліндр.

 

Циліндром називається тіло, обмежене циліндричною поверхнею і двома паралельними площинами (основами). Прямим називається циліндр, в якого твірні перпендикулярні до основи рис. 4.2,а.

Проводячи аналіз креслення циліндра можна відмітити, що верхня основа циліндра паралельна площині ¹ П, нижня основа належить ¹ П. Бокова циліндрична поверхня – горизонтально – проектуюча. На ¹ П вона проектується в коло. Твірні даної поверхні (позначені як а, b, c, d) являються горизонтально-проектуючими прямими.

Розглянемо аксонометричне зображення циліндра (рис. 4.2,б) на горизонтальній проекції видимою буде верхня основа циліндра. На фронтальній проекції видимою буде передня частина циліндра (до площини d). Площина d умовно поділяє зображення циліндра на фронтальній площині проекцій на видиму і невидиму частини. Площина e розділяє поверхню циліндра на видиму і невидиму частини на профільній площині проекцій. ³ П. Всі точки, що знаходяться зліва від даної площини на профільній площині ³ П будують видимі, а точки, що знаходяться справа – невидимі. Невидимі точки на комплексному кресленні зображуються в круглих дужках (точка E на рис. 4.2,е).

Побудова всіх проекцій точок здійснюється з допомогою ліній зв’язку по відповідних координатах. Яку б точку ми не взяли на поверхні циліндра, горизонтальна проекція цієї точки буде знаходитись на основі циліндра, тобто на колі.

Розглянемо декілька прикладів знаходження проекцій точок.

1. Задано: точка А на фронтальній проекції належить твірній а та верхній основі a. У символьному записі - ² А Ì ² а ̲a (рис. 4.2,в).

Рис. 4.2

Креслення: проекція точки ¹ А на горизонтальній площині співпадає із проекцією твірної ¹ А º ¹ а. Проекція точки ³ А на профільній площині проекцій співпадає із профільною проекцією твірної ³ а та належить верхній основі - ³a (твірна - а належить фронтальній площині g, що проходить через вісь симетрії (див. рис. 4.2, б) тому на профільній площині не викреслюється).

2. Задано: точка В на фронтальній проекції належить верхній основі a та боковій поверхні g. У символьному записі - ² B Ì a² ̲g (рис. 4.2,г).

Креслення: проекція ¹ В на горизонтальній площині видима і знаходиться на колі основи. Проекція ³ В на профільній площині проекцій видима належить верхній основі - ³a і знаходиться вправо від осі симетрії на відстані y_B

3. Задано: на фронтальній проекції точка C належить боковій поверхні g. У символьному записі - ² C ̲g (рис. 4.2,д).

Креслення: проекція ¹ С на горизонтальній площині видима і знаходиться на колі основи. Проекція ³ С на профільній площині проекцій видима і знаходиться від проекції ² С по горизонтальній лінії з’вязку вправо від осі симетрії на відстані y_С

4. Задано: на фронтальній проекції точка D належить боковій поверхні g. У символьному записі – ² D ̲g (рис. 4.2,д).

Креслення: проекція ¹ D на горизонтальній площині видима і знаходиться на колі основи. Проекція ³ D на профільній площині проекцій невидима і знаходиться від проекції ² D по горизонтальній лінії з’вязку вправо від осі симетрії на відстані y_D

5. Задано: невидима на фронтальній проекції точка E належить боковій поверхні g. У символьному записі – ² E ̲g (рис. 4.2,е).

Креслення: проекція ¹ E на горизонтальній площині видима і знаходиться на колі основи. Проекція ³ E на профільній площині проекцій невидима і знаходиться від проекції ² E по горизонтальній лінії з’вязку вліво від осі симетрії на відстані y_E

Сфера.

Сферична поверхня може бути одержана шляхом обертання кола навколо осі, яка лежить в площині кола і проходить через його центр. Рис. 4.3,а.

Проекції контуру сфери на епюрі представляють собою кола які зображені на рис. 4.3,б. Довільний перетин сфери площиною рівня (горизонтальна, фронтальна, профільна) утворює коло і воно проектується без спотворення на відповідну площину проекцій.

Горизонтальна площина проходить через центр сфери і ділить її на дві рівні частини. Коло, що утворюється в перетині, називається екватор. Верхня половина сфери дає видимі точки на горизонтальній проекції (точки D і E на рис. 4.3,г), а нижня – невидимі.

Фронтальна площина також ділить сферу на дві рівні частини. Коло, що утворюється в перетині, називається головний мередіан. Точки, які знаходяться попереду цієї площини на фронтальній проекції видимі (точка F на рис. 4.3,д), які позаду – невидимі(точка G на рис. 4.3,д).

Ще одне коло одержимо як січення профільною площиною. Коло, що утворюється в перетині, називається профільний мередіан. Точки будут видимі на профільній проекції, тоді коли вони будуть з лівої сторони від цієї січної площини (точки F і G на рис. 4.3,д), і невидимі, коли вони будуть справа (точки H і I на рис. 4.3,е).

Розглянемо декілька прикладів знаходження проекцій точок.

1. Задано: точка А на фронтальній проекції знаходиться в перетині головного фронтального та профільного мередіанів. У символьному записі - ² А Ì ² b Dz c (рис. 4.3,в). (Аналогічно можно провести аналіз побудови точки В, що знаходиться в перетині екватора та профільного мередіана та аналіз побудови точки C що знаходиться в перетині екватора та головного мередіана)

Креслення: проекція точки ¹ А на горизонтальній площині буде знаходитись в перетині головного фронтального та профільного мередіанів- ¹ А Ì ¹ b ǹ c. Проекція точки ³ А на профільній площині буде знаходитись в перетині головного фронтального та профільного мередіанів- ³ А Ì ³ b dz c.

Аналогічно можно провести аналіз побудови точки B, що знаходиться в перетині екватора та профільного мередіана та аналіз побудови точки C що знаходиться в перетині екватора та головного мередіана (рис. 4.3,в)

2. Задано: точка D на фронтальній проекції належить головному (фронтальному) мередіану. У символьному записі – ² D Ì ² b (рис. 4.2,г).

Креслення: проекція точки ¹ D на горизонтальній площині буде знаходитись на перетині вертикальної лінії з’вязку і осьової лінії, а саме належати головному мередіану – ¹ D Ì ¹ b. Координата точки D по осі ОХ визначається колом радіусом – R1 утвореним в горизонтальній площині.

Аналогічно можно провести аналіз побудови точки E, (рис. 4.3,г) її проекція на горизонтальній площині визначається екватором сфери– ¹ E Ì ¹ a, фронтальна проекція буде знаходитись на перетині вертикальної лінії з’вязку і осьової лінії – ² E Ì ² b. Координата точки E на профільній проекції визначається колом радіусом – R3 утвореним в профільній площині.

3. Задано: точка F - видима та точка G - невидима на фронтальній проекції. У символьному записі – ² F º ² G (рис. 4.3,д).

Креслення: проекції точок ¹ F і¹ G на горизонтальній площині будуть знаходитись на колі радіусом – R1, його радіус визначено з фронтальної площини проекцій. Проекції точок ³ F і³ G на профільній площині будуть знаходитись на колі радіусом – R3, його радіус визначено з фронтальної площини проекцій.

4. Задано: точка H - видима та точка I - невидима на горизонтальній проекції. У символьному записі – ² H º ² I (рис. 4.3,е).

Креслення: проекції точок ² H і² I на горизонтальній площині будуть знаходитись на колі радіусом – R2, його радіус визначено з фронтальної площини проекцій. Проекції точок ³ F і³ G на профільній площині будуть знаходитись на колі радіусом – R3, його радіус визначено з фронтальної площини проекцій.

Рис. 4.3

Конус.

Конус – геометричне тіло, обмежене боковою конічною поверхнею - b і площиною основи - a, що перетинає всі його твірні. Основа конуса лежить в площині ¹ П. Прямим круговим називається конус, у якого основа є коло, а висота проходить через центр основи. Бічна поверхня прямого конуса утворена твірними які проходять через загальну точку S - вершину конуса (див.рис 4.4,а). На рис. 4.4,б зображено проекції конуса на площини проекцій.

Твірні a, b є окреслюючими по відношенню до ² П, вони лежать у фронтальній площині. Твірні c, d – окреслюючі по відношенню до площини проекцій ³ П, знаходяться в профільній площині (рис. 4.4,в). Всі інші твірні конуса - прямі загального положення і на епюрі не зображуються.

Проекції точок, які лежать на основі конуса, знаходять на інших площинах проекцій за допомогою ліній зв’язку.

Розглянемо декілька прикладів знаходження проекцій точок.

1. Задано: проекція точки - ² С належить основі конуса (рис. 4.4,г).

Креслення: проекції точки - ¹ С на горизонтальній площині знайдемо на колі основи, а проекцію точки - ³ С на профільній площині знайдемо на відстані Y_С в напрямку додатніх значень осі координат – Y.

2.Задано: точки – ¹ D і ¹ E, що належать окреслюючим твірним -¹ d, ¹ c конуса (рис. 4.4,д).

Необхідно: Побудувати проекції точок. Вказати іх видимість.

Аналіз: На горизонтальній проекції видимою буде вся бічна поверхня конуса. Фронтальні окреслюючі твірні ² а, ² в ділять бічну поверхню конуса на передню - видиму і задню - невидиму (по відношенню до ² П – рис. 4.4.д). Профільні окреслюючі твірні -³ d, ³ c ліву видиму і праву невидимі частини (по відношенню до ³ П, рис. 4.4. д).

Креслення: Проведемо горизонтальну площину - ²g через фронтальну проекцію точки – (² D) –невидима, та горизонтальну площину - ²dчерез фронтальну проекцію точки – ² E. Побудуємо коло радіусом - R1 в площині ¹g та коло радіусом – R2 в площині - ²d на горизонтальній площині проекцій. Проекції точок – ¹ D і ¹ E на горизонтальній площині знайдемо в перетині кіл радіусами R1 та R2 з горизонтальною проекцією окреслюючих твірних - ¹ d, ¹ c. Профільні проекції точок- ³ D і ³ E знаходяться в перетині горизонтальних ліній зв’язку від фронтальних проекцій точок- ² D і ² E та профільних проекцій окреслюючих твірних - ³ d та³ c.

3. Задано: точка – ² F, що належить конічній поверхні (рис. 4.4,е).

Креслення: Проведемо горизонтальну площину - ²e через фронтальну проекцію точки – ² F. Побудуємо коло радіусом - R1 в цій площині на горизонтальній проекції. Горизонтальну проекцію точки - ¹ F знайдемо в перетині цього кола і вертикальної лінії зв’язку від фронтальної проекції точки – ² F. Профільну проекцію точки – ³ F знайдемо в площині - ³e на відстані Y_F в напрямку додатніх значень осі координат – Y.

 

Рис. 4.4

Призма.

 

Призма – многогранник, утворений перетином призматичної поверхні двома паралельними площинами -a і b. На рис.4.5,а зображені проекції призми і її деяких складових елементів. Елементами призм вважають: вершини (точки), ребра (прямі), грані (площини). Призму називають прямою, якщо бокові ребра її перпендикулярні до основи. Призму називають правильною, якщо в основі її лежить правильний многокутник. Аксонометричне зображення призми наведено на рис. 4.5,б.

Призма, яку зображено на рис.4.5,в має 6 граней, 2 основи, 18 ребер (із них 6 бокових –a, b, c, d, e, f), 12 вершин. Верхня основа паралельна горизонтальній площині проекцій ¹ П нижня – належить ¹ П. Грані ВСМК, FEOT – фронтальні площини. На ³ П кожна з них проектується в лінію – слід площини. Інші грані – горизонтально-проектуючі площини. Ребра основи – горизонтальні лінії рівня. На горизонтальній проекції видимою буде верхня основа призми. На фронтальній проекції видимі грані АВKL, ВСМК, СDNM, інші – невидимі. На профільній проекції видимі грані – ABKL, АFТL, інші – невидимі.

Комплексне креслення правильної призми слід починати з горизонтальної проекції. Побудову всіх проекцій точок на боковій поверхні призми здійснють за допомогою ліній зв’язку по відповідних координатах. Яку б точку ми не взяли на боковій поверхні призми, горизонтальна проекція цієї точки буде знаходитись в основі призми.

Розглянемо декілька прикладів знаходження проекцій точок.

1. Задано: проекція точки - ² P належить грані ABKL (площина - g, див.рис. 4.5,г).

Креслення: горизонтальна проекція точки – ¹ P знаходиться в основі призми на ребрі – ¹ K ¹ L. Профільну проекцію точки – ³ P знаходимо на горизонтальній лінії з’вязку, яку проводимо від фронтальної проекції точки – ² P,на відстані Y_P в напрямку додатніх значень осі координат – Y.

2. Задано: проекція точки – ² S належить грані CDNM (площина - d, див.рис. 4.5,д).

Аналіз: грань CDNM видима на горизонтальній, фронтальній та невидима на профільній проекціях (див. рис.4.5,б), аналогічно позначимо проекції точки – ¹ S, ² S і (³ S).

Креслення: горизонтальна проекція точки – ¹ S знаходиться в основі призми на ребрі – ¹ N ¹ M. Профільну проекцію точки – ³ P знаходимо на горизонтальній лінії з’вязку, яку проводимо від фронтальної проекції точки – ² P,на відстані Y_S в напрямку додатніх значень осі координат – Y.

3. Задано: проекція точки – ² I належить грані BCMK (площина - ²e, див.рис. 4.5,e).

Аналіз: грань BCMK – фронтальна площина.

Креслення: горизонтальна проекція точки – ¹ I знаходиться в основі призми на ребрі – ¹ K ¹ M. Профільну проекцію точки – ³ I знаходимо по горизонтальній лінії з’вязку на проекції грані BCMK (площина - ³e).

Рис. 4.5

Піраміда.

Піраміда – многогранник, утворений перетином пірамідальної поверхні площиною основи -a. На рис.4.6,а зображені проекції піраміди і її деяких складових елементів. Елементами пірамід вважають: вершини (точки), ребра (прямі), грані (площини). Піраміду називають прямою, якщо її висота перпендикулярна основі. Піраміду називають правильною, якщо в основі її лежить правильний многокутник. Аксонометричне зображення піраміди наведено на рис. 4.6,б.

Піраміда, яку зображено на рис.4.6,в має 6 граней, 1 основу, 12 ребер (із них 6 бокових), 7 вершин. Основа піраміди належить горизонтальній площині проекцій ¹ П або паралельна їй. Бокові ребра SA та SD - фронтальні прямі рівня. Інші бокові ребра – прямі загального розташування. Ребра основи – горизонтальні лінії рівня. На горизонтальній проекції видимими будуть всі грані піраміди. На фронтальній проекції видимі грані SAB, SBC, SCD, інші – невидимі. На профільній проекції видимі грані – SAB, SAF, інші – невидимі.

Комплексне креслення правильної піраміди слід починати з горизонтальної проекції.

Розглянемо декілька прикладів знаходження проекцій точок.

1. Задано: проекція точки – ² G належить ребру - AB в основі піраміди(площина - a, див.рис. 4.6,г).

Креслення: горизонтальна проекція точки – ¹ G знаходиться в основі піраміди на ребрі – ¹ A ¹ B. Профільну проекцію точки – ³ G знаходимо на горизонтальній лінії з’вязку,яку проводимо від фронтальної проекції точки – ² G,на відстані Y_G в напрямку додатніх значень осі координат – Y.

2. Задано: проекція точки – ² H належить боковому ребру SB (див.рис. 4.6,д).

Креслення: горизонтальна проекція точки – ¹ H знаходиться в перетині вертикальної лінії з’вязку та ребра – ¹ S ¹ B піраміди. Профільну проекцію точки – ³ H знаходимо на перетині горизонтальної лінії з’вязку, яку проводимо від фронтальної проекції точки – ² H,із ребром -³ S ³ B.

3. Задано: проекція точки – ² I належить грані SAB (див.рис. 4.6,e).

Аналіз: грань SAB – площина загального розташування.

Креслення: Проведемо горизонтальну площину - ²b через фронтальну проекцію точки – ² I. Утворюється лінія перетину n, що належить горизонтальній площині - nÌ b. Горизонтальна проекція точки – ¹ I знаходиться на перетині вертикальної лінії з’вязку, яку проведено від фронтальної проекції точки – ² I, із горизонтальною проекцією лінії -¹ n. Профільну проекцію точки – ³ I знаходимо по горизонтальній лінії з’вязку, яку проводимо від фронтальної проекції точки – ² I,на відстані Y_I в напрямку додатніх значень осі координат – Y.

Рис. 4.6

Лекція 4

ПОВЕРХНІ

 

Утворення та задання поверхонь.

Поверхня в геометрії визначається як двопараметрична множина точок простору, тобто множина точок простору, координати яких є диференційованими функціями двох параметрів. Це визначення дозволяє розглянути поверхню як неперервну множину послідовних положень змінної лінії – твірної, що рухається в просторі за певним правилом, або перетин твірної (у всіх її послідовних положеннях), з деякими фіксованими лініями, які називаємо напрямними.

 

Рис. 4.1

В нарисній геометрії користуються головним чином кінематичним способом утворення поверхонь. На поверхні Ф можливо в загальному випадку провести два типи сімейства ліній l та m, яким будуть задовольняти слідуючі умови:

-ніякі дві лінії одного сімейства не перетинаються між собою.

-кожна лінія одного сімейства перетинає всі лінії другого.

На рис. 4.1 поверхня Ф утворена рухом твірної l по нерухомим напрямним m. Твірні та напрямні можуть мінятись місцями.

З великої кількості поверхонь оточуючого нас простору ми будемо розглядати два класи, поверхні обертання і гранні поверхні.

Поверхнею обертання називається поверхня, яка описується якою-небудь лінією (прямою, кривою) твірною при її обертанні навколо нерухомої осі.

Визначник поверхні обертання: 1. Нерухома пряма – вісь обертання; твірна - пряма або крива лінія. 2. Твірна обертається навколо осі так, щоб кожна точка твірної здійснила повний оберт.

Щоб викреслити складну деталь, треба навчитись будувати прості геометричні фігури, форми яких складають деталі: призми, циліндри, сфери, конуси, піраміди. Проектування геометричних тіл заключається не тільки в побудові за заданими розмірами проекцій цих тіл, але і в умінні провести повний аналіз креслення, тобто вказати ребро, вершини, грані, визначити взаємне розміщення цих елементів, знайти видимі і невидимі частини фігури, визначити проекції точок, які лежать на поверхні тіла, тощо.

Положення точки, яка лежить на поверхні задана, якщо відома одна її проекція і вказано, на якій частині поверхні (видимої або невидимої) точка розміщена. Якщо немає вказівок, вважають, що точка розміщена на видимій частині поверхні.

Щоб побудувати недостаючі проекції точки яка лежить на поверхні, необхідно: 1) визначити вид поверхні (проектуюча або загального положення) на якій лежить задана точка; 2) вибрати графічно просту для побудови на кресленні лінію поверхні яка б проходила через задану точку; 3) побудувати проекції цієї лінії на кресленні; 4) побудувати шукані на кресленні задані точки.

Будь-яка лінія являє собою сукупність точок, тому побудова проекцій лінії, розміщеної на поверхні, зводиться до побудови проекцій декількох точок, які належать цій лінії.

Розглянемо деякі поверхні, утворені обертанням прямої лінії.