
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изменчивость: изучение разнообразияСодержание книги
Поиск на нашем сайте
Изменчивость: изучение разнообразия
Одна из причин, по которым возникает необходимость в проведении статистического анализа, состоит в том, что данные изменчивы. Если бы данные не изменялись, то ответы на многие вопросы были бы просто очевидными и нам не нужно было бы обращаться к методам статистического анализа. Ситуация, в которой присутствует изменчивость, часто содержит риск, поскольку даже использование всей доступной информации не позволяет точно предугадать, что же произойдет в будущем. Для адекватной работы с риском необходимо понимать его природу и уметь измерять изменчивость (часто также используют термин “вариация”), которая является его следствием. Приведем несколько ситуаций, в которых изменчивость имеет важное значение. Случай первый. Рассмотрим изменчивость производительности труда работников. Совершенно очевидно, что эффективность работы отдела определяется общей производительностью труда всех его сотрудников. Однако любые усилия, направленные на повышение производительности труда, должны учитывать индивидуальные особенности работников. Например, некоторые программы повышения производительности труда могут быть ориентированы на всех работников, в то время как другие — уделять особое внимание самым “быстрым” или самым “медленным” из них. Определение изменчивости производительности труда дает возможность выявить разброс таких индивидуальных различий и получить полезную информацию для планирования мероприятий по повышению общей производительности труда. Случай второй. Фондовая биржа в среднем обеспечивает более высокую доходность вложенных средств, чем, например, фонды денежного рынка. Однако работа на фондовой бирже связана с большим риском, и инвестирование в акции может привести к реальным потерям. Таким образом, средняя, или “ожидаемая” доходность не отражает полностью всю картину. Мера изменчивости доходности отдельных инвестиций будет отражать уровень риска, сопряженного с каждым конкретным вложением средств. Случай третий. Предполагается, что вы сравниваете маркетинговые затраты своей фирмы с аналогичными затратами фирм, работающих в вашей отрасли промышленности, и обнаруживаете, что затраты вашей фирмы меньше затрат, типичных для данной отрасли. Для того чтобы оценить затраты на будущее, очень полезным может оказаться учет разброса соответствующих данных по отрасли. Найдя разность между значением затрат своей фирмы и средним значением по отрасли и сравнив полученную величину с мерой изменчивости затрат в отрасти, можно сделать вывод о том, находится ли маркетинговая деятельность вашей фирмы в сравнении с другими аналогичными фирмами лишь на несколько более низком уровне или же ваша фирма является некоторым исключением из общей картины. Такая информация может помочь в стратегическом планировании затрат на маркетинг в следующем году. Изменчивость можно определить как степень различий между отдельными значениями. Подобный смысл имеют также такие понятия, как разнообразие, неопределенность, рассеяние и разброс. Далее мы увидим, что существуют три разных способа описания степени изменчивости набора данных, причем каждый из них требует соответствующих числовых значений. 1. Стандартное отклонение (в русскоязычной литературе по статистике часто также используют термины “среднее квадратическое отклонение” или “среднее квадратичное отклонение") используют наиболее часто. Этот показатель описывает, насколько сильно результат наблюдений обычно отличается от среднего значения. При возведении стандартного отклонения в квадрат получаем дисперсию. 2. Размах легко вычисляется, однако дает несколько поверхностное представление об изменчивости данных и имеет ограниченное применение. Эта величина описывает пределы изменения данных в наборе и представляет собой расстояние между минимальным и максимальным значениями. 3. Коэффициент вариации обычно выбирается в качестве относительной (в противоположность абсолютной) меры изменчивости. Этот показатель используется достаточно часто. Он показывает, насколько сильно обычно отличается результат конкретного наблюдения от среднего значения, в процентном отношении к среднему; при этом используется отношение стандартного отклонения к среднему значению. Мы также рассмотрим, как влияет на изменчивость данных изменение шкалы измерения (например, переход от японской иены к долларам США или переход от количества единиц выпущенной продукции к денежной стоимости этой продукции).
Стандартное отклонение
Стандартное отклонение — это число, описывающее, насколько значения данных обычно отличаются от среднего. Понятие стандартного отклонения является очень важным в статистике, поскольку оно представляют собой основной инструмент определения степени случайности в изучаемой ситуации. В частности, этот показатель является мерой случайности отклонений отдельных значений от их среднего. Если все величины одинаковы, как, например, в приведенном ниже простом наборе данных 5,5; 5,5; 5,5; 5,5 то среднее будет иметь значение В реальной жизни большинство данных характеризуется большей или меньшей степенью изменчивости. Отдельные значения набора данных располагается на некотором расстоянии от среднего, а стандартное отклонение характеризует степень изменчивости. Рассмотрим теперь другой набор данных, которым присуща некоторая изменчивость: 43,0; 17,7; 8,7; -47,4 Эти числа являются значениями ставки доходности (например, 43%) акций четырех компаний (Maytag, Boston Scientific, Catalytica и Mitcham Industries), выбранных случайным образом (случайность обеспечивалась путем метания стрелы игры дарт в газетную страницу с котировками акций). Среднее значение в этом случае такое же, Таблица 5.1.1
Описанные выше расстояния от среднего значения называются отклонением, или разностью. Они показывают, насколько выше среднего значения (в случае положительной разности) или ниже среднего (если разность отрицательна) лежит каждое значение данных. Отклонения в свою очередь образуют набор данных, расположенных вокруг нуля, что похоже на исходный набор данных, значения в котором расположены вокруг среднего. В качестве обобщающей характеристики отклонений используют стандартное отклонение. Просто усреднить отклонения нельзя, поскольку часть из них окажется отрицательными, а часть — положительными, в результате чего результат такого усреднения всегда будет равен нулю и не будет содержать никакой дополнительной информации. Вместо этого используют стандартный прием, заключающийся в том, что каждое значение сначала возводят в квадрат, чтобы избавиться от знака “минус”, затем складывают, делят на n-1 и извлекают квадратный корень (это обратная операция по отношению к выполненному ранее возведению в квадрат). Путем алгебраических преобразований можно показать, что сумма отклонений от среднего для любого набора данных всегда будет равна нулю. Казалось бы, следует просто заменить знаки «минус» на «плюс» и затем провести усреднение. Однако несложно также показать, что такой простой метод не обеспечивает эффективного использования всей содержащейся в данных информации, если речь идет о нормальном распределении. Деление на n-1 вместо n (как это обычно делают при вычислении среднего значения) связано с поправкой, обусловленной тем фактом, что при работе с выборкой истинное значение среднего генеральной совокупности неизвестно. Можно также считать, что эта поправка обусловлена потерей при вычислении отклонений одной порции информации (или, как говорят в статистике, одной степени свободы). Потерянной является информация об истинных значениях данных (поскольку теперь, при работе с отклонениями, данные расположены не вокруг среднего, а вокруг нуля).
Изменчивость: изучение разнообразия
Одна из причин, по которым возникает необходимость в проведении статистического анализа, состоит в том, что данные изменчивы. Если бы данные не изменялись, то ответы на многие вопросы были бы просто очевидными и нам не нужно было бы обращаться к методам статистического анализа. Ситуация, в которой присутствует изменчивость, часто содержит риск, поскольку даже использование всей доступной информации не позволяет точно предугадать, что же произойдет в будущем. Для адекватной работы с риском необходимо понимать его природу и уметь измерять изменчивость (часто также используют термин “вариация”), которая является его следствием. Приведем несколько ситуаций, в которых изменчивость имеет важное значение. Случай первый. Рассмотрим изменчивость производительности труда работников. Совершенно очевидно, что эффективность работы отдела определяется общей производительностью труда всех его сотрудников. Однако любые усилия, направленные на повышение производительности труда, должны учитывать индивидуальные особенности работников. Например, некоторые программы повышения производительности труда могут быть ориентированы на всех работников, в то время как другие — уделять особое внимание самым “быстрым” или самым “медленным” из них. Определение изменчивости производительности труда дает возможность выявить разброс таких индивидуальных различий и получить полезную информацию для планирования мероприятий по повышению общей производительности труда. Случай второй. Фондовая биржа в среднем обеспечивает более высокую доходность вложенных средств, чем, например, фонды денежного рынка. Однако работа на фондовой бирже связана с большим риском, и инвестирование в акции может привести к реальным потерям. Таким образом, средняя, или “ожидаемая” доходность не отражает полностью всю картину. Мера изменчивости доходности отдельных инвестиций будет отражать уровень риска, сопряженного с каждым конкретным вложением средств. Случай третий. Предполагается, что вы сравниваете маркетинговые затраты своей фирмы с аналогичными затратами фирм, работающих в вашей отрасли промышленности, и обнаруживаете, что затраты вашей фирмы меньше затрат, типичных для данной отрасли. Для того чтобы оценить затраты на будущее, очень полезным может оказаться учет разброса соответствующих данных по отрасли. Найдя разность между значением затрат своей фирмы и средним значением по отрасли и сравнив полученную величину с мерой изменчивости затрат в отрасти, можно сделать вывод о том, находится ли маркетинговая деятельность вашей фирмы в сравнении с другими аналогичными фирмами лишь на несколько более низком уровне или же ваша фирма является некоторым исключением из общей картины. Такая информация может помочь в стратегическом планировании затрат на маркетинг в следующем году. Изменчивость можно определить как степень различий между отдельными значениями. Подобный смысл имеют также такие понятия, как разнообразие, неопределенность, рассеяние и разброс. Далее мы увидим, что существуют три разных способа описания степени изменчивости набора данных, причем каждый из них требует соответствующих числовых значений. 1. Стандартное отклонение (в русскоязычной литературе по статистике часто также используют термины “среднее квадратическое отклонение” или “среднее квадратичное отклонение") используют наиболее часто. Этот показатель описывает, насколько сильно результат наблюдений обычно отличается от среднего значения. При возведении стандартного отклонения в квадрат получаем дисперсию. 2. Размах легко вычисляется, однако дает несколько поверхностное представление об изменчивости данных и имеет ограниченное применение. Эта величина описывает пределы изменения данных в наборе и представляет собой расстояние между минимальным и максимальным значениями. 3. Коэффициент вариации обычно выбирается в качестве относительной (в противоположность абсолютной) меры изменчивости. Этот показатель используется достаточно часто. Он показывает, насколько сильно обычно отличается результат конкретного наблюдения от среднего значения, в процентном отношении к среднему; при этом используется отношение стандартного отклонения к среднему значению. Мы также рассмотрим, как влияет на изменчивость данных изменение шкалы измерения (например, переход от японской иены к долларам США или переход от количества единиц выпущенной продукции к денежной стоимости этой продукции).
Стандартное отклонение
Стандартное отклонение — это число, описывающее, насколько значения данных обычно отличаются от среднего. Понятие стандартного отклонения является очень важным в статистике, поскольку оно представляют собой основной инструмент определения степени случайности в изучаемой ситуации. В частности, этот показатель является мерой случайности отклонений отдельных значений от их среднего. Если все величины одинаковы, как, например, в приведенном ниже простом наборе данных 5,5; 5,5; 5,5; 5,5 то среднее будет иметь значение В реальной жизни большинство данных характеризуется большей или меньшей степенью изменчивости. Отдельные значения набора данных располагается на некотором расстоянии от среднего, а стандартное отклонение характеризует степень изменчивости. Рассмотрим теперь другой набор данных, которым присуща некоторая изменчивость: 43,0; 17,7; 8,7; -47,4 Эти числа являются значениями ставки доходности (например, 43%) акций четырех компаний (Maytag, Boston Scientific, Catalytica и Mitcham Industries), выбранных случайным образом (случайность обеспечивалась путем метания стрелы игры дарт в газетную страницу с котировками акций). Среднее значение в этом случае такое же, Таблица 5.1.1
Описанные выше расстояния от среднего значения называются отклонением, или разностью. Они показывают, насколько выше среднего значения (в случае положительной разности) или ниже среднего (если разность отрицательна) лежит каждое значение данных. Отклонения в свою очередь образуют набор данных, расположенных вокруг нуля, что похоже на исходный набор данных, значения в котором расположены вокруг среднего. В качестве обобщающей характеристики отклонений используют стандартное отклонение. Просто усреднить отклонения нельзя, поскольку часть из них окажется отрицательными, а часть — положительными, в результате чего результат такого усреднения всегда будет равен нулю и не будет содержать никакой дополнительной информации. Вместо этого используют стандартный прием, заключающийся в том, что каждое значение сначала возводят в квадрат, чтобы избавиться от знака “минус”, затем складывают, делят на n-1 и извлекают квадратный корень (это обратная операция по отношению к выполненному ранее возведению в квадрат). Путем алгебраических преобразований можно показать, что сумма отклонений от среднего для любого набора данных всегда будет равна нулю. Казалось бы, следует просто заменить знаки «минус» на «плюс» и затем провести усреднение. Однако несложно также показать, что такой простой метод не обеспечивает эффективного использования всей содержащейся в данных информации, если речь идет о нормальном распределении. Деление на n-1 вместо n (как это обычно делают при вычислении среднего значения) связано с поправкой, обусловленной тем фактом, что при работе с выборкой истинное значение среднего генеральной совокупности неизвестно. Можно также считать, что эта поправка обусловлена потерей при вычислении отклонений одной порции информации (или, как говорят в статистике, одной степени свободы). Потерянной является информация об истинных значениях данных (поскольку теперь, при работе с отклонениями, данные расположены не вокруг среднего, а вокруг нуля).
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.211 (0.007 с.) |

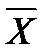 = 5,5, а стандартное отклонение составит S = 0. Последнее отражает тот факт, что в этом тривиальном наборе данные не подвержены изменчивости.
= 5,5, а стандартное отклонение составит S = 0. Последнее отражает тот факт, что в этом тривиальном наборе данные не подвержены изменчивости.


