
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этапы имитационного моделированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Имитационное моделирование как особая информационная технология состоит из следующих основных этапов. 1. Структурный анализ процессов. Проводится формализация структуры сложного реального процесса путем разложения его на подпроцессы, выполняющие определенные функции и имеющие взаимные функциональные связи согласно легенде, разработанной рабочей экспертной группой. Выявленные подпроцессы, в свою очередь, могут разделяться на другие функциональные подпроцессы. Структура общего моделируемого процесса может быть представлена в виде графа, имеющего иерархическую многослойную структуру. В результате появляется формализованное изображение имитационной модели в графическом виде. Экономические процессы содержат подпроцессы, не имеющие физической основы и протекающие виртуально, так как оперируют с информацией, деньгами, логикой, законами и их обработкой, поэтому структурный анализ является эффективным этапом при моделировании экономических процессов. На этом этапе описываются экзогенные переменные, т.е. те переменные, которые задаются вне модели, т.е. известны заранее. Ещё описываются параметры - это коэффициенты уравнений модели. Часто их не разделяют. Эндогенные переменные - это те переменные, кот. опред. в ходе расчетов по модели и не задаются в ней извне. 2. Формализованное описание модели. Графическое изображение модели, ф-ии, выполняемой каждым подпроцессом, условия взаимодействия всех подпроцессов и особенности поведения моделируемого процесса (временная, пространственная, финансовая динамики_ д.б. описаны на спец языке одним из способов: · Описание вручную на алгоритмическом языке, т.е. написание программы на языке програмирования. · Автоматизир описание с пом компьютерного графического конструктора. 3. Построение модели.
4. Проведение модельного эксперимента. Проводится оптимизация определенных параметров реального процесса. Этому должен предшествовать процесс, кот. называется планирование эксперимента. МЕТОД МОНТЕ-КАРЛО - Способ исследования поведения вероятностных систем экономических, технических и т.п. в условиях, когда неизвестны в полной мере внутренние взаимодействия в этих системах. Создателями метода статистических испытаний (метода Монте-Карло) считают американских математиков Д. Неймана и С. Улама. В 1944 году, в связи с работами по созданию атомной бомбы Нейман предложил широко использовать аппарат теории вероятностей для решения прикладных задач с помощью ЭВМ. Данный метод был назван так в честь города в округе Монако, из-за рулетки, простейшего генератора случайных чисел. Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались мало пригодными. Далее его влияние распространилось на широкий класс задач статистической физики, очень разных по своему содержанию. К разделам науки, где все в большей мере используется метод Монте-Карло, следует отнести задачи теории массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других. Метод Монте-Карло (или метод статистических испытаний) можно определить как метод моделирования случайной величины с целью вычисления характеристик их распределений. Суть состоит в том, что результат испытаний зависит от некоторой случайной величины, распределенной по заданному закону. Поэтому результат каждого отдельного испытания носит случайный характер. (Как правило, составляется программа для осуществления одного случайного испытания.) Проведя серию испытаний, получают выборку. Полученные статистические данные обрабатываются и представляются в виде численных оценок интересующих исследователя величин (характеристик системы). Т.е. испытание повторяется N раз, причем каждый опыт не зависит от остальных, и результаты всех опытов усредняются. Это значит, что число испытаний должно быть достаточно велико, поэтому метод существенно опирается на возможности компьютера. Теоретической основой метода Монте-Карло являются предельные теоремы теории вероятностей. Они гарантируют высокое качество статистических оценок при весьма большом числе испытаний. Метод статистических испытаний применим для исследования как стохастических, так и детерминированных систем. Практическая реализация метода Монте-Карло невозможна без использования компьютера. Можно проиллюстрировать метод статистических испытаний на простейшем примере: вычисление числа π как отношение площади 1/4 круга к площади всей картинки путем разбрасывания случайным образом точек по всему рисунку. Затем считается отношение попавших в круг точек ко всем точкам, и по этому отношению приблизительно определяется отношение площадей. Увеличением числа вбрасываемых точек можно более точно определить площадь круга, но это так же ведет и к увеличению времени вычислений. Точность вычислений очень сильно зависит от качества используемого генератора псевдослучайных чисел. Другими словами, точность тем выше, чем более равномерно случайные точки распределяются по единичному квадрату. p»4Sкр/Sкв (1) Подсчитаем число точек внутри квадрата и внутри четверти круга. Очевидно, что их отношение будет приближенно равно отношению площадей этих фигур, так как попадание капель в различные места чертежа равновероятно. Пусть Nкр - число капель в круге,Nкв –число капель в квадрате, тогда
Каждому точке поставим в соответствие два случайных числа, характеризующих его положение вдоль осей Ох и Оу (см. рис. 2). Если окажется, что для точки (хi,уi) выполняется неравенство хi2+уi2>1, то, значит, она лежит вне круга. Если хi2 +уi2 Ј 1, то точка лежит внутри круга.
Для подсчета значения p воспользуемся формулой (2). Ошибка вычислений по этому методу, как правило пропорциональна Базовый датчик Моделирование случайных элементов в системах является одной из самых главных, базовых задач математического моделирования. Любая случайная величина или процесс X может моделироваться следующим образом:
Базовый датчик выдает независимые равномерно распределенные случайные величины: 1. непрерывные в [0,1); 2. дискретные в Типы базовых датчиков: 1. физические (любой физический шум) – не используются, т.к. характеристики нестабильны и реализацию повторить нельзя; 2. псевдослучайные – строятся на основе детерминированного алгоритма, но полученные результаты неотличимы от случайных. Псевдослучайные базовые датчики строятся по модели Требования к базовым датчикам и их проверка Отрезок апериодичности Периодом T и длиной отрезка апериодичности датчика называются наименьшие из величин, удовлетворяющие
Чем больше T и L, тем лучше датчик (особенно L). Как определить их: 1. Берем V – достаточно большое число (обычно 2. Генерируем 3. Генерируем 4. Генерируем Равномерность Должно быть Проверка: 1. Берем 2. Находим 3. Для каждого числа
и заполняем массив 4. По значениям этого массива строим гистограмму (для наглядности). 5. Используем критерий
Выбираем уровень значимости Некоррелированность 1. Генерируем 2. Вычисляем 3. Вычисляем 4. Проверяем для всех k
Если да, то «данные эксперимента не противоречат гипотезе о равномерности случайных чисел», иначе – «противоречат». Здесь 4. Простейшие проверки Подходят для любой непрерывной случайной величины. 1. Математическое ожидание: 2. Дисперсия:
Мультипликативный конгруэнтный метод (метод вычетов) В основе лежит следующее рекуррентное соотношение:
Для 32-разрядной:
Генерация случайных событий 1. Пусть имеется некоторое случайное событие А, наступающее с вероятностью р(А). Тогда
2. Полная группа попарно несовместимых событий
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.111 (0.007 с.) |

 p»4Nкр/Nкв (2)
p»4Nкр/Nкв (2)

 , где D – некоторая постоянная, а N – число испытаний. В этом примере
, где D – некоторая постоянная, а N – число испытаний. В этом примере  . Из этой формулы видно, что для того, чтобы уменьшить ошибку в 10 раз, т.е. получить ещё один верный десятичный знак, нужно увеличить N, т.е. объём работы, в 100 раз (см. таблицу с результатами испытаний).
. Из этой формулы видно, что для того, чтобы уменьшить ошибку в 10 раз, т.е. получить ещё один верный десятичный знак, нужно увеличить N, т.е. объём работы, в 100 раз (см. таблицу с результатами испытаний).
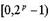
 при заданном
при заданном 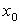



 и проверяем
и проверяем  ,запоминая.
,запоминая. и проверяем
и проверяем 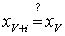 . Если нет для
. Если нет для  , то
, то 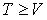 и
и  . Иначе запоминаем
. Иначе запоминаем  , для которого
, для которого  , и находим следующий
, и находим следующий  , для которого
, для которого 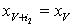 (если нужно, генерируются дополнительные величины). Тогда
(если нужно, генерируются дополнительные величины). Тогда 
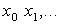 и
и 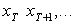 и ищем первое совпадение
и ищем первое совпадение  . Тогда
. Тогда 
 для
для 
 и генерируем
и генерируем 
 и разбиваем отрезок [0,1) на k равных частей (длиной
и разбиваем отрезок [0,1) на k равных частей (длиной  )
) определяем, в какой интервал оно попало:
определяем, в какой интервал оно попало:
 :
: 

 .
. (обычно 5%), а число степеней свободы
(обычно 5%), а число степеней свободы  . В таблицах
. В таблицах 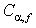 и проверяем: если
и проверяем: если  ,то «данные эксперимента не противоречат гипотезе о равномерности случайных чисел», иначе – «противоречат».
,то «данные эксперимента не противоречат гипотезе о равномерности случайных чисел», иначе – «противоречат».
 ,
,  (можно и больше).
(можно и больше).
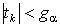
 берется из таблиц
берется из таблиц 



 – множитель, M – модуль,
– множитель, M – модуль,  – стартовое значение. Рекомендуемые значения для 64-разрядной сетки:
– стартовое значение. Рекомендуемые значения для 64-разрядной сетки:



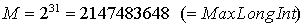

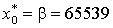

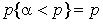 (
( ,где
,где 
 . Пусть
. Пусть  Идея:
Идея:




