Алгоритм построения таблицы истинности сложного высказывания

 

Вычислить количество строк и столбцов таблицы истинности.

Пусть сложное высказывание состоит из n простых.

Количество строк: 2ⁿ +2 (2-строки заголовка).

Количество столбцов: сумма количества переменных (n) + количества логических операций, входящих в сложное высказывание.

 

Начертить таблицу и заполнить заголовок.

Первая строка – номера столбцов.

Вторая строка - промежуточные формулы и соответствующие им условные записи операций над значениями пар столбцов, содержащие номера этих столбцов.

 

Заполнить первые n столбцов.

Для n=3 количество строк со значениями переменных равно 8.

8:2=4: в 1-м столбце чередуем 4 нуля и 4 единицы.

4:2=2: во 2-м столбце чередуем 2 нуля и 2 единицы.

2:2=1: в 3-м столбце чередуем 1 ноль и 1 единицу.

Таким образом, все возможные комбинации значений переменных учтены и никакие две не совпадают.

 

Заполнить остальные столбцы.

Остальные столбцы заполняем в соответствии с таблицами истинности соответствующих логических операций, причем при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, расположенных левее заполняемого.

 

Пример

Е = (КUС) & С?К.

 

1. Определим количество строк и столбцов в таблице истинности.

Количество строк: 2^{2 +}2=6;

Количество столбцов: 2+4=6.

2. Начертим таблицу и заполним ее в соответствии с определениями логических операций последовательно по столбцам.

 

К	С	С (2)	К U С (1) U(2)	(К U С) & С (4) & (3)	(К U С) & С?К (5)?(1)

 

Вывод: мы получили в последнем столбце все единицы. Это означает, что значение сложного высказывания истинно при любых значениях простых высказываний К и С.

 

Логические элементы и схемы. Типовые логические устройства компьютера: полусумматор, сумматор, триг­геры, регистры.

 

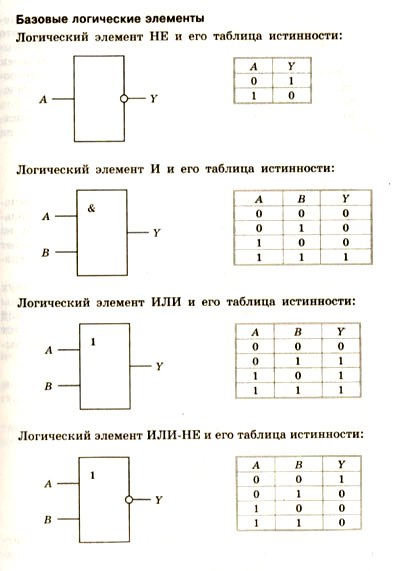
Работа компьютера состоит в операциях над двоичными кодами и пересылке этой информации по линиям связи. Средством обработки двоичных сигналов в компьютере яв­ляются логические элементы. Причем, для реализации лю­бых логических операций над двоичными сигналами доста­точно элементов трех типов, реализующих три основные ло­гические операции — И, ИЛИ, НЕ. Логический элемент — это электронная схема с одним или несколькими входами и одним выходом, через которые проходят электрические сиг­налы, представляющие цифры 1 и 0; на выходе логический элемент выдает значение логического произведения, логиче­ской суммы или отрицания.

 

Базовые логические элементы

Так как сигнал, выработанный одним логическим эле­ментом, можно подавать на вход другого элемента, то это дает возможность образовывать схемы из отдельных логи­ческих элементов, которые называются функциональными схемами. Из отдельных логических элементов можно со­здать функциональную схему арифметического назначе­ния.

Устройства компьютера (сумматор в процессоре, регист­ры, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.

 

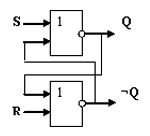
Типовые логические устройства

Триггер

Для хранения информации в оперативной памяти компь­ютера, а также во внутренних регистрах процессора исполь­зуются триггеры. Триггер может находиться в одном из двух устойчивых состояний (одно из которых обозначает ноль, а другое — единицу), что позволяет запоминать, хра­нить и считывать 1 бит информации.

Самый простой триггер — RS-триггер. Он состоит из двух элементов ИЛИ-НЕ, входы и выходы которых соединены кольцом: выход первого соединен со входом второго и выход второго — со входом первого. Триггер имеет два входа S (от англ. set — установка) и R (от англ. reset — сброс) и два вы­хода Q (прямой) и Q (инверсный).

 

Логическая схема RS -триггера

 

Если на входы поступают сигналы R = 0 и S = 0, то триг­гер находится в режиме хранения, на выходах Q и Q сохра­няются установленные ранее значения.

Если на установочный вход S поступает на короткое время сигнал 1, то триггер переходит в состояние 1 и после того, как сигнал на входе S станет равен 0, триггер будет со­хранять это состояние, т. е. будет хранить 1. При подаче 1 на вход R триггер перейдет в состояние 0. Подача на оба вхо­да S и R логической единицы может привести к неоднознач­ному результату, поэтому такая комбинация входных сигна­лов запрещена

 

Входы	Состояние Q
S	R
		Q	Хранение
			Установка 1
			Установка 0
		Недопустимо	Запрещенная комбинация

 

Сумматоры

Сумматор — это вычислительная схема, выполняющая процедуру сложения поступающих на ее вход двоичных ко­дов.

По числу входов различают полусумматоры, одноразряд­ные сумматоры (ОС) и многоразрядные сумматоры.

Рассмотрим построение схемы одноразрядного полусум­матора, предназначенного для сложения двух двоичных чи­сел в одном разряде.

Составим таблицу логических значений для сумматора, где А, В — слагаемые, Р и Y — перенос и цифра разряда для суммы соответственно:

 

Входы	Выходы
A	B	P	Y

 

Заметим, что Р — это функция, реализующая операцию конъюнкции двух переменных A и В, а Y - отрицание опе­рации эквивалентности:

Р = А & В;

Y = (A v В) & (А & В).

 

На основе полученных логических функций можно по­строить схему полусумматора. Схема требует два логиче­ских элемента И, один логический элемент ИЛИ, один логи­ческий элемент НЕ.

Эта схема называется полусумматором, так как в ней от­сутствует третий вход — перенос из предыдущего разряда.

Схема полного одноразрядного сумматора должна содер­жать три входа: два слагаемых одного разряда и перенос из предыдущего разряда; и два выхода: сумму в данном разря­де и перенос в следующий разряд.

Составим таблицу логических значений для одноразряд­ного сумматора, где А, В — слагаемые, P0— перенос из пре­дыдущего разряда, P и Y — перенос в следующий разряд и цифра разряда для суммы соответственно. В таблице будет 8 строк, так как имеется 3 входа:

 

Входы	Выходы
А	B	Р0	Р	Y

 

Схема одноразрядного сумматора:

 

Регистр

Триггер запоминает один разряд двоичного числа. Для запоминания n-разрядного двоичного числа необходимо n соединенных между собой триггеров. Получаем n-разряд­ный регистр.

 

Информационные (нематериальные) модели. Моделиро­вание как метод познания. Назначение и виды информа­ционных моделей. Основные этапы компьютерного моде­лирования.