Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применяя формулу (1), получимСодержание книги Поиск на нашем сайте
Следовательно,
4) Площадь грани А1 А2 А3 равна половине площади параллелограмма, построенного на векторах Координаты вектора
5) Объем пирамиды V в шесть раз меньше объема параллелепипеда V1, построенного на трех некомпланарных векторах, и равен абсолютной величине их смешанного произведения. Вычислим смешанное произведение
Следовательно, V1 параллелепипеда равен 144 куб. ед., а объем заданной пирамиды V = 144/6 =24 куб. ед. 6) Уравнение прямой, проходящей через две заданные точки А1 (х1, y1, z1) и А2 (х2, y2, z2) имеет вид
Подставив в (7) координаты точек А1 и А2, получим
7) Уравнение плоскости А1А2А3 – это уравнение грани А1А2А3, которое найдено в п.3:
А1А2А3 : 2х – у – 2z – 3 = 0
8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3 – это перпендикуляр А4Д. Каноническое уравнение прямой в пространстве имеет вид
где х0, у0, z0 – координаты точки, через которую проходит прямая (8), а m, n, p – направляющие коэффициенты этой прямой. По условию прямая проходит через точку А4( 0; 1; 4) и перпендикулярные грани А!А2А3 для которой
Пример 3. Линия задана уравнением
Решение. 1) Построим линию по точкам от φ = 0 до φ = 2π, придавая φ значения через промежуток
Составим таблицу:
Построим полученные точки в полярной системе координат (рис. 1).
Рис. 1. 2) Найдем уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абцисс ОХ – с полярной осью р. Для этого воспользуемся формулами перехода к прямоугольной декартовой системе координат х = rcosφ, y = rsinφ, откуда r2=x2+y2,
Возведем в квадрат обе части последнего равенства:
Разделим обе части последнего уравнения на 24336:
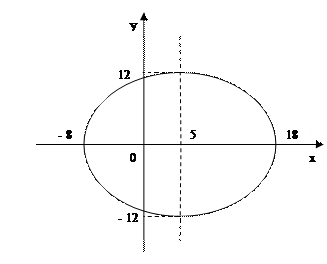
Полученное уравнение – уравнение эллипса с центром в точке А (5; 0), полуоси которого
Проверим r(-φ), зная, что cosφ=cos(-φ)
Так как r(-φ)=r(φ), то данная линия будетсимметрична относительно полярной оси р и достаточно найти r(φ) для угловот φ=0 до φ=π.
Пример 4. Данную систему уравнений:
решить по формулам Крамера (через определитель) и средствами матричного исчисления (с помощью обратной матрицы). Обозначим через А матрицу коэффициентов при неизвестных; Х – м-цу - столбец неизвестных х1, х2, х3; В – м-цу – столбец свободных членов:
С учетом этих обозначений данная система уравнений примет следующую матричную форму:
Если матрица А – невырожденная (ее определитель
но
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо выписать обратную матрицу А-1. Пусть имеем невырожденную матрицу
где Mij – минор (определитель) второго порядка, полученный вычеркиванием i –й строки и j – го столбца в определителе матрицы А. Вычислим определитель Δ и алгебраические дополнения Aij элементов матрицы А.
тогда
По формуле (2) находим решение данной системы уравнений в матричной форме:
отсюда х1=3, х2=0, х3=-2. Если определитель системы уравнений
Формулы (3) называются формулами Крамера, где Δхi получается заменой i-го столбца в главном определителе Δ столбцом свободных членов. Если определитель системы Δ=0 и по крайней мере один из определителей Определитель данной системы Вычислим вспомогательные определители:
Применяя формулы (3), находим:
ΙΙ. Введение в математический анализ Пример 1. Дано комплексное число 2) записать число а в алгебраической и тригонометрической формах; 3) найти все корни уравнения z3 + a = 0, Решение. 1) Комплексным числом называется выражение
z = a + вi (1)
где а и в, действительные числа, а i – мнимая единица, которая определяется равенством i2=-1,
Таким образом, имеем: Всякое комплексное число z = a + вi можно изобразить на плоскости хОу, в виде точки А(а; в); Точками, лежащими на оси Ох, соответствуют действительные числа (в=0). Если же точка расположена на оси Оу, то она изображает чисто мнимое число, так как а=0. Поэтому ось Оу называют осью мнимых чисел или мнимой осью, а ось Ох – действительной осью.
Рис 1.
Исходя из рис.2 a = r cosφ, в = r sinφ, где r и φ – полярные координаты точки А(а; в). Тогда тригонометрическая форма записи числа запишется в следующем виде:
Величины r и φ выражаются через а и в формулами
где Для данного комплексного числа
Таким образом, 2) Представим уравнение Корень n – ой степени из комплексного числа z = r (cos φ + i sin φ) имеет n различных значений, которые находятся по формуле
где
Запишем выражение - Можно считать, что угол φ принадлежит 3-й четверти; φ = 270˚-α, где α - угол в 1-ой координатной четверти. Имеем угол Итак,
Придавая k последовательно значения 0, 1, 2, получим соответственно числа z1, z2, z0.
Пример 2. Если известен график функции у = f(x), то график функции вида у = kf(mx + b) + a можно построить последовательным преобразованием графика функции у = f(x). Покажем, например, как с помощью таких преобразований можно построить график функции у = -2sin(2x + 2), исходя из известного графика функции у = sinx. От функции у = sinx к функции у = - 2sin(2x + 2) можно перейти с помощью следующей цепочки преобразований:
y1 = sin2x1, y2 = - 2sin2x2, Y = - 2sin2(X + 1) = - 2sin(2X + 2). Геометрически это приводит к следующим построениям (рис.2): 1) Строим одну волну синусоиды у = sinx; 2) Отмечаем на синусоиде несколько точек и уменьшаем в два раза их абсциссы, не изменяя ординат; таким образом мы отображаем точку (х; у) и точку (х1; у1), где х1 = х/2, у1 = у. Соединив полученные точки плавной линией, получим график функции у1 = sin2x1, являющийся результатом «сжатия» графика функции у = sinx к оси Оу в два раза.
3) Увеличиваем ординаты точек, построенных в предыдущем пункте в два раза, а затем меняем их знаки на противоположные, не изменяя абсцисс; таким образом отображаем точку (х1;у1) в точку (х2; у2), где у2 = - 2у1, х2 = х1. Соединив полученные точки плавной линией, получим график функции у2 = - 2sin2x2, являющейся результатом «растяжения» графика функции у1 = sin2x1 от оси Ох в два раза с последующим зеркальным отражением графика от оси Ох. 4) Переносим точки, построенные в предыдущем пункте, на –1 в направлении оси Ох (т.е. на единицу влево); таким образом мы отображаем точку (х2; у2) в точку (Х; Y), где Х = х2 - 1, Y = у2. Соединив полученные точки плавной линией, получим график функции Y = -2sin 2(X + 1) = - 2sin (2X + 2), являющийся результатом «сдвига» графика функции у2 = - 2sin 2х2 на –1 в направлении оси Ох. Искомый график функции у = - 2sin (2x +2) построен.
Рис. 2.
Пример 3. Найти пределы функции не пользуясь правилом Лопиталя:
Решение. а) Под знаком предела имеется дробная рациональная функция и при х→∞ получается неопределенность вида
б) Непосредственная подстановка предельного значения аргумента х=2 приводит к неопределенности вида
в) Непосредственная подстановка предельного значения аргумента х=0 приводит к неопределенности Так как при х→∞ ln(1 + x)~ x, tg x ~ x, то ln(1 + 3x sin x) ~3x sin x, tg x2~ x2 и (используя 1-ый замечательный предел г) При х→∞ основание
Представим основание в виде суммы: единицы и некоторой бесконечно малой величины:
Тогда
Положим х – 2 = 3у; при х → ∞ переменная у → ∞. Выразим показатель степени через новую переменную у. Так как х = 3у + 2, то 2х -1 = 2(3у + 2) – 1 = 6у + 3. Таким образом,
Пример 4. Дана функция у =161/(2+х). Требуется: 1) установить, является ли данная функция непрерывной или разрывной при значениях аргумента х1=-2, х2=0; 2) в случае разрыва функции найти ее пределы в точке разрыва справа и слева; 3) сделать схематический чертеж. Решение. Если ищется предел функции у=f(х) при условии, что аргумент х, стремясь к своему предельному значению а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним (левым) пределом данной функции в точке х = а и условно обозначается так:
Если ищется предел функции у=f(х) при условии, что аргумент х, стремясь к своему предельному значению а, может принимать только такие значения, которые больше а, то этот предел если он существует, называется правосторонним (правым) пределом данной функции в точке х = а и условно обозначается так:
Функция у = f(х) непрерывна в точке х = а, если выполнимы следующие условия: 1) функция у = f(х) определена не только в точке а, но и в некотором интервале, содержащем эту точку; 2) функция у = f(х) имеет при х→а конечные и равные между собой односторонние пределы; 3) односторонние пределы при х → а совпадают со значением функции в точке а, т.е. Если для данной функция у = f(х) в данной точке х = а хотя бы одно из перечисленных условий не выполняется, то функция называется разрывной в точке х = а. Разрыв функция у = f(х) в точке х = а называется разрывом первого рода, если существуют конечные односторонние пределы Если же хотя бы один из односторонних пределов не существует, то разрыв в точке х = а называется разрывом второго рода. При х = -2, данная функция не существует: в этой точке функция терпит разрыв. Определим односторонние пределы функции при х = -2 слева и справа:
Таким образом, данная функция при х = -2 имеет разрыв второго рода. При х = 0 функция непрерывна, т.к. выполняются все три условные непрерывности функции. Данная функция является показательной. Прямая х = -2 – вертикальная асимптота графика функции. Множество значений функции – множество всех положительных чисел. у = 1 – горизонтальная асимптота, т.к. Чтобы построить функцию
График функции показан на рис. 3.
Рис. 3.
Пример 5. Задана функция y = f (х) различными аналитическими выражениями для различных областей изменения аргумента х:
Найти: 1) точки разрыва функции, если они существуют; 2)предел функции у при приближении аргумента х к точке разрыва слева и справа; 3)найти скачок функции в точке разрыва. Решение. Данная функция определена и непрерывна в интервалах (-∞; 0), (0; π) и (π; + ∞). При х = 0 и х = π меняется аналитическое выражение функции и только в этих точках функция может иметь разрыв. Определим односторонние пределы в точке х = 0;
Так как односторонние пределы функции у в точке х = 0 не равны между собой, то в этой точке функция имеет разрыв первого рода. Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями. Следовательно, в точке х = 0 скачок функции Δ=|1 - 0|=1. Определим односторонние пределы в точке х = π:
Односторонние пределы совпадают и функция в этой точке непрерывна. График функции показан на рис. 4.
Рис. 4.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.106.9 (0.012 с.) |

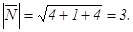

 и
и  . Обозначим через вектор
. Обозначим через вектор  векторное произведение векторов
векторное произведение векторов  , тогда площадь параллелограмма
, тогда площадь параллелограмма 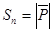 , а площадь грани
, а площадь грани 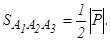
 найдем по формуле (3):
найдем по формуле (3):
 (11; 2; 10)
(11; 2; 10)

 кв. ед.
кв. ед. :
:
 (7)
(7)
 (8)
(8) (2; -1; -2), т.е. подставив эти данные в формулу (8), получаем
(2; -1; -2), т.е. подставив эти данные в формулу (8), получаем - уравнение высоты А4Д
- уравнение высоты А4Д в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой ситеме координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой ситеме координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия. .
.














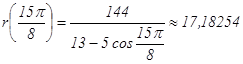
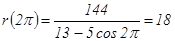





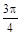









 тогда подставим эти формулы в данное уравнение
тогда подставим эти формулы в данное уравнение 

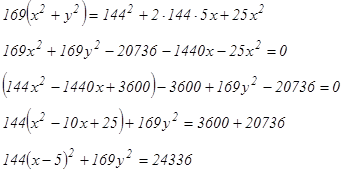
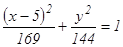

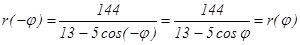

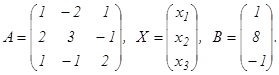
 (1)
(1) ), то она имеет обратную матрицу А-1. умножив обе части уравнения (1) на А-1, получим:
), то она имеет обратную матрицу А-1. умножив обе части уравнения (1) на А-1, получим: ,
, - единичная матрица, а ЕХ = Х, поэтому
- единичная матрица, а ЕХ = Х, поэтому (2)
(2) и ее определитель равен Δ, тогда
и ее определитель равен Δ, тогда  где Aij (i = 1,2,3; j = 1,2,3) – алгебраическое дополнение элемента aij в определителе матрицы А и
где Aij (i = 1,2,3; j = 1,2,3) – алгебраическое дополнение элемента aij в определителе матрицы А и 

 следовательно матрица А невырожденная и имеет обратную матрицу А -1.
следовательно матрица А невырожденная и имеет обратную матрицу А -1.


 (3)
(3)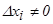 , то такая система уравнений не имеет решения. Если же Δ=0 и все Δхi=0, то данная система уравнений либо не имеет решения, либо имеет бесчисленное множество решений.
, то такая система уравнений не имеет решения. Если же Δ=0 и все Δхi=0, то данная система уравнений либо не имеет решения, либо имеет бесчисленное множество решений. .
.

 , требуется:
, требуется: ; а – действительная часть числа z, в – мнимая часть числа z. Равенство (1) называется алгебраической формой записи. Числа а + вi и а – вi, отличающиеся только знаком мнимой части, называются сопряженными комплексными числами. Умножим число а на множитель, сопряженным знаменателем:
; а – действительная часть числа z, в – мнимая часть числа z. Равенство (1) называется алгебраической формой записи. Числа а + вi и а – вi, отличающиеся только знаком мнимой части, называются сопряженными комплексными числами. Умножим число а на множитель, сопряженным знаменателем: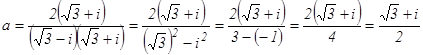
 - алгебраическая форма записи комплексного числа а.
- алгебраическая форма записи комплексного числа а. - начало его в точке О(0; 0), а конец в точке А(а; в).
- начало его в точке О(0; 0), а конец в точке А(а; в).
 или
или 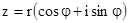 (2)
(2)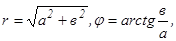
 - модуль, φ = arg z – аргумент комплексного числа z, который определяется с точностью до 2πk, k = 0,
- модуль, φ = arg z – аргумент комплексного числа z, который определяется с точностью до 2πk, k = 0,  1,
1, 
 - тригонометрическая форма записи комплексного числа.
- тригонометрическая форма записи комплексного числа.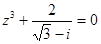 в виде
в виде  или
или  тогда
тогда  , т.е. задача сводится к вычислению всех значений
, т.е. задача сводится к вычислению всех значений 
 (3)
(3) - арифметическое значение корня, а число k пробегает значения 0, 1, 2, …, n - 1.
- арифметическое значение корня, а число k пробегает значения 0, 1, 2, …, n - 1. в виде
в виде  где
где 

 тогда
тогда 

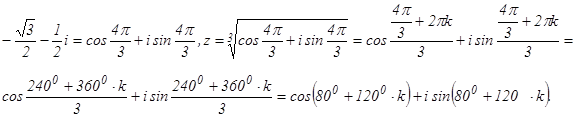



 .
.

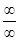 . Чтобы найти предел дробной рациональной функции
. Чтобы найти предел дробной рациональной функции  при х→∞, необходимо предварительно числитель и знаменатель дроби разделить на хn, где n – наивысшая степень многочленов Р(х) и Q(x). Разделим числитель и знаменатель данной дроби на х2 и применим основные теоремы о пределах и свойствах бесконечно малых величин:
при х→∞, необходимо предварительно числитель и знаменатель дроби разделить на хn, где n – наивысшая степень многочленов Р(х) и Q(x). Разделим числитель и знаменатель данной дроби на х2 и применим основные теоремы о пределах и свойствах бесконечно малых величин:
 . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму
. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму 

 . Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной.
. Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной.

 ).
). стремится к 1, а показатель степени (2х – 1)→∞. Следовательно, имеем неопределенность вида 1∞. Для ее раскрытия будем использовать II замечательный предел
стремится к 1, а показатель степени (2х – 1)→∞. Следовательно, имеем неопределенность вида 1∞. Для ее раскрытия будем использовать II замечательный предел 
 .
. .
.



 причем не все три числа f(a), f(a-0) и f(a+0) равны между собой.
причем не все три числа f(a), f(a-0) и f(a+0) равны между собой.
 а
а 

 и
и 
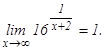
 , составим следующую таблицу:
, составим следующую таблицу: