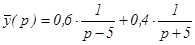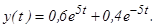Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы операционного исчисленияСодержание книги Поиск на нашем сайте
Пусть функция f(x) обладает следующими свойствами: 10. f(x) ≡0 при t < 0. 20. |f(x)| < МеSot при t > 0, где М > 0 и S0 – некоторые действительные постоянные. 30. На любом конечном отрезке [а, в] положительной полуоси Ot функция f(x) удовлетворяет условием Дирихле, т.е.: а) ограниченна; б) либо непрерывна, либо имеет лишь конечное число точек разрыва I рода; в) имеет конечное число экстремумов. Такие функции в операционном исчислении называются изображаемыми по Лапласу, или оригиналами. Пусть р = α + βi - комплексный параметр. При сформированных условиях интеграл
Этот интеграл называется интегралом Лапласа, а определяемая им функция комплексного аргумента р называется преобразованием Лапласа от функции f(t) или лапласовым изображением f(t) или просто изображением f(t).
Таблица изображений основных элементарных функций
Тот факт, что функция Если дано линейное дифференцированное уравнение n-го порядка с постоянными коэффициентами y(n) + a1y(n-1) +…+ any = f(t),
правая часть которого f(t) является оригиналом, то и решение этого уравнения, удовлетворяющее произвольным начальным условиям вида:
y (0) = y0, у΄(0) = y΄0, y΄΄=y0΄΄, …,y(n-1)(0) = y(n-1)0
(т.е. решение задачи Коши, поставленной для этого уравнения, с начальными условиями при t = 0, служит оригиналом. Обозначая изображение этого решения через Пусть оригинал f(t) дифференцируем n раз и его производные до n-го порядка в свою очередь являются оригиналами. Тогда справедлива теорема дифференцирования оригинала: если f(k)(t) В частности: f΄ f΄΄(t) f΄΄΄(t) Пример 1. Решить дифференциальное уравнение
y΄΄΄-6y΄΄+11y΄-6y=0, если у(0) = 0, у΄(0) = 1, у΄΄(0) = 0. Решение. Переходя к изображениям по теореме дифференцирования оригинала, получим:
Используем элементарные приемы для разложения этой дроби на сумму, таких простейших дробей, оригиналы которых известны:
Полагая р =1, находим –5 = 2 А, откуда А = -5/2. Полагая р =2, находим –4 = - В, откуда В = 4. При р = 3, находим –3 = 2 С, откуда С = -3/2.
Следовательно,
Отсюда, используя формулу (3) таблицы изображений, находим:
Пример 2. Решить систему уравнений: Решение. Перейдем к изображениям:
х΄
Система уравнений примет вид:
Из первого уравнения системы выразим
Выразим из 2-го уравнения
Осталось найти оригинал для
Полагая р =-1 получаем –8 = 4 В, откуда В= -2. Полагая р = 0, получаем 2 = -3 А, откуда А =- Полагая р = 3, получаем 32 = 12 С, откуда С = Следовательно:
Тогда Аналогично поступим с дробью для отыскивания оригинала для
При р = -1, 8 = 4 В, откуда В = 2. При р = 0, -1 = -3 А, откуда А = При р = 3, получаем 32 = 12 С, откуда С = Следовательно:
Тогда
Пример 3. Решить дифференциальное уравнение методом операционного исчисления
у΄΄-2у΄-3у = е3t, если у(0) = 0, у΄(0) = 0. Решение Перейдем к изображениям:
y΄΄ y΄ y е3t
или, учитывая начальные условия:
квадратный трехчлен р2- 2р – 3 можно разложить на два множителя, так как его корни р1= 3, р2 = -1: р2 – 2р – 3 = (р -3)(р+1). Окончательно имеем:
Полагая р = -1, получаем 1 = 16 С, т.е. При р = 3, имеем 1 = 4 А, т.е. Сравнивая коэффициенты при р2, получим О = В +С, т. е.
откуда, используя таблицу изображений, находим искомый оригинал и решение данного дифференциального уравнения:
или
Пример 4. Решить систему уравнений: Решение. Перейдя к изображениям имеем:
Из 1-го уравнения системы выразим
Из 2-го уравнения системы выразим
Таким образом:
Таким образом:
Разложив, полученные дроби на простейшие, по таблице изображений найдем оригинал:
При р = 5: 12 = 10А, А = 1, 2. При р =5: 6 = 10С, С = 0,6. При р = -5: 2 =-10В, В = -0,2. При р = -5: -4 = -10Д, Д = 0,4.
Следовательно,
Откуда
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.006 с.) |

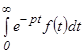 сходится и является функцией от р.
сходится и является функцией от р.
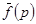
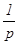

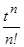
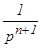
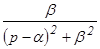
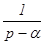


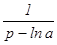

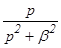
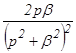
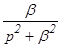
 является изображением оригинала f(t), обозначается следовательно символом
является изображением оригинала f(t), обозначается следовательно символом 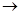 f(t).
f(t).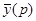 , находим изображение левой части исходного дифференцированного уравнения и, приравнивая его к изображению функции f(t),приходим к так называемому изображающему уравнению, которое всегда является линейным алгебраическим уравнением относительно
, находим изображение левой части исходного дифференцированного уравнения и, приравнивая его к изображению функции f(t),приходим к так называемому изображающему уравнению, которое всегда является линейным алгебраическим уравнением относительно  f(t), то
f(t), то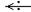 pk
pk 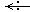 p ·
p · 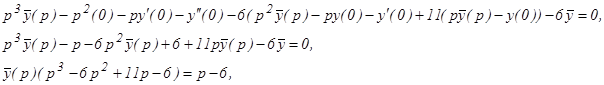
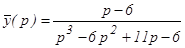 или
или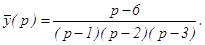
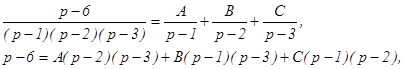
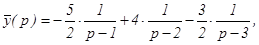
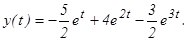
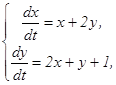 если х(0) =0, у (0) = 5.
если х(0) =0, у (0) = 5.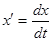
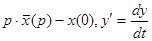
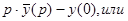
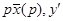
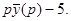
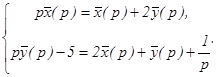
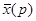 , подставим во 2-ое уравнение:
, подставим во 2-ое уравнение:
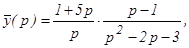 или
или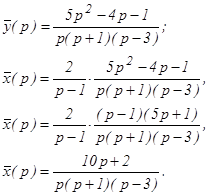


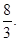
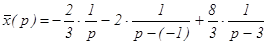 .
.

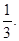
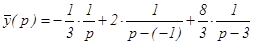
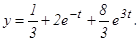
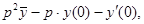

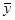
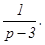 Тогда данное дифференциальное уравнение примет вид:
Тогда данное дифференциальное уравнение примет вид:
 откуда
откуда
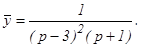 Осталось найти оригинал данной функции. Разложим полученную рациональную дробь на простейшие дроби:
Осталось найти оригинал данной функции. Разложим полученную рациональную дробь на простейшие дроби: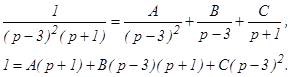
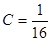 ;
;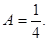
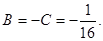 Следовательно,
Следовательно,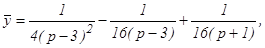
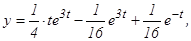
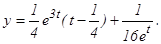
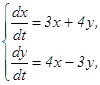 если х(0) = у (0) =1.
если х(0) = у (0) =1.
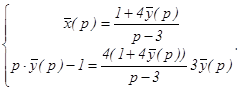
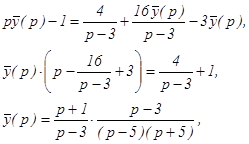
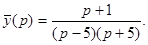

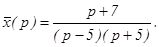

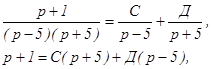
 и
и