
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистических гипотезСодержание книги
Поиск на нашем сайте
Практическое занятие 5 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ 1. Оценка достоверности разности средних. 1 2. Оценка достоверности средней разности. 5 3. Критерий c 2 как критерий согласия. 9 4. Критерий c 2 как критерий независимости. 24 5. Критерий c 2 как критерий однородности. 30
Оценка достоверности разности средних
Гипотеза о разности двух средних исходит из предположения, что независимые выборки взяты из одной нормально распределенной совокупности и различия между средними возникли случайно. Чтобы проверить гипотезу, необходимо найти фактическое нормированное отклонение и сравнить его с табличным. Если фактическое значение нормированного отклонения меньше табличного, то гипотеза подтверждается, то есть разница между средними недостоверна и различия между ними носят случайный характер. Если же фактическое значение нормированного отклонения больше табличного, следовательно, гипотеза опровергается, то есть разница между средними достоверна и различия между ними носят систематический характер. Фактическое нормированное отклонение определяют как отношение случайной ошибки к средней ошибке разности двух выборочных средних:
где
Табличное нормированное отклонение tтабл определяют по таблицам распределения Стьюдента исходя из принятого доверительного уровня вероятности суждения β (или уровня значимости a = 1 - β) и числа степеней свободы вариации n. Число степеней свободы вариации для первой и второй выборок соответственно равны В случае определения достоверности разности средних в больших выборках вместо t -критерия Стьюдента можно применять t -критерий нормального распределения. При этом число степеней свободы вариации не учитывается. Зная среднюю ошибку и табличное нормированное отклонение, можно определить предельную ошибку разности средних:
Сравнение предельной ошибки и разности средних также позволяет сделать вывод о достоверности разности средних. Если предельная ошибка меньше разности средних, то разность средних достоверна, если больше - нет.
Рассмотрим методику оценки достоверности разности средних. Пример. Имеются данные о продолжительности отела по двум группам коров в боксах-денниках и стойлах (табл. 5.1). Данные наблюдений по опытной и контрольной группам независимы. Т а б л и ц а 5.1 Название показателей, выводимых с помощью надстройки Анализ данных
Содержание жира в молоке
Требуется определить существенность различий между содержанием жира в молоке коров и их матерей при уровне вероятности суждения 0,99. Так как содержание жира в молоке дочерей и матерей зависимы между собой, то оценке подвергается средняя разность. Среднее содержание жира в молоке: коров-дочерей:
коров-матерей:
Средняя разность:
Проверим гипотезу о существенности средней разности содержания жира в молоке коров-дочерей и коров-матерей. Дисперсия средней разности:
Отсюда средняя ошибка средней разности:
Фактическое значение нормированного отклонения:
Табличное нормированное отклонение при уровне значимости 0,01 и Фактическое значение нормированного отклонения tфакт = 2,42 меньше табличного tтабл = 3,2498, следовательно, гипотеза о существенности средней разности содержания жира в молоке коров-дочерей и коров-матерей не подтверждается. Различия носят случайный характер. Можно с вероятностью 0,99 утверждать, что содержание жира в молоке коров-дочерей зависит от содержания жира в молоке коров-матерей. Это подтверждает и предельная ошибка средней разности, которая равна:
Фактическая средняя разность Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 5.5.
Р и с. 5.5
2. Рассчитайте фактическое и табличное значения нормированного отклонения. 2.1. Выполните команду Сервис, Анализ данных, щелкнув поочередно левой кнопкой мыши. 2.2. В диалоговом окне Анализ данных с помощью левой кнопки мыши установите: Инструменты анализа ® <Парный двухвыборочный t-тест для средних > (рис. 5.6).
Р и с. 5.6
2.3. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.4. На вкладке Парный двухвыборочный t-тест для средних установите параметры в соответствии с рис. 5.7.
Р и с. 5.7
2.5. Щелкните левой кнопкой мыши на кнопке <ОК>. Результаты решения выводятся на экран дисплея в следующем виде (рис. 5.8).
Р и с. 5.8
Пояснения к названию отдельных показателей на рис. 5.8 приведены в табл. 5.2.
3. Критерий c 2 как критерий согласия
Критерий c 2 как критерий согласия используют при проверке принадлежности эмпирического распределения к теоретическому, например, к нормальному, биноминальному, распределению Пуассона и т. п. В этом случае значение критерия c 2 определяют, исходя из частот (f) эмпирического распределения и частот (fo) теоретического распределения:
При этом возможны случаи, когда теоретические частоты заранее известны и когда неизвестны. Во втором случае теоретические частоты определяют на основе теоретического распределения исходя из численности выборки. При проверке гипотезы о соответствии эмпирического распределения теоретическому сравнивают фактическое значение критерия Рассмотрим методику применения критерия c 2 как критерия согласия. Пример 1. В результате учета яйценоскости 50 кур-несушек, содержащихся на птицеферме, был построен интервальный вариационный ряд (табл. 5.4). Средняя арифметическая ряда равна 228,8, а выборочное среднее квадратическое отклонение – 7,95. Т а б л и ц а 5.4 Распределение поголовья
Требуется установить соответствие данного распределения нормальному с уровнем вероятности 0,95. Проверка гипотезы о соответствии теоретическому распределению предполагает расчет теоретических частот этого распределения. Для нормального распределения порядок расчета этих частот следующий: 1) по эмпирическим данным рассчитывают среднюю арифметическую ряда
2) находят нормированное отклонение t каждого эмпирического значения от средней арифметической:
3) по формуле или с помощью таблиц интеграла вероятностей Лапласа находят значение плотности нормального распределения φ (t):
где s – выборочное среднее квадратическое отклонение; π = 3,141593 – постоянное число (отношение длины окружности к ее диаметру); e = 2,718282 – основание натурального логарифма; 4) вычисляют теоретические частоты f0 по формуле:
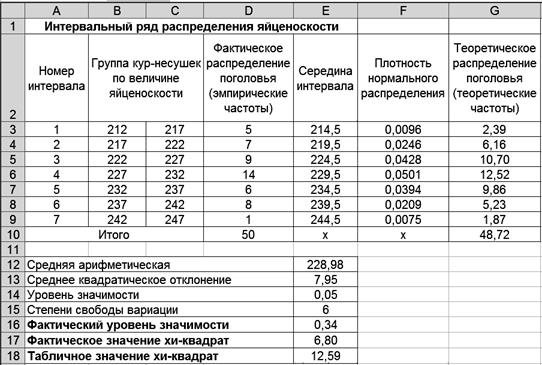
где n − число вариант (сумма частот); h – величина интервала. Фактическое значение критерия Поскольку фактическое значение критерия меньше табличного, то нулевая гипотеза о соответствии эмпирического распределения теоретическому принимается. Распределение яйценоскости кур-несушек соответствует нормальному распределению. Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 5.9.
Р и с. 5.9
2. Рассчитайте плотность нормального распределения поголовья. 2.1. Выделите ячейку F3. 2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <НОРМРАСП> (рис. 5.10).
Р и с. 5.10
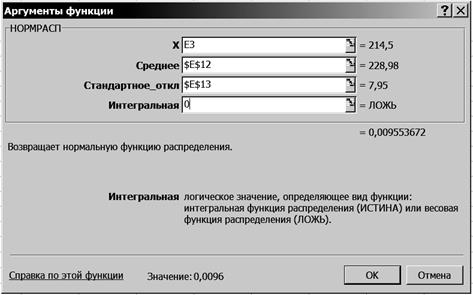
2.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.5. На вкладке НОРМРАСП установите параметры в соответствии с рис. 5.11.
Р и с. 5.11
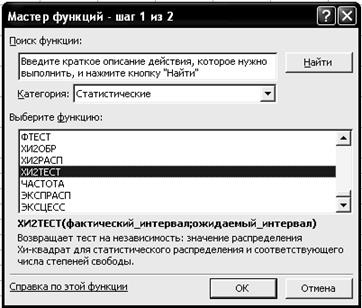
2.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 2.7. Скопируйте ячейку F3 в ячейки F4:F9. 3. Рассчитайте теоретическое распределение поголовья. 3.1. Введите в ячейку G3 формулу =$D$10*(C3-B3)*F3. 3.2. Скопируйте ячейку G3 в ячейки G4:G9. 3.3. Выделите ячейку G10. 3.4. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > 3.5. Выделите ячейки G3:G9. 3.6. Нажмите клавишу <Enter>. 4. Рассчитайте степени свободы вариации. Введите в ячейку Е15 формулу =(2-1)*(A9-1). 5. Рассчитайте фактический уровень значимости. 5.1. Выделите ячейку Е16. 5.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 5.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ТЕСТ> (рис. 5.12).
Р и с. 5.12
5.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 5.5. На вкладке ХИ2ТЕСТ установите параметры в соответствии с рис. 5.13.
Р и с. 5.13
5.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 6. Рассчитайте фактическое значение критерия 6.1. Выделите ячейку Е17. 6.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 6.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ОБР> (рис. 5.14).
Р и с. 5.14
6.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 6.5. На вкладке ХИ2ОБР установите параметры в соответствии с рис. 5.15.
Р и с. 5.15 6.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 7. Определите табличное значение критерия Результаты решения выводятся на экран дисплея в следующем виде (рис. 5.16).
Р и с. 5.16
8. Постройте полигон фактического и теоретического распределения поголовья по яйценоскости. 8.1. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Мастер диаграмм > 8.2. В диалоговом окне Мастер диаграмм (шаг 1 из 4) с помощью левой кнопки мыши установите: Стандартные ® <График> (рис. 5.16).
Р и с. 5.16
8.3. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.4. В диалоговом окне Мастер диаграмм (шаг 2 из 4) установите параметры в соответствии с рис. 5.17.
Р и с. 5.17
8.5. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.6. В диалоговом окне Мастер диаграмм (шаг 3 из 4) введите названия диаграммы и ос Y (рис. 5.18).
Р и с. 5.18
8.7. Щелкните левой кнопкой мыши на кнопке <Далее>. 8.8. В диалоговом окне Мастер диаграмм (шаг 4 из 4) установите параметры в соответствии с рис. 5.19.
Р и с. 5.19
8.9. Щелкните левой кнопкой мыши на кнопке <Готово>. Результаты выводятся на экран дисплея в следующем виде (рис. 5.20).
Р и с. 5.20
9. Вставьте на графике подписи данных. 9.1. Щелкните правой кнопкой мыши на диаграмме и на появившейся вкладке нажмите кнопку <Исходные данные>. 9.2. В диалоговом окне Исходные данные измените подписи оси Х. Для этого выделите ячейки Е64:Е70 (рис. 5.21).
Р и с. 5.21
9.3. Нажмите клавишу <Enter>. Результаты выводятся на экран дисплея в следующем виде (рис. 5.22).
Р и с. 5.22
Пример 2. При скрещивании черных комолых быков с красными рогатыми коровами во втором поколении было получено 97 черных комолых, 25 черных рогатых, 26 красных комолых и 12 красных рогатых потомков. Необходимо установить соответствие данного расщепления расщеплению по закону Менделя 9: 3: 3: 1 с уровнем вероятности 0,99. Теоретическое расщепление определим в соответствии с соотношением 9: 3: 3: 1 и общим поголовьем потомков в выборочной совокупности (табл. 5.5).
Т а б л и ц а 5.5 Распределение поголовья
Фактическое значение критерия Поскольку фактическое значение критерия меньше табличного, то нулевая гипотеза о соответствии эмпирического распределения теоретическому принимается. Расщепление соответствует закону Менделя. Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 5.23.
Р и с. 5.23
2. Рассчитайте общее поголовье и их теоретическое распределение. 2.1. Выделите ячейку В7. 2.2. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > 2.3. Выделите ячейки В3:В6. 2.4. Нажмите клавишу <Enter>. 2.5. Скопируйте ячейку В7 в ячейки С7:D7. 2.6. Введите в ячейку D3 формулу =$B$7*C3/$C$7. 2.7. Скопируйте ячейку D3 в ячейки D4:D6. 3. Рассчитайте степени свободы вариации. Введите в ячейку D11 формулу =(2-1)*(4-1). 4. Рассчитайте фактический уровень значимости. 4.1. Выделите ячейку D12. 4.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 4.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ТЕСТ> (рис. 5.24).
Р и с. 5.24
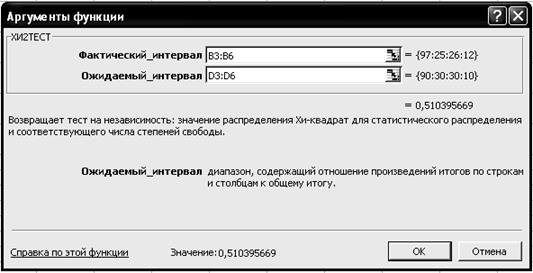
4.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 4.5. На вкладке ХИ2ТЕСТ установите параметры в соответствии с рис. 5.25.
Р и с. 5.25
4.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 5. Рассчитайте фактическое значение критерия 5.1. Выделите ячейку D13. 5.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 5.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ОБР> (рис. 5.26).
Р и с. 5.26
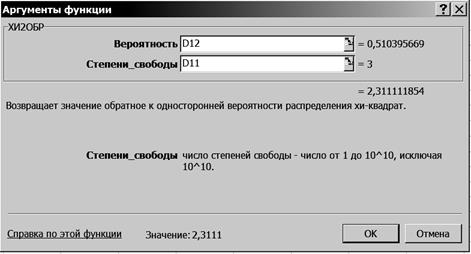
5.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 5.5. На вкладке ХИ2ОБР установите параметры в соответствии с рис. 5.27.
Р и с. 5.27 5.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 6. Определите табличное значение критерия Результаты решения выводятся на экран дисплея в следующем виде (рис. 5.28).
Р и с. 5.28 4. Критерий c 2 как критерий независимости
Критерий c 2 как критерий независимости используют в тех случаях, когда теоретическое распределение неизвестно, и требуется проверить гипотезу о независимости двух выборок, представленных распределением численностей. Например, при сравнении данных полевого опыта. В этом случае теоретические численности по группам определяют на основе общего процента распределения численности по подгруппам, который распространяется на группы:
где
n − число вариант (сумма частот); i − номер группы; k − число групп; j − номер подгруппы; l − число подгрупп. Критерий Рассмотрим методику применения критерия c 2 как критерия независимости. Пример. В стаде, состоящем из 170 коров, был высокий процент абортов. Для проверки препаратов против абортирования поставлен опыт на 50 коровах, остальные 120 коров были контрольными. Распределение численности коров представлено в табл. 5.6. Т а б л и ц а 5.6 Практическое занятие 5 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ 1. Оценка достоверности разности средних. 1 2. Оценка достоверности средней разности. 5 3. Критерий c 2 как критерий согласия. 9 4. Критерий c 2 как критерий независимости. 24 5. Критерий c 2 как критерий однородности. 30
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.19.206 (0.012 с.) |

 ,
, - фактическое нормированное отклонение;
- фактическое нормированное отклонение; - средняя ошибка разности двух выборочных средних.
- средняя ошибка разности двух выборочных средних. и
и  . Общее число степеней свободы вариации равно их сумме
. Общее число степеней свободы вариации равно их сумме 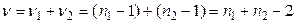 .
. .
.

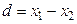
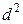
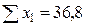


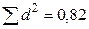
 %;
%; %.
%. %.
%.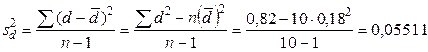 .
. %.
%. .
. степенях свободы вариации в соответствии с данными таблицы значений t -критерия Стьюдента составляет 3,2498.
степенях свободы вариации в соответствии с данными таблицы значений t -критерия Стьюдента составляет 3,2498. %.
%. меньше предельной ошибки
меньше предельной ошибки  , то есть находится внутри границ случайных колебаний.
, то есть находится внутри границ случайных колебаний.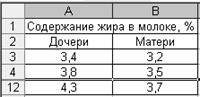



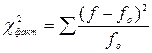 .
.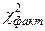 с табличным
с табличным  . Если
. Если 


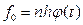

 и среднее квадратическое отклонение s;
и среднее квадратическое отклонение s;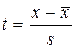 ;
; ,
,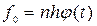 ,
, и
и  степенях свободы вариации равно 12,592 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).
степенях свободы вариации равно 12,592 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).
 или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
 .
.



 .
.








 и
и 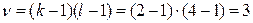 степенях свободы вариации равно 11,344 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).
степенях свободы вариации равно 11,344 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).



 ,
, − теоретические частоты;
− теоретические частоты; − фактические частоты;
− фактические частоты;


