Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретическое распределение коровСодержание книги
Поиск на нашем сайте
Исходя из фактического и теоретического распределений коров фактическое значение
Табличное значение критерия Поскольку Технология решения задачи втабличном процессоре Microsoft Excel следующая. 1. Введите исходные данные в соответствии с рис. 5.29.
Р и с. 5.29
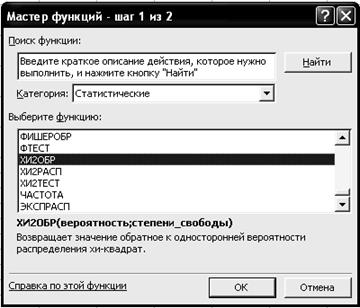
2. Рассчитайте общее поголовье коров, получавших препараты и входящих в контрольную группу. 2.1. Выделите ячейку D4. 2.2. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > 2.3. Выделите ячейки В4:С4. 2.4. Нажмите клавишу <Enter>. 2.5. Скопируйте ячейку D4 в ячейку D5. 3. Рассчитайте общее поголовье и поголовье абортированных коров, используя математическую функцию СУММ. Для этого вставьте в ячейки С7 и С8 функции =СУММ(B4:C5) и =СУММ(B4:B5). Порядок вставки изложен в пункте 2. 4. Рассчитайте процент абортированных коров. Для этого введите в ячейку С9 формулу =C8/C7*100. 5. Рассчитайте теоретическое распределение коров. 5.1. Введите в ячейку В14 формулу =D4*$C$9/100. 5.2. Скопируйте ячейку В14 в ячейку В15. 5.3. Введите в ячейку С14 формулу =D4-B14. 5.4. Скопируйте ячейку С14 в ячейку С15. 6. Рассчитайте степени свободы вариации. Введите в ячейку С18 формулу =(2-1)*(2-1). 7. Рассчитайте фактический уровень значимости. 7.1. Выделите ячейку С19. 7.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 7.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ТЕСТ> (рис. 5.30).
Р и с. 5.30
7.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 7.5. На вкладке ХИ2ТЕСТ установите параметры в соответствии с рис. 5.31.
Р и с. 5.31
7.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 8. Рассчитайте фактическое значение критерия 8.1. Выделите ячейку С20. 8.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> 8.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ХИ2ОБР> (рис. 5.32).
Р и с. 5.32
8.4. Щелкните левой кнопкой мыши на кнопке <ОК>. 8.5. На вкладке ХИ2ОБР установите параметры в соответствии с рис. 5.33.
Р и с. 5.33
8.6. Щелкните левой кнопкой мыши на кнопке <ОК>. 9. Определите табличное значение критерия Результаты решения выводятся на экран дисплея в следующем виде (рис. 5.34).
Р и с. 5.34 5. Критерий c 2 как критерий однородности
Критерий c 2 как критерий однородности применяют в случаях, когда теоретическое распределение неизвестно, и требуется проверить гипотезу об однородности двух или нескольких независимых выборок по некоторому признаку, то есть выяснить относятся ли эти выборки к одной генеральной совокупности. При данной нулевой гипотезе выборочные распределения рассматривают как оценки одной и той же генеральной совокупности. В этом случае за теоретическое распределение численностей по группам берут их среднее фактическое распределение по группам (выборкам). Расчеты ведут также как и при расчете критерия c 2 как критерия независимости. Если фактическое значение критерия Рассмотрим методику применения критерия c 2 как критерия однородности. Пример. Известны данные о распределении численности помесных овец в трех группах в зависимости от настрига шерсти (табл. 5.8). Т а б л и ц а 5.8
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.50.71 (0.007 с.) |

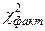 равно:
равно: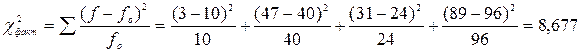 .
. при уровне значимости 0,01 и
при уровне значимости 0,01 и  степени свободы вариации равно 6,635 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»).
степени свободы вариации равно 6,635 (таблица «Значение χ 2 при уровне значимости 0,10, 0,05 и 0,01»). , то гипотеза о независимости распределения рассматриваемых признаков отвергается. Препараты оказывают влияние на абортированность коров. Можно с вероятностью 0,99 утверждать, что применение препаратов позволяет существенно снизить долю коров с абортами.
, то гипотеза о независимости распределения рассматриваемых признаков отвергается. Препараты оказывают влияние на абортированность коров. Можно с вероятностью 0,99 утверждать, что применение препаратов позволяет существенно снизить долю коров с абортами.
 .
. или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.