
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальное число линий в сотСодержание книги
Поиск на нашем сайте
1. Пусть задается уровень обслуживания
2. Пусть
3. 4. Оптимальный размер максимального числа товаров в магазине при отсутствии задалживания спроса. Допущения: 1) Поток покупателей является простейшим с параметром 2) В одни руки отпускается только одна единица товаров 3) Как только происходит продажа единицы товара, сразу подается заявка на замену ее другой единицей 4) Время выполнения заявки 5) Если товар в магазине отсутствует, то покупатель получает отказ и уходит. Пусть а – доход от продажи единицы товара за вычетом издержек выполнения заказа по доставке товара в магазин. Пусть b – издержки хранения единицы товара в течение промежутка времени Средняя прибыль Линия – ячейка. Линия занята – ячейка пуста, Что есть состояние СМО? Обслуживание – выполнение заявки.
Формулы Эрланга для бесконечного пучка и практические приложения Пучок бесконечен Входящий поток – простейший с параметром Время обслуживания распределено показательно с параметром
Состояния СМО можно понимать как качество вызовов на обслуживании
Формулы Эрланга для бесконечного пучка.
Вероятности:
Для систем с отказом формулы Эрланга остаются верными и для
Приложения: 1. Доставка телеграмм. СМО – телеграф, пучок линий – совокупность почтальонов. Допущения: 1) Пусть каждый почтальон одновременно доставляет только одну телеграмму. 2) Считаем, что телеграмма доставляется немедленно по ее получении телеграфом
Какова вероятность того, что в пути находится одновременно 2. Ремонт автомашин. СМО – совокупность ремонтных мастерских. Вызов – автомашина, требующая ремонта. Обслуживание – ремонт. Пусть ремонт начинается немедленно по выходу машины из строя. Поток поломок – простейший с параметром
Пусть а) Среднее число автомашин, находящееся в ремонте, равно б) Вероятность того, что все машины исправны, равна
Упорядоченный пучок линий Пример: упаковочный цех с
Входящий поток – простейший с параметром Время обслуживания – показательно распределено с параметром Рассмотрим частичный пучок длины
Пусть
Обслуживание на Найти
Пусть
Пусть
а)
б)
Обслуживается (среднее число обслуженных вызовов за единицу времени).
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.25.249 (0.01 с.) |

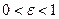 - максимальное значение доли вызовов, которые могут получать отказ в данной СМО. Пусть
- максимальное значение доли вызовов, которые могут получать отказ в данной СМО. Пусть  , это значит, что не больше 10% вызовов могут получать отказ.
, это значит, что не больше 10% вызовов могут получать отказ.
 - средняя плата за обслуживание;
- средняя плата за обслуживание;  - штраф за отказ в обслуживании;
- штраф за отказ в обслуживании;  - оплата труда линии за единицу времени ее работы. Средняя прибыль
- оплата труда линии за единицу времени ее работы. Средняя прибыль  . Определить число линий в данной системе, при котором
. Определить число линий в данной системе, при котором 


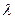 (человек в неделю).
(человек в неделю).  ,
, 
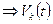 - вероятность того, что спрос будет предъявлен за
- вероятность того, что спрос будет предъявлен за 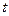 единиц времени на
единиц времени на  единиц товара.
единиц товара. [количество товара в магазине] + [количество заявок]
[количество товара в магазине] + [количество заявок]  .
.  можно понимать либо как максимальный размер товара, либо как максимальное количество заявок.
можно понимать либо как максимальный размер товара, либо как максимальное количество заявок. - непрерывная случайная величина, распределенная по показательному закону с параметром
- непрерывная случайная величина, распределенная по показательному закону с параметром  .
. .
.
 заявка
заявка  . Линия свободна – ячейка заполнена
. Линия свободна – ячейка заполнена 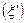 . Всего n линий.
. Всего n линий.
 – на момент
– на момент 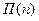 - средняя прибыль за
- средняя прибыль за  (
( ;
; 
 (b учитывает
(b учитывает  (
( , где
, где 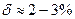 ).
).



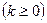
 0, 1, 2, …
0, 1, 2, …  ,
,  ,
,  , …
, … 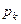 , …
, … - показатель эффективности.
- показатель эффективности.  для конечного пучка.
для конечного пучка. 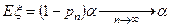 , так как
, так как  .
.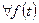 распределения
распределения 
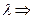 за
за  авт./сут.;
авт./сут.;  сут.
сут. 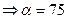 .
. .
. .
.
 (пучок конечный).
(пучок конечный).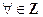 (если пучок бесконечен).
(если пучок бесконечен).

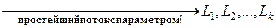
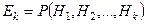 – вероятность отказа на пучке длины
– вероятность отказа на пучке длины  .
.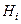 – событие, состоящее в том, что на
– событие, состоящее в том, что на  -ой линии не осуществилось обслуживание.
-ой линии не осуществилось обслуживание.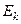 – средняя доля времени, когда в системе
– средняя доля времени, когда в системе 
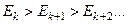
 –вероятность того, что вызов будет обслужен на какой-либо из первых
–вероятность того, что вызов будет обслужен на какой-либо из первых 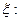 1, 2, …,
1, 2, …,  -?
-?

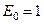
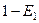


 - интенсивность стационарного потока, пущенного на
- интенсивность стационарного потока, пущенного на  - интенсивность входящего потока.
- интенсивность входящего потока.

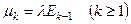


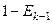
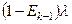

 ,
,  ).
). - вероятность отказа на линии
- вероятность отказа на линии  при условии того, что вызов поступил на эту линию.
при условии того, что вызов поступил на эту линию.
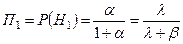
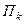 через
через  и
и  .
.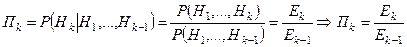
 через
через 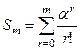





 ;
;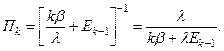
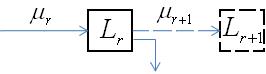


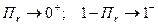
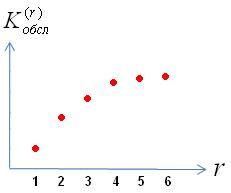

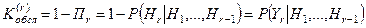 - вероятность того, что вызов будем обслужен на
- вероятность того, что вызов будем обслужен на  -ой линии при условии того, что вызов поступил на
-ой линии при условии того, что вызов поступил на 


