Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о случайном процессе и его марковостиСодержание книги
Поиск на нашем сайте
] ] В ТМО
Возьмем
Понятие о процессах гибели и размножения (ПГР). Стационарное решение и его интерпретация. ОПР:
за а) б) в) Если для случайного процесса выполняются эти условия, он называется ПГР.
Вероятность перехода
В биологии: состояние
Если
Постановка задачи Эрланга для ПГР
Нахождение семейства функций Семейства
Если ]
Нахождение Свойства
Замечание: если
] правое слагаемое меньше
Интерпретация
]
Теорема (эргодическая):
Задание потока вызовов Способ 1: Поток вызовов как случайный процесс. Если Свойства
Необходимо знать функцию распределения вектора
Способ 2:
Свойства
]
Свойства 1. 2.
ОПР: Поток вызовов – последовательность моментов их поступления.
Поток задан, если известна
Простейший поток вызовов
Графики
Академик Хинчин: простейшим является любой поток, который складывается из достаточно большого числа независимых источников вызовов. Простейший поток есть ПГР:
Примеры простейших потоков:
ОПР:
Для простейшего потока Расчёт Пусть существует 100 промежутков единичной длины.
Рассмотрим второе определение:
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.101.251 (0.006 с.) |

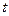 - вещественное число:
- вещественное число:  .
.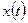 - случайная величина при
- случайная величина при  фиксированном
фиксированном  ,
,  ; известен закон распределения вектора
; известен закон распределения вектора 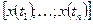 .
. ,…
,… 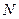 ;
; 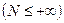
 .
.  .
.  ;
;  - целые, неотрицательные,
- целые, неотрицательные, 
 ;
;  ;
; 
 ;
;  ;
;  ;
;  ;
;  за
за 
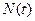 - марковский (без последействия), если
- марковский (без последействия), если 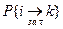 не зависит от состояний, в которых был процесс до
не зависит от состояний, в которых был процесс до  .
. 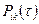 ;
; 
 : 0, 1, 2,…
: 0, 1, 2,…  ,…
,…  - произвольный момент времени;
- произвольный момент времени; 
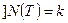 ;
; 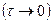
 с вероятностью
с вероятностью 

 с вероятностью
с вероятностью 

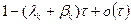
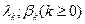 - параметры процесса, не зависящие от прошлых состояний системы.
- параметры процесса, не зависящие от прошлых состояний системы.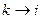 за
за  , если
, если 
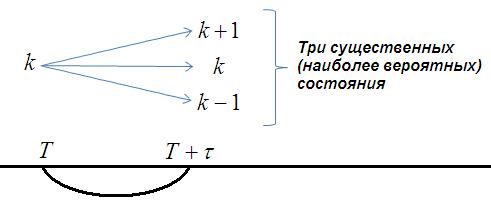
 для
для 
 - это процесс размножения (ПР).
- это процесс размножения (ПР). , то
, то 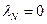 . Если
. Если 
 (для случая
(для случая  ) – это процесс гибели (ПГ).
) – это процесс гибели (ПГ).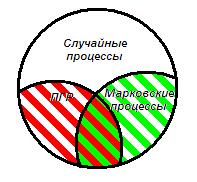
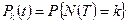

 .
.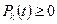 (
( ;
; 

 - взрыв невозможен.
- взрыв невозможен. ,
, 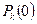
 зависит от
зависит от 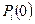
 .
. :
: ,
,  не зависят от
не зависят от 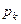 - задача Эрланга в предельной форме – задача нахождения стационарного решения.
- задача Эрланга в предельной форме – задача нахождения стационарного решения.
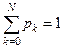




 ,
, 

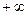 , если
, если 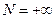
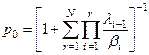 .
.  . Тогда
. Тогда 


 - время пребывания СМО в состоянии
- время пребывания СМО в состоянии  - среднее относительное время пребывания СМО в состоянии
- среднее относительное время пребывания СМО в состоянии  , то есть
, то есть 
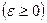
 - средняя длина промежутка времени, в течение которого в системе было ровно
- средняя длина промежутка времени, в течение которого в системе было ровно  .
.  - число вызовов, поступивших в промежутке
- число вызовов, поступивших в промежутке 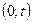 .
. 



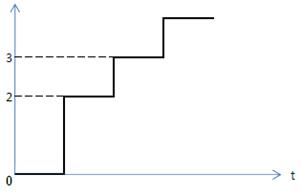
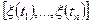 ;
;  ;
;  ;
; 
 , где
, где  - произвольный набор целых неотрицательных чисел.
- произвольный набор целых неотрицательных чисел. ;
; 

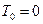 - начальный момент потока.
- начальный момент потока. - момент поступления
- момент поступления 

 . Возможно групповое поступление вызовов.
. Возможно групповое поступление вызовов. ;
; 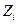 - длина промежутка времени между
- длина промежутка времени между 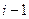 и
и 


 , образуется с помощью случайной величины
, образуется с помощью случайной величины 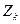
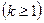 .
.



 ;
; 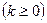 (1)
(1)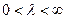 ,
, 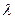 - параметр простейшего потока.
- параметр простейшего потока.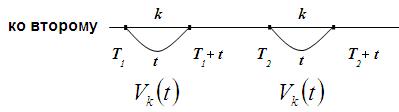
 ,
, 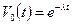

 ,
, 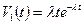
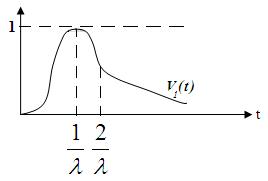
 ,
, 

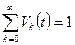


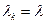 ,
,  :
:
 , где
, где 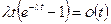
 с вероятностью 0.
с вероятностью 0.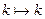 с вероятностью
с вероятностью  , где
, где 
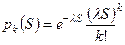 аргумент - площадь.
аргумент - площадь. аргумент - объем.
аргумент - объем. – интенсивность данного стационарного потока – среднее число вызовов, поступающих за промежуток единичной длины
– интенсивность данного стационарного потока – среднее число вызовов, поступающих за промежуток единичной длины  . Среднее число вызовов в промежутке пропорционально длине этого промежутка, причем
. Среднее число вызовов в промежутке пропорционально длине этого промежутка, причем 
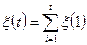 ;
; 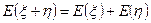 ;
; 
 .
. 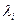 - фактическое число вызовов.
- фактическое число вызовов.
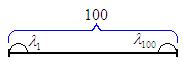
 поток вызовов называется простейшим, если для него выполняется следующее:
поток вызовов называется простейшим, если для него выполняется следующее: распределены по одному и тому же закону, P
распределены по одному и тому же закону, P 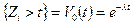 для
для  .
.

 Определения эквивалентны.
Определения эквивалентны.
 Замечание:
Замечание: