
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка опытных данных и составление отчетаСодержание книги
Поиск на нашем сайте
Порядок расчета опытного коэффициента массопередачи 1. Определяется объем аммиака, прореагировавшего с кислотой для условий входа и выхода газа (
где 2. Находится объемная доля аммиака в газе на входе и выходе из абсорбционной трубки
где
3. По уравнению (1) производится перерасчет объемных долей 4. Из материального баланса находится количество абсорбированного водой аммиака 5. Рассчитывается средняя движущая сила абсорбции а) по закону Дальтона вычисляется парциальное давление аммиака в газе на входе и выходе из абсорбционной трубки б) по уравнению (12) определяется конечная концентрация аммиака в жидкости; в) по закону Генри находится равновесная упругость аммиака над раствором г) рассчитывается движущая сила на входе и выходе из абсорбционной трубки и средняя движущая сила процесса. 6. Определяется поверхность контакта фаз. 7. Вычисляется опытный коэффициент массопередачи. Порядок расчета теоретического коэффициента массопередачи 1. По уравнению расхода рассчитывается скорость газа в абсорбционной трубке:
2. Определяется критерий Рейнольдса; кинематическая вязкость аммиачно-воздушной смеси принимается равной 1,4 ×10 –5 м2/с. 3. Вычисляется диффузионный критерий Прандтля; коэффициент молекулярной диффузии аммиака в воздухе принимается равным 0,198 × 10 –4 м2/с. 4. По критериальному уравнению (19) рассчитывается диффузионный критерий Нуссельта. 5. По критерию Нуссельта определяется коэффициент массоотдачи в газовой фазе, который при абсорбции аммиака водой равен теоретическому коэффициенту массопередачи (при этом коэффициент молекулярной диффузии пересчитывается в м2/ч). Расчетные данные заносятся в табл.3. Таблица 2 Значения коэффициента Генри при абсорбции аммиака водой для концентрации раствора менее 10 г/л
Таблица 3 Результаты расчета коэффициентов массопередачи
Окончание табл. 3
Отчет включает схему абсорбционной установки, расчеты определяемых величин, таблицы с опытными и расчетными данными, анализ полученных результатов. КОНТРОЛЬНЫЕ ВОПРОСЫ к лабораторной работе № 1 1. Порядок выполнения работы. 2. Физическая и химическая абсорбция. Требования, предъявляемые к абсорбентам. 3. Способы выражения состава фаз. 4. Равновесие в процессе абсорбции, влияние температуры и давления на равновесие, правило фаз. 5. Константа фазового равновесия, законы Генри и Дальтона. Равновесная линия на диаграмме У–Х. 6. Материальный баланс процесса абсорбции; уравнение рабочей линии и изображение процесса на диаграмм У–Х. 7. Основное уравнение массопередачи для различных фаз, физический смысл и размерность коэффициента К. 8. Определение коэффициента массопередачи по коэффициентам массоотдачи, их влияние на коэффициент К. 9. Средняя движущая сила процесса. 10. Методы расчета абсорберов. 11. Конструкции абсорберов. 12. Конструкции тарелок. Виды и характеристики насадок.
Лабораторная работа №2
Цели лабораторной работы: - знакомство с устройством и работой тарельчатой колонны; - определение числа теоретических тарелок; - расчет опытного и теоретического коэффициента полезного действия тарелок.
Сведения из теории В химической, нефтеперерабатывающей, пищевой и других отраслях промышленности для разделения жидких гомогенных смесей на технически чистые продукты широко применяют ректификацию. Этот процесс основан на различной летучести составляющих смесь компонентов, т.е. на различии в температурах кипения компонентов при одинаковом давлении. Процесс ректификации осуществляют в противоточных аппаратах, называемых ректификационными колоннами. Наибольшее распространение в промышленности получили тарельчатые колонны с колпачковыми, ситчатыми, клапанными и другими типами тарелок. Несколько реже используются насадочные колонны с насадками различного типа. Через ректификационную колонну противотоком – навстречу друг другу – проходят неравновесные по составу потоки пара и жидкости. Поток пара движется в колонне снизу вверх, а жидкость стекает сверху вниз. На каждой тарелке колонны пар и жидкость вступают в контакт. Вследствие отсутствия равновесия между жидкостью и паром на тарелке возникает процесс массообмена (обмен компонентами), в результате которого составы пара и жидкости изменяются, приближаясь к равновесным. Пар становится богаче наиболее летучим или низкокипящим компонентом (НКК), а жидкость – менее летучим или высококипящим компонентом (ВКК). Таким образом, при ректификации одновременно протекают два противоположных процесса: переход НКК из жидкой фазы в паровую и переход ВКК из паровой фазы в жидкую. В этом состоит принципиальное отличие процесса массообмена при ректификации по сравнению с другими массообменными процессами. В конечном итоге пар, выходящий из верхней части колонны, представляет собой практически чистый НКК, который конденсируют в специальных конденсаторах – дефлегматорах. Часть конденсата возвращается обратно на орошение колонны и называется флегмой, а другая часть – дистиллят- отводится как готовый продукт или полупродукт для других производств. Отношение количества флегмы к количеству дистиллята носит название флегмового числа и является одним из важнейших технологических параметров работы ректификационных установок. Из нижней части колонны отводится сравнительно чистый ВКК, который также может служить конечным продуктом ректификации. Восходящий поток пара в колонне образуется за счет кипячения жидкости в обогреваемом кубе-испарителе. Таким образом, в ректификационной колонне осуществляется непрерывный процесс разделения подаваемой в колонну исходной смеси на дистиллят и кубовый остаток. Концентрации получаемых продуктов разделения зависят от многих факторов, в том числе от числа тарелок, эффективности их работы, от величины флегмового числа и др. В промышленности используют ректификационные установки непрерывного и периодического действия. В первом случае разделяемую жидкость непрерывно подают в среднюю часть колонны на так называемую «питающую» тарелку. В установках периодического действия весь объем разделяемой жидкости сразу загружается в куб перед пуском колонны в работу. Наиболее наглядно процесс ректификации можно проследить на схеме тарельчатой колонны (рисунок 1).
Рис. 2-1. Схема массообмена на тарелке На нижнюю тарелку поступает из куба пар состава (кмоль НКК / кмоль смеси), а сверху стекает смесь разделяемой смеси и флегмы. На тарелке 1 жидкость содержит х1 (кмоль НКК / кмоль смеси) низкокипящего компонента. При соприкосновении этой жидкости с восходящим потоком пара состава уо происходит массообмен. В результате из паровой фазы в жидкую поглощается преимущественно высококипящий компонент, а из жидкой фазы в паровую переходит преимущественно НКК. Содержание НКК в паре составит у1, а в предельно возможном случае будет соответствовать равновесному составу у1*, причем у1* > у1 > х5. Этот пар проходит через отверстия вышележащей тарелки 2 и контактирует с находящейся там жидкостью состава х2. На тарелке 2 аналогичным образом происходит массообмен с преимущественным поглощением из паровой фазы в жидкую ВКК и выделением из жидкой фазы в паровую НКК. В результате паровая фаза дополнительно обогатится НКК и будет иметь состав у2, а в предельно возможном случае будет соответствовать равновесному составу у2*, причем у2* > у2 > х2. Жидкая фаза, последовательно перетекая с вышележащей тарелки на нижележащую, постепенно обедняется НКК. При многократном повторении процессов испарения и конденсации, т.е. при соответствующем числе тарелок можно получить вверху колонны практически чистый НКК, а внизу колонны – остаток жидкости в виде высококипящего компонента. Теоретически каждая тарелка колонны представляет собой ступень изменения концентрации. Состав пара при выходе с такой тарелки соответствует равновесному составу жидкости при входе ее на ту же тарелку. Следовательно, теоретически число тарелок равно числу ступеней изменения концентрации для каждого случая ректификации. Тарелка, на которой жидкость полностью перемешена и достигается состояние равновесия массообменных процессов, носит название теоретической тарелки. Коэффициент полезного действия теоретической тарелки принимается равным 100 %. Практически пар на тарелке не успевает достичь равновесного состояния, поэтому число требуемых реальных тарелок всегда будет больше теоретического числа ступеней изменения концентраций. В основе теории процесса ректификации лежат результаты исследований соотношения между составами жидкости и пара при равновесных состояниях. Эти соотношения наиболее просты и понятны в случае так называемых идеальных растворов, компоненты которых растворяются друг в друге без каких-либо химических взаимодействий. Идеальные растворы подчиняются закону межфазного равновесия Рауля: ра* = Ра× х, (1) рв* = Рв(1 – х), (2) где ра* - парциальное давление низкокипящего компонента А в парогазовой смеси над жидкостью в условиях равновесия; Ра - давление насыщенного пара чистого компонента А, являющееся однозначной функцией температуры; рв* - парциальное давление высококипящего компонента В в парогазовой смеси над жидкой смесью в условиях равновесия; Рв – давление насыщенного пара чистого компонента В, являющееся однозначной функцией температуры; х – мольная доля низкокипящего компонента А в жидкости, кмоль А / кмоль смеси. Общее давление паров (П) над жидкостью равно сумме парциальных давлений компонентов: П = ра* + рв* = Рв + (Ра – Рв) х. (3) Согласно уравнениям Клайперона и Дальтона парциальное давление компонента ра*= П×уа, тогда у а = ра* / П, (4) где уа – мольная доля компонента А в парогазовой смеси. Подставляя значение ра* из уравнения (1), получаем:
Для анализа процессов ректификации удобно пользоваться диаграммой Значение х может быть определено из уравнения (3):
Зная мольную массу НКК в жидкости (х), по диаграмме, представленной на рис. 2 можно легко определить соответствующее ему равновесное значение у * (мольную долю НКК в паре) и наоборот.
Рис. 2-2. Равновесная диаграмма у – х для бинарной смеси
На тарелке, согласно правилу Трутона, из жидкости испаряется столько же молей НКК, сколько сконденсируется молей ВКК (вследствие примерного равенства мольных теплот испарения НКК и ВКК). Следовательно, общие молярные потоки пара и жидкости по высоте колонны остаются постоянными. Это постоянство молярных потоков позволяет установить простую зависимость между составами пара и жидкости в любом произвольно взятом горизонтальном сечении ректификационной колонны. Материальный баланс по НКК для всей части колонны, расположенной выше точки ввода жидкой исходной смеси, запишется: Gv × у = GR × х + GД × хД, (7) где GV - количество паров, поднимающихся в колонне снизу вверх, кмоль/c; GR - количество флегмы, стекающей в колонне сверху вниз, кмоль/c; GД - количество дистиллята, отводимого из верхней части колонны, кмоль /с; у - мольная доля НКК в паре; х - мольная доля НКК в стекающей в колонне флегме; хД - мольная доля НКК в дистилляте. Из выражения (7) следует, что для любого поперечного сечения колонны периодического действия мольная доля НКК в паре может быть определена из следующей зависимости:
Это выражение представляет собой зависимость между действительными (неравновесными) составами контактирующих пара и жидкости в любых межтарельчатых сечениях колонны периодического действия. Поскольку GV и GR для всех сечений постоянны, уравнение (5) является уравнением прямой линии, которую обычно называют рабочей линией. Зная Следовательно, рабочая линия в этом случае изображается биссектрисой координатного угла. Пользуясь кривой равновесия и уравнением рабочей линии, можно шаг за шагом определить равновесные составы жидкости и пара по всей высоте колонны и в результате этого определить минимальное число тарелок, необходимое для той или иной заданной степени разделения исходной жидкости. Очень просто и наглядно решается эта задача графическим методом с помощью диаграммы y – x. Примерный вид такой диаграммы, построенной для колонны периодического действия в случае ее работы «на себя», представлен на рис. 2-3. Кривая 1 является кривой равновесия и строится по уравнению (5) или по опытным данным. Прямая 2 (диагональ диаграммы) представляет собой рабочую линию. Допустим, что на этой диаграмме хw является заданным составом жидкости в кубе, а хД – требуемый состав дистиллята. Проведем сечение С1 – С1 (рисунок 1) под тарелкой 1 и определим в этом сечении состав х 1 жидкости, стекающей в куб. Этот состав можно найти, решая уравнение рабочей линии, или по y – x диаграмме (рис. 2-3).
Рис.2-3. Диаграмма y – x колонны периодического действия
Для этого достаточно провести из конца ординаты у w горизонталь до пересечения в точке а1 с рабочей линией. Абcцисса х 1 этой точки и будет представлять собой состав жидкости на тарелке 1, если допустить, что жидкость на ней полностью перемешена, т.е. состав ее во всех точках данной тарелки один и тот же. Зная состав жидкости на тарелке 1, легко найти равновесный состав пара, выходящего после контакта с этой жидкостью, т.е. в сечении C2 – C2. Очевидно, он изобразится на диаграмме ординатой у 1, соответствующей абсциссе х 1. Состав жидкости в сечении C2 – C2, а следовательно, и состав жидкости на тарелке 2 колонны опять находим по уравнению рабочей линии, т.е. проводим из концов ординаты у 1 новую горизонталь до пересечения с рабочей линией. Абсцисса х 2 точки пересечения а2 и будет представлять состав жидкости на тарелке 2. Для определения необходимого числа тарелок такое построение, очевидно, следует продолжить до тех пор, пока не дойдем до тарелки, состав жидкости с которой будет равен заданному составу дистиллята или несколько больше х Д. В результате этого построения на диаграмме получается ступенчатая линия (лестница), число ступенек этой линии и будет представлять необходимое число тарелок. Таким образом определяется число теоретических тарелок n т, поскольку при его определении предполагалось существование на каждой тарелке равновесия между паром и жидкостью. В действительности же в любой работающей колонне этого равновесия не бывает, так как продолжительность контакта между паром и жидкостью на тарелке очень мала, в то время как процесс обмена компонентами (как всякий диффузионный процесс) протекает с некоторой конечной скоростью. По этой причине действительные составы пара на тарелке оказываются меньше теоретических (равновесных) и, следовательно, действительное число тарелок n д, которое может обеспечить заданную степень разделения жидкой исходной смеси, должно быть больше теоретического. Соотношение между ними
обычно определяется как средний коэффициент полезного действия тарелок колонны. Ряд теоретических соображений и многочисленные данные практических наблюдений показывают, что КПД тарелок колонны зависит от целого ряда факторов, количественно учесть которые не представляется возможным; поэтому величину его приходится определять в каждом отдельном случае опытным путем, что и является задачей настоящей работы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.81.255 (0.009 с.) |

 и
и  ):
): , (20)
, (20) – количество 0,1 н. кислоты, налитой в соответствующий дрексель, мл.
– количество 0,1 н. кислоты, налитой в соответствующий дрексель, мл. и
и  :
: , (21)
, (21)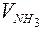 – объем аммиака, прореагировавшего с кислотой для условий входа и выхода газа;
– объем аммиака, прореагировавшего с кислотой для условий входа и выхода газа; – объем вытекшей при этом из аспиратора воды (
– объем вытекшей при этом из аспиратора воды ( и
и  ).
). и
и  ; в этом уравнении
; в этом уравнении  – молекулярная масса аммиака.
– молекулярная масса аммиака. .
. :
: и
и  (общее давление принимается по барометру);
(общее давление принимается по барометру); и
и  (значения констант Генри приведены в табл. 2);
(значения констант Генри приведены в табл. 2); , (22)
, (22)

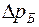










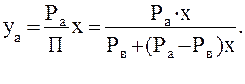 (5)
(5) (6)
(6)
 (8)
(8)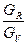 ,
,  и
и  , рабочую линию довольно легко построить. Особенно легко строится она в случае, когда колонна работает «сама на себя», т.е. без выдачи дистиллята. В этом случае
, рабочую линию довольно легко построить. Особенно легко строится она в случае, когда колонна работает «сама на себя», т.е. без выдачи дистиллята. В этом случае  ,
,  и уравнение рабочей линии принимает вид y=x.
и уравнение рабочей линии принимает вид y=x.




