
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретический расчет среднего КПД тарелокСодержание книги
Поиск на нашем сайте
Для сравнения можно рассчитать средний КПД тарелки по критериальному уравнению, полученному путем статистической обработки многочисленных опытных данных для колпачковых и ситчатых тарелок: h = 0,068 × к10,1× к20,115. В этом уравнении безразмерные комплексы
где wn - средняя скорость пара в колонне, м/с; Sсв - относительная площадь свободного сечения тарелки, равная 0,13; hn - высота сливной перегородки, равная 0,02 м; rn, rж – средние плотности пара и жидкости в колонне (таблица 4), кг/м3; Dж - коэффициент молекулярной диффузии легколетучего компонента, м2/ с; s - поверхностное натяжение жидкости в условиях для средней части колонны (таблица 6), н/м. Средняя скорость пара (м/с) определяется по формуле:
где GR - расход флегмы, кг/с; GR = VR × rд; Gд - расход дистиллята при работе колонны; Gд = 0; d - диаметр колонны, м; Mср – средняя молекулярная масса пара, Мср = (Мд + МW) / 2, где Мд и МW - молекулярные массы дистиллята и кубовой жидкости, Мд = 46 × хд + 18(1 – хд), МW = 46 × хW + 18(1 – хW). Средняя плотность пара (кг/м3)
где Тср – средняя температура в колонне, Тср = [(tд + tw)/ 2] + 273. Средняя плотность жидкости (кг/м3) rж = (rд + rw)/ 2, где rд и rw – плотности дистиллята и кубовой жидкости, кг/м3. Коэффициент молекулярной диффузии (м2/с) может быть вычислен по приближенной формуле:
где b - параметр, учитывающий ассоциацию молекул воды и равный 2,6; М - молекулярная масса воды; m - динамический коэффициент вязкости воды при средней температуре в колонне tср, мПа×с (таблица 7) v - мольный объем диффундирующего вещества, для этилового спирта Результаты вычислений сводятся в таблицу 8. Отчет включает в себя схему установки, результаты графического определения числа теоретических тарелок (У – Х диаграмма), расчеты определяемых величин, таблицы 1, 2 и 8. Таблица 4 Зависимость массовой доли этилового спирта (хм)
Таблица 5 Температура кипения и составы жидкости и пара
Таблица 6 Поверхностное натяжение водных растворов этилового спирта s
Таблица 7 Зависимость динамического коэффициента вязкости воды (m) от температуры
Таблица 8 Расчетные результаты
КОНТРОЛЬНЫЕ ВОПРОСЫ к лабораторной работе №2
1. Порядок выполнения работы. 2. Равновесие в процессе ректификации, влияние температуры и давления на равновесие. Равновесные линии различных смесей на диаграмме 3. Закон Рауля и Дальтона, движущая сила процесса. 4. Материальный баланс и уравнения рабочей линии для исчерпывающей и укрепляющей части. 5. Флегма, флегмовое число, коэффициент избытка флегмы. Влияние флегмового числа на число тарелок. 6. Расчет числа тарелок по кинетической кривой. 7. Расчет высоты колонны по числу единиц переноса. 8. Схема ректификационных установок периодического и непрерывного действия. 9. Конструкция тарелок. Виды и характеристики насадок. Лабораторная работа №3
Цели лабораторной работы: – построение кривых сушки и скорости сушки; – определение опытного значения коэффициента массоотдачи и сравнение его с расчетным значением.
Краткие сведения из теории
Сушка – процесс удаления влаги из влажных материалов путем ее испарения и отвода образующихся паров. Весьма распространенным способом проведения этого процесса в промышленных условиях является конвективная сушка, т.е. сушка путем непосредственного соприкосновения сушильного агента (нагретого воздуха, топочных газов) с высушиваемым материалом. Для расчета и проектирования сушильных аппаратов необходимо знать кинетику сушки, которая характеризуется изменением во времени Путем графического дифференцирования кривой сушки может быть определена скорость сушки. Для материала данной влажности скорость сушки выражается тангенсом угла наклона касательной, проведенной к соответствующей точке кривой. Откладывая на графике значения В начале сушки происходит прогрев материала (отрезок АВ) от начальной температуры Далее при сушке наблюдается значительное уменьшение влажности за счет интенсивного поверхностного испарения свободной влаги. При этом в теле возникают градиенты влажности. Под их действием из толщи влажного материала влага перемещается к поверхности раздела фаз за счет массопроводности, испаряется и в виде пара отводится в ядро газовой фазы. Подводимое к материалу тепло полностью затрачивается на испарение влаги, и температура материала остается постоянной, равной температуре «мокрого» термометра. Скорость сушки при этом постоянна и не зависит от влажности материала (отрезок ВС). Влага испаряется из материала на этом этапе сушки так же, как со свободной поверхности жидкости. За счет движущей силы, представляющей собой разность парциальных давлений пара (или разность концентраций) у поверхности материала (насыщенное состояние) и в окружающей среде, влага в виде пара диффундирует через пограничный слой сушильного агента у поверхности материала. Скорость сушки не зависит от сопротивления массопроводности внутри материала и полностью определяется диффузией во внешней среде. Период равномерно падающей скорости (отрезок СD) – период внутренней диффузии влаги. В этом периоде по мере высушивания подвод влаги к внешней поверхности материала становится недостаточно быстрым для компенсации испаряющейся с нее влаги. С этого момента (т. С) на внешней поверхности материала появляются сухие участки, доля увлажненной поверхности уменьшается, зона испарения углубляется внутрь материала, скорость сушки снижается. Скорость испарения влаги со смоченной части поверхности при этом не изменяется.
Рис. 3-1. Кривая скорости сушки
Рис.3-2. Кривая сушки
В этот период скорость процесса сушки лимитируется диффузией влаги из внутренних слоев к поверхности материала, зависит от структуры материала и его температуры, но мало зависит от внешних условий. В течение этого периода скорость сушки пропорциональна содержанию влаги в материале и изменяется по линейному закону. Температура материала при этом повышается ( Период неравномерно падающей скорости (отрезок DЕ) – период внутренней диффузии тепла, влаги и пара. При дальнейшем уменьшении влажности материала вся его поверхность высыхает, влага испаряется преимущественно в глубинных слоях (хотя и имеет место диффузия из глубинных слоев к поверхности). Тепло, необходимое для испарения влаги, передается уже через слой материала, а водяной пар диффундирует в направлении, противоположном тепловому потоку, т.е. через сухой пористый слой к поверхности. На этом участке, вид которого зависит от природы материала и от условий ведения процесса, наблюдается криволинейное падение скорости сушки. При уменьшении влажности материала до равновесной Кинетический закон для периода постоянной скорости сушки выражается уравнениями массоотдачи:
где
Коэффициент массоотдачи
для чисел Рейнольдса в пределах 0…70000 критериальное уравнение имеет вид
Здесь
В этих формулах
Величина
Таблица 1 Зависимость величин
Коэффициент массоотдачи
Кинетический закон для периодов падающей скорости сушки не имеет точного математического выражения ввиду трудности учета большого числа факторов, влияющих на процесс. Поэтому аналитический расчет скорости для этих условий в применении к техническим задачам не проводится.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.221 (0.008 с.) |



 ,
,


 средней влажности материала
средней влажности материала  , [(кг влаги / кг сухого вещества)×100%] и его температуры
, [(кг влаги / кг сухого вещества)×100%] и его температуры  . Зависимость влажности материала от времени сушки
. Зависимость влажности материала от времени сушки  графически изображается кривой линией (рис. 2), которая носит название кривой сушки. Кривую сушки строят по опытным данным путем взвешивания через определенные промежутки времени образца материала с известной начальной влажностью. На рис. 3-2 приведена также кривая нагрева
графически изображается кривой линией (рис. 2), которая носит название кривой сушки. Кривую сушки строят по опытным данным путем взвешивания через определенные промежутки времени образца материала с известной начальной влажностью. На рис. 3-2 приведена также кривая нагрева  высушиваемого материала.
высушиваемого материала. , можно построить кривую скорости сушки
, можно построить кривую скорости сушки  (рис. 3-1). Графическое изображение процесса в виде кривых сушки и скорости сушки дает возможность установить различные периоды его протекания.
(рис. 3-1). Графическое изображение процесса в виде кривых сушки и скорости сушки дает возможность установить различные периоды его протекания. . Влажность материала изменяется при этом незначительно. Скорость сушки возрастает и достигает к концу прогрева максимальной величины. Этот период является кратковременным и характеризует неустановившийся процесс.
. Влажность материала изменяется при этом незначительно. Скорость сушки возрастает и достигает к концу прогрева максимальной величины. Этот период является кратковременным и характеризует неустановившийся процесс.

 и
и 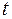 >
>  ).
). скорость испарения влаги падает до 0 (
скорость испарения влаги падает до 0 ( ), температура материала достигает максимального значения – температуры окружающей среды
), температура материала достигает максимального значения – температуры окружающей среды , (1)
, (1) , (2)
, (2) – количество испаренной влаги, кг;
– количество испаренной влаги, кг;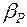 ,
,  – коэффициенты массоотдачи от поверхности материала в окружающую среду, соответственно кг/(м2 × ч × Па) и кг/ (м2× с × кг/кг сухого воздуха);
– коэффициенты массоотдачи от поверхности материала в окружающую среду, соответственно кг/(м2 × ч × Па) и кг/ (м2× с × кг/кг сухого воздуха); – влагосодержание насыщенного воздуха при температуре поверхности материала, кг пара / кг сухого воздуха;
– влагосодержание насыщенного воздуха при температуре поверхности материала, кг пара / кг сухого воздуха; – влагосодержание окружающего воздуха, кг пара / кг сухого воздуха;
– влагосодержание окружающего воздуха, кг пара / кг сухого воздуха; ,
,  – парциальное давление водяного пара соответственно у поверхности материала (в насыщенном состоянии) и в окружающем воздухе, Па;
– парциальное давление водяного пара соответственно у поверхности материала (в насыщенном состоянии) и в окружающем воздухе, Па; – поверхность фазового контакта (поверхность испарения), м2;
– поверхность фазового контакта (поверхность испарения), м2; – время сушки (продолжительность периода постоянной скорости сушки), с.
– время сушки (продолжительность периода постоянной скорости сушки), с. , зависящий от толщины, физических свойств и гидродинамического состояния пограничного слоя газа, находится экспериментально путем обобщения опытных данных критериальными уравнениями вида
, зависящий от толщины, физических свойств и гидродинамического состояния пограничного слоя газа, находится экспериментально путем обобщения опытных данных критериальными уравнениями вида , (3)
, (3) . (4)
. (4) – диффузионный критерий Нуссельта,
– диффузионный критерий Нуссельта, ; (5)
; (5) – критерий Рейнольдса,
– критерий Рейнольдса, ; (6)
; (6) – диффузионный критерий Прандтля,
– диффузионный критерий Прандтля, ; (7)
; (7) – параметрический критерий Гухмана,
– параметрический критерий Гухмана, (8)
(8) – определяющий линейный размер, м;
– определяющий линейный размер, м; – коэффициент диффузии водяных паров в воздухе, м2/c;
– коэффициент диффузии водяных паров в воздухе, м2/c; – скорость воздуха, м/с;
– скорость воздуха, м/с; – плотность воздуха, кг/м3;
– плотность воздуха, кг/м3; – динамическая вязкость воздуха, н×с/м2;
– динамическая вязкость воздуха, н×с/м2; – температура воздуха в сушильной камере, 0С;
– температура воздуха в сушильной камере, 0С; – температура поверхности испарения высушиваемого материала (температура «мокрого» термометра), 0С.
– температура поверхности испарения высушиваемого материала (температура «мокрого» термометра), 0С. и
и  в уравнении (44) зависят от критерия
в уравнении (44) зависят от критерия 
 .
.


