
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы массового обслуживанияСодержание книги Поиск на нашем сайте
Часто приходится сталкиваться с ситуациями возникновения очередей покупателей в кассах магазинов; колонн автомобилей, остановленных светофором; рядов станков, вышедших из строя и ожидающих ремонта, и т. д. Все эти ситуации объединяет то обстоятельство, что системам необходимо пребывать в состоянии ожидания. Ожидание является следствием вероятностного характера возникновения потребностей в обслуживании и разброса показателей обслуживающих систем, которые называют системами массового обслуживания (СМО). Цель изучения СМО состоит в том, чтобы взять под контроль некоторые характеристики системы, установить зависимость между числом обслуживаемых единиц и качеством обслуживания. Качество обслуживания тем выше, чем больше число обслуживающих единиц. Но иметь лишние обслуживающие единицы экономически невыгодно. В промышленности СМО применяются при поступлении сырья, материалов, комплектующих изделий на склад и выдаче их со склада; обработке широкой номенклатуры деталей на одном и том же оборудовании; организации наладки и ремонта оборудования; определении оптимальной численности обслуживающих отделов и служб предприятий и т. д. Основными элементами СМО являются источники заявок, их входящий поток, каналы обслуживания и выходящий поток. В зависимости от характера формирования очереди СМО различают: 1) системы с отказами, в которых при занятости всех каналов обслуживания заявка не встает в очередь и покидает систему необслуженной; 2) системы с неограниченными ожиданиями, в которых заявка встает в очередь, если в момент её поступления все каналы были заняты. Существуют и системы смешанного типа с ожиданием и ограниченной длиной очереди: заявка получает отказ, если приходит в момент, когда все места в очереди заняты. Заявка, попавшая в очередь, обслуживается обязательно. По числу каналов обслуживания СМО делятся на однока-нальные и многоканальные. В зависимости от расположения источника требований системы могут быть разомкнутыми (источник заявок находится вне системы) и замкнутыми (источник находится в самой системе). Рассмотрим в отдельности элементы СМО. Входящий поток: на практике наиболее распространенным является простейший поток заявок, обладающий свойствами стационарности, ординарности и отсутствия последействия. Стационарность характеризуется тем, что вероятность поступления определенного количества требований (заявок) в течение некоторого промежутка времени зависит только от длины этого промежутка. Ординарность потока определяется невозможностью одновременного появления двух или более заявок. Отсутствие последействия характеризуется тем, что поступление заявки не зависит от того, когда и сколько заявок поступило до этого момента. В этом случае вероятность того, что число заявок, поступивших на обслуживание за промежуток времени t,равно k, определяется по закону Пуассона
где l – интенсивность потока заявок, то есть среднее число заявок в единицу времени:
где Для такого потока заявок время между двумя соседними заявками распределено экспоненциально с плотностью вероятности f (t) = le – lt. Случайное время ожидания в очереди начала обслуживания считают распределенным экспоненциально: f (t) = ne – nt, где n – интенсивность движения очереди, то есть среднее число заявок, приходящих на обслуживание в единицу времени:
где Выходящий поток заявок связан с потоком обслуживания в канале, где длительность обслуживания f (tобс) = me – mt, где m – интенсивность потока обслуживания, то есть среднее число заявок, обслуживаемых в единицу времени:
где Важной характеристикой СМО, объединяющей l и m, является интенсивность нагрузки
Рассмотрим n -канальные разомкнутые СМО.
СМО с отказами Заявка, поступившая в систему с отказами и нашедшая все каналы занятыми, получает отказ и покидает систему необслуженной. Показателем качества обслуживания выступает вероятность получения отказа. Предполагается, что все каналы доступны в равной степени всем заявкам, входящий поток является простейшим, длительность (время) обслуживания одной заявки (tобс) распределена по показательному закону. Для расчёта установившегося режима работы СМО с отказами используют следующие зависимости: 1. Вероятность простоя каналов обслуживания, когда нет заявок (k = 0)
2. Вероятность отказа в обслуживании, когда поступившая на обслуживание заявка найдет все каналы занятыми (k = n) Ротк = Рn = 3. Вероятность обслуживания Робс = 1 – Ротк. 4. Среднее число занятых обслуживанием каналов
5. Доля каналов, занятых обслуживанием
6. Абсолютная пропускная способность СМО А = l Робс.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.77 (0.005 с.) |

 ,
,
 ,
,  ,
,  ,
,  ,
,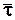 – среднее значение интервала времени между двумя соседними заявками.
– среднее значение интервала времени между двумя соседними заявками. ,
, – среднее значение времени ожидания в очереди.
– среднее значение времени ожидания в очереди. является случайной величиной и часто подчиняется показательному закону распределения с плотностью
является случайной величиной и часто подчиняется показательному закону распределения с плотностью
 ,
, 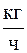 ,
,  ,
, .
.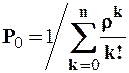 .
. .
. = rРобс.
= rРобс. .
.


