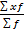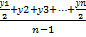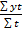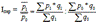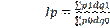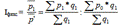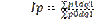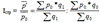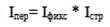Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды рядов динамики, методы расчета среднего уровня в интервальных и моментных рядах динамики.Содержание книги
Поиск на нашем сайте Динамическими рядами в статистической науке называют статистические данные, характеризующие изменения явлений во времени, они строятся для выявления и изучения возникающих закономерностей в развитии явлений в различных сферах жизни общества. В рядах динамики имеются два главных элемента: · показатель времени (t); · уровни развития изучаемого явления (у). В рядах динамики в качестве показателей времени могут выступать определенные даты времени или отдельные периоды. Уровни, образующие ряды динамики, определяют количественную оценку развития во времени исследуемого явления или процесса, они могут выражаться относительными, абсолютными либо средними величинами. Уровни рядов динамики в зависимости от характера исследуемого явления могут относиться к определенным датам времени или к отдельным периодам. Динамический ряд состоит из сопоставимых статистических показателей. Для правильности построения динамических рядов необходимо, чтобы состав исследуемой статистической совокупности относился к одной и той же территории, к одному и тому же кругу объектов и был рассчитан по одной и той же методологии. Данные динамического ряда должны выражаться в одних и тех же единицах измерения, а промежутки времени между значениями ряда должны быть по возможности одинаковыми. Ряды динамики подразделяются на моментные, интервальные и ряды средних величин. Моментные ряды динамики отображают состояние исследуемых процессов на определенные даты времени. Интервальные ряды динамики отображают итоги развития или функционирования исследуемых процессов за отдельные периоды времени. Для характеристики процесса за определенный период рассчитывают средний уровень из всех членов динамического ряда. Способы его расчета зависят от вида динамического ряда. Для интервальных рядов средняя рассчитывается по формуле средней арифметической, причем при равных интервалах применяется средняя арифметическая простая, а при неравных – средняя арифметическая взвешенная. x(cp)= Для нахождения средних значений моментного ряда применяют среднюю хронологическую. Средняя хронологическая моментного ряда равна сумме всех уровней ряда, поделенной на число членов ряда без одного, причем первый и последний члены ряда берутся в половинном размере. у(ср)= Если интервалы между периодами не равны, то применяется средняя арифметическая взвешенная, а в качестве весов берутся отрезки времени между датами(t), к которым относятся парные средние смежных значений уровня. y(ср)= Индексы переменного, постоянного состава и структурных сдвигов. Вычисление и аналитический смысл. Индексный метод широко применяется для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.
Величина этого индекса характеризует изменение средней взвешенной за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя у единиц совокупности.
Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности к общей их численности.
Пример задачи:
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

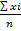 , x(cp)=
, x(cp)=