Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кременчуцький державний політехнічний університетСодержание книги
Поиск на нашем сайте
КРЕМЕНЧУЦЬКИЙ ДЕРЖАВНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ ІНСТИТУТ ЕЛЕКТРОМЕХАНІКИ, ЕЛЕКТРОНІКИ І КОМП’ЮТЕРНИХ ТЕХНОЛОГІЙ
МЕТОДИЧНІ ВКАЗІВКИ ЩОДО ПРАКТИЧНИХ ЗАНЯТЬ ТА КОНТРОЛЬНІ ЗАВДАННЯ З КУРСУ «МЕТОДИ ОПТИМІЗАЦІЇ КЕРУЮЧИХ АЛГОРИТМІВ» ДЛЯ СТУДЕНТІВ ДЕННОЇ ТА ЗАОЧНОЇ ФОРМ НАВЧАННЯ ЗІ СПЕЦІАЛЬНОСТІ 7.091401 «СИСТЕМИ УПРАВЛІННЯ І АВТОМАТИКИ»
КРЕМЕНЧУК 2005
Методичні вказівки щодо практичних занять та контрольні завдання з курсу «Методи оптимізації керуючих алгоритмів» для студентів денної та заочної форм навчання зі спеціальності 7.091401 – “Системи управління і автоматики”
Укладач старш. викладач В.О.Євстіфєєв Рецензент: к.т.н., доц. В.В. Прус
Кафедра САУЕ
Затверджено методичною радою КДПУ
Протокол № _____ від “____” ________2005 р.
Голова методичної ради _________________проф. В.В.Костін ЗМІСТ
ВСТУП
“Методи оптимізації керуючих алгоритмів” – одна з дисциплін навчального плану спеціальності 7.091401 - «Системи управління і автоматики». Необхідність її вивчення випливає з кваліфікаційної характеристики спеціальності, що визначає як мету навчання підготовку інженерів з комп’ютерних систем, здатних самостійно і творчо вирішувати задачі проектування, дослідження, експлуатації систем автоматичного керування і телемеханіки. Методи оптимізації ефективно використовують під час проектування автоматичних пристроїв у технічних і організаційних системах керування. Впровадження оптимальних систем автоматичного керування із застосуванням ЕОМ – це важливий засіб раціонального використання матеріальних, трудових, енергетичних та інших ресурсів. Мета проведення практичних занять під час вивчення курсу «Методи оптимізації керуючих алгоритмів» - закріплення студентами теоретичних знань і набуття навичок, необхідних для правильної постановки задач оптимізації, використання моделей і методів математичного програмування, розв’язування конкретних технічних задач оптимізації. Унаслідок проведення практичних занять студенти повинні навчитися складати і використовувати алгоритми різних способів розв’язування задач оптимізації. Методичні вказівки містять завдання з основних тем курсу, які передбачені навчальним планом, а також приклади розв’язування задач. Варіант завдання студенти визначають за особистим номером у журналі академічної групи. Завдання виконують в окремому зошиті або на аркушах формату А4. Необхідні розрахунки, побудову графіків функцій можна виконувати за допомогою пакетів прикладних програм.
Задача 1 Розв’язування задачі варіаційного числення за методом Ейлера (задача із закріпленими кінцями)
Завдання до задачі Знайти функцію y(t), яка за граничних умов y(t1)=y1 і y(t2)=y2 мінімізує функціонал:
Побудувати графік функції (екстремаль). Граничні умови наведені у таблиці 1.1.
Таблиця 1.1
Приклад 1 Знайти функцію y(t), яка за граничних умов y(1)=2 і y(3)=0 мінімізує функціонал:
Алгоритм методу містить такі етапи: - запис виразу під інтегралом у вигляді функції F(y, y¢); - визначення часткових похідних функції F(y, y¢) за аргументами y і y¢; - складання рівняння Ейлера (1.2); - знаходження розв’язку рівняння Ейлера; - побудова графіка функції y(t). У даному випадку граничні умови: t0=1, tк=3, y(t0) = y0=2; y(tк) = yk=0. Функція F(y,y¢) має вигляд: F(y,y¢) = y2 + k2y¢2, де к=5. Часткові похідні функції F(y,y¢):
Рівняння Ейлера: 2y – 2k2y¢¢ = 0 або y¢¢- y/k2 = 0 (1.8) Розв’язок цього рівняння записуємо у вигляді:
Враховуючи граничні умови, знаходимо С1 і С2:
Тоді С1 = -1,34; С2= 4,43. Розв’язок рівняння Ейлера в остаточному вигляді:
Результати обчислень наведено у таблиці 1.2, графік функції - на рис. 1.2. Таблиця 1.2 Результати обчислень функції y(t)
Відповідно до (1.4) маємо:
Висновок Якщо у задачі оптимізації крім критерію оптимальності (функціоналу І) задані тільки граничні умови y(t0) = y0, y(tк) = yk, обмеження на координати та обмеження на стан системи відсутні, будь-які додаткові умови також відсутні, таку задачу оптимізації розв’язують за допомогою рівняння Ейлера (1.2), або рівняння Ейлера-Пуассона (1.3). Отриманий розв’язок є рівнянням екстремалі, на якій реалізується екстремум заданого функціоналу І.
Контрольні запитання 1. Яку систему керування називають оптимальною? 2. Що таке критерій оптимальності? 3. Що таке функціонал? 4. Що таке задача із закріпленими кінцями? 5. Назвіть класичні методи варіаційного числення. 6. Наведіть рівняння Ейлера і рівняння Ейлера-Пуассона. Поясніть їх суть. 7. Наведіть теорему Лежандра. 8. Які задачі оптимізації розв’язують методом Ейлера? 9. Наведіть алгоритм методу Ейлера. 10. Що таке екстремаль?
Задача 2 Розв’язування задачі варіаційного числення за методом Лагранжа (задача на умовний екстремум)
Завдання до задачі Задача 2.1 Знайти мінімум нелінійної функції f(x1,x2)=(x1-a)2 + (x2-b)2 за обмежень j(x1, x2) = x12 + x22 – R2 = 0. Значення a, b, R наведені у таблиці 2.1. Таблиця 2.1
Навести геометричну інтерпретацію задачі. Приклад 2.1 Знайти мінімум функції f(x1, x2) = 2x12 + x22 за умов: j(x1, x2) = (x1- 2)2 + x2 = 0. Алгоритм методу містить такі етапи: - складання функції Лагранжа: F(x1, x2, l) = f(x1, x2) + lj(x1, x2); - визначення необхідних умов екстремуму функції F(x1, x2, l); - розв’язування системи рівнянь і знаходження координат точок екстремуму функції F(x1, x2, l); - визначення екстремального значення функції f(x1, x2); - наведення геометричної інтерпретації розв’язку задачі. Функція Лагранжа:
Часткові похідні за аргументами функції F:
Необхідні умови екстремуму функції F:
Розв’язуємо цю систему й знаходимо: x1=1; x2= -1; l= 2. Мінімальне значення функції дорівнює: f(x1, x2) = 2x12 + x22 = 3.
Графік функції j(x1, x2) – це парабола. Графіки обох функцій наведено на рис 2.1. Координати точки торкання А (1; -1) визначають мінімум функції f.
Задача 2.2 Визначити оптимальне керування об’єктом, що заданий рівнянням:
у процесі переходу об’єкта з фіксованого початкового стану до кінцевого стану: y(0) = y0; y(¥) = 0, за умови мінімуму функціоналу
Значення Т, k, q, c, y0 наведені у таблиці 2.2. Таблиця 2.2
Приклад 2.2 Визначити оптимальне керування об’єктом, що заданий рівнянням (2.9) у процесі переходу об’єкта з фіксованого початкового стану до кінцевого стану: y(0) = y0; y(¥) = 0, за умови мінімуму функціоналу
Запишемо рівняння об’єкта (об’єкт описується аперіодичною ланкою першого порядку) у вигляді:
де а = -1/Т; b = k/T. Складаємо функцію Лагранжа:
Тобто допоміжний функціонал має вигляд:
З урахуванням того, що
записуємо рівняння Ейлера-Лагранжа (2.4):
З другого рівняння маємо: u=lb/2, тоді можна записати систему двох рівнянь:
З другого рівняння
або
Розв’язок цього рівняння має вигляд:
де Умови стійкості та вимоги y(¥) = 0 задовольняє тільки від’ємний корінь, тому маємо:
З урахуванням граничних умов С1=y(0)=y0. Далі знаходимо:
Тоді: Шукане оптимальне керування:
де
Рівняння (2.18) визначає структуру оптимального регулятора для заданого об’єкта керування і вибраного функціоналу (2.11). Мінімум цього функціоналу гарантує мінімальні відхилення y(t) і u(t) у період перехідного процесу. Вираз (2.19) визначає оптимальне значення коефіцієнта k0.
Висновок Якщо у задачі оптимізації крім критерію оптимальності (функціоналу І), граничних умов y(t0) = y0, y(tк) = yk задані також додаткові обмеження (рівняння об’єкта керування), таку задачу оптимізації можна розв’язати за допомогою методу множників Лагранжа, причому кількість множників Лагранжа дорівнює кількості обмежень.
Контрольні запитання 1. Що таке умовний екстремум? 2. Сформулюйте задачу Лагранжа. 3. Запишіть у загальному випадку функцію Лагранжа. 4. Наведіть рівняння Ейлера-Лагранжа. 5. Чим визначається кількість множників Лагранжа, що входять до функції Лагранжа? 6. Наведіть алгоритм методу множників Лагранжа. Література: [1, с. 88-90], [2, с.32-35], [4, с. 251-261], [6, с.67-70].
Завдання до задачі Задача 3.1 Розв’язати задачу 2.2 методом динамічного програмування. Вихідні дані у таблиці 2.2. Приклад 3.1 Розв’язати задачу (приклад 2.2) методом динамічного програмування. Маємо рівняння об’єкта: Функціонал: Тоді система (3.3) має вигляд:
Звідси знаходимо: dS/dy = - 2u/b;
Отримали квадратне рівняння відносно u, корені якого є шуканими керуваннями:
Другий корінь відкидаємо як такий, що не відповідає умовам стійкості, й остаточно запишемо:
що співпадає з розв’язком (2.19), (2.20). З рівнянь (3.5) можна виключити u і тоді визначити функцію S. Задача 3.2 Розв’язати методом динамічного програмування задачу з обмеженням. Рівняння об’єкта: де x = f(u) – нелінійна функція з обмеженням (рис. 3.1). Функціонал, що мінімізується, має вигляд:
Вихідні дані наведені у таблиці 3.1.
Таблиця 3.1
Приклад 3.2 Розв’язати задачу з обмеженням: де x = f(u) – нелінійна функція з обмеженням (рис. 3.1).
У даному випадку:
Тоді рівняння Беллмана матимуть вигляд:
З другого рівняння отримуємо:
З останнього рівняння: Тоді перше рівняння системи (3.7) матиме вигляд:
Отримали рівняння, аналогічне попередньому прикладу, розв’язок якого має вигляд: Розв’язок рівняння Отже, закон регулювання (з урахуванням від’ємного зворотного зв’язку) має вигляд:
При цьому d = g/k0. Висновок Задачі оптимального керування об’єктами, рівняння яких відомі, простіше розв’язувати методом динамічного програмування Беллмана. Якщо, крім того, накладено додаткові обмеження на координати і керування, такі задачі не можна розв’язати методами класичного варіаційного числення (методами Ейлера, Лагранжа), необхідно застосування сучасних методів, наприклад методу Беллмана.
Контрольні запитання 1. У чому полягає перевага сучасних методів варіаційного числення порівняно з класичними методами? 2. Поясніть суть методу динамічного програмування. 3. Який принцип лежить в основі методу динамічного програмування? 4. Поясніть сутність принципу оптимальності. 5. Наведіть систему рівнянь Беллмана для системи першого порядку з однією керуючою дією.
Література: [3, с. 60-70], [6, с. 72-75].
Завдання до задачі Слідкуюча система заданої структури (рис. 4.1) описується диференціальним рівнянням другого порядку. Для поліпшення якості перехідного процесу виконавчий механізм охоплений жорстким від’ємним зворотним зв’язком за швидкістю. Необхідно визначити оптимальне значення коефіцієнта зворотного зв’язку kз.з., при якому критерій І1 (4.2) набуває мінімального значення. Вихідні дані наведено у таблиці 4.1.
Таблиця 4.1
Передавальна функція замкнутої системи має вигляд:
а диференціальне рівняння буде:
Нехай вхідний сигнал змінюється стрибком від u до 0, тоді, вважаючи у(0)=1;
отримуємо:
Визначимо величину І1 через коефіцієнти диференціального рівняння. Для цього помножимо (4.9) почергово на у і
Врахуємо, що
Тоді після інтегрування системи (4.10) отримаємо:
Звідси
Для знаходження kз.з., що відповідає І1= min, запишемо:
Звідси оптимальне значення kз.з.: Для заданих значень: Т = 0,5 с; k1 = 200; k2 = 0,25 c-1; r1 = 0,01с2, маємо: k0 = k1k2 = 50 c-1; a0 = T/k0 = 0,5/50 = 0,01 c2. Тоді коефіцієнт зворотного зв’язку має значення:
Контрольні запитання 1. Що таке аналітичне конструювання регуляторів? 2. Поясніть суть методу АКР. 3. У якій послідовності виконують аналітичне конструювання регуляторів?
Література: [3, с. 49-60], [6, с. 89-98].
Завдання до задачі Задача 5.1 Об’єкт описується диференціальним рівнянням:
де y(t) - вихідна координата об’єкта; k - коефіцієнт передачі; u(t) - керуючий вплив. Знайти алгоритм керування, що переводить об’єкт з положення y(0)=y0, y¢(0)=0 до рівноважного положення (y=0, y¢=0) за мінімальний час. На керування накладається обмеження: Вихідні дані наведені в таблиці 5.1. Таблиця 5.1
Приклад 5.1 Об’єкт описується диференціальним рівнянням:
де y(t) – вихідна координата об’єкта; u(t) – керуючий вплив; Знайти алгоритм керування, що переводить об’єкт з положення y(0)=-1,5 y¢(0)=0 до рівноважного положення (y=0, y¢=0) за мінімальний час. На керування накладається обмеження: Алгоритм розв’язування задачі містить такі етапи: - визначити передавальну функцію об’єкта управління; - побудувати структурну схему об’єкта; - скласти математичний опис об’єкта у вигляді системи рівнянь, що приведені до нормального вигляду; - визначити складові вектора j=(j1, j2, … jn), ji = yi¢, i=1,2,…n; - визначити складові вектора Y=(Y1,Y2, …Yn); - записати гамільтоніан H=Y×j; - визначити умови максимуму H; - виконати аналіз можливих алгоритмів управління. Уводимо нові змінні: y = y1; dy/dt = y2. Тоді рівняння (5.8) в операційній формі, тобто у зображеннях за Лапласом, має вигляд:
Після перетворень отримуємо передавальну функцію за Лапласом:
Структурну схему об’єкта (рис. 5.2) можна подати у вигляді двох динамічних ланок, що з’єднані послідовно:
Рівняння ланок:
Запишемо рівняння у нормальному вигляді:
Тоді функція Гамільтона буде:
Спряжені рівняння мають вигляд:
Звідси знаходимо: y 1 = с1; y2 = - с1t +c2, (5.15) де с1, с2 – сталі інтегрування.
u = umax×signy2. (5.16) Оскільки функція y2 має один корінь t1=c2/c1, керування u(t) має одну зміну знака (два інтервали керування). Після закінчення керування Оскільки система розімкнута, момент перемикання знаходимо методом стикування розв’язків диференціальних рівнянь. Отже, необхідно знайти моменти часу: t1 – момент зміни знака керування; T = t2 – закінчення керування. У початковий момент часу (t=t0=0) об’єкт знаходиться у точці В (рис. 5.3), тобто S(0) = -S0 = y1(0) = -1,5; Кінцеве значення координат: S(t2) = y1(t2)=0; При цьому з рис. 5.3 видно, що перший інтервал керування є додатним (u = +umax), а другий – від’ємним (u = -umax). Розв’язуємо диференціальне рівняння:
де с1 і с2 – сталі інтегрування. Після диференціювання отримуємо:
Запишемо рівняння (5.16) і (5.17) для різних моментів часу: - для t = t0 = 0 (початок першого інтервалу):
Звідси с10 = 0, с20 = y1(0) = -1,5; - для t = t1 (кінець першого, початок другого інтервалу); оскільки функції
Звідси отримуємо: - для t = t2 = T (кінець другого інтервалу):
Звідси Дорівнюємо вирази для с11 , а також для с21. Тоді отримуємо відповідно:
Після підстановки першого рівняння до другого отримаємо:
Звідси знаходимо: - момент перемикання керування: - момент закінчення руху: Задача 5.2 Визначити закон змінювання струму якоря двигуна постійного струму з незалежним збудженням, що забезпечує відпрацювання кутового переміщення q0 протягом мінімального часу Т при статичному моменті Мс=0 і обмеженні струму якоря |i| £ іmax. Вихідні дані наведено у таблиці 5.2. Таблиця 5.2
Приклад 5.2 Розв’язати задачу 5.2. Рівняння, що описують динаміку двигуна, мають вигляд:
де w - кутова швидкість двигуна; с – струмова стала двигуна; J – момент інерції електропривода. Позначимо: w = y1, q = y2, i = u. Тоді рівняння двигуна матимуть вигляд: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


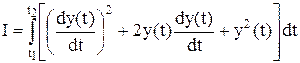 . (1.5)
. (1.5)
 . (1.6)
. (1.6) ,
, 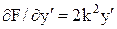 . (1.7)
. (1.7)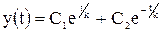 (1.9)
(1.9) (1.10)
(1.10) . (1.11)
. (1.11)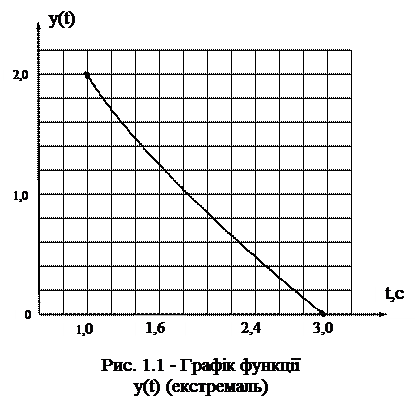
 значить, на кривій (1.11) функціонал (1.6) досягає мінімуму.
значить, на кривій (1.11) функціонал (1.6) досягає мінімуму. Література: [1, с.80-84], [2, с.24-29], [6, с.65-67].
Література: [1, с.80-84], [2, с.24-29], [6, с.65-67].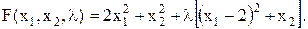 (2.5)
(2.5)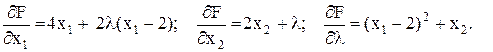 (2.6)
(2.6)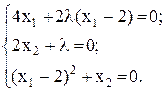 (2.7)
(2.7)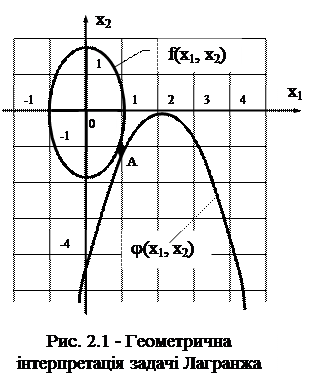 Наведемо геометричну інтерпретацію задачі. Графік функції f(x1, x2) являє собою еліпс з центром у початку координат. Його рівняння після перетворень запишемо у вигляді:
Наведемо геометричну інтерпретацію задачі. Графік функції f(x1, x2) являє собою еліпс з центром у початку координат. Його рівняння після перетворень запишемо у вигляді: (2.8)
(2.8) , (2.9)
, (2.9)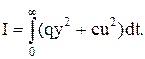 (2.10)
(2.10) (2.11)
(2.11)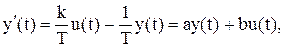
 (2.12)
(2.12)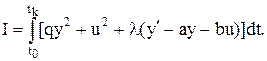 (2.13)
(2.13)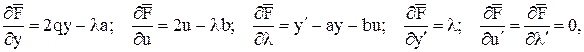
 (2.14)
(2.14)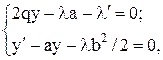 або
або 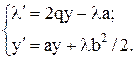 (2.15)
(2.15)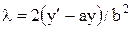 , тоді отримуємо рівняння другого порядку:
, тоді отримуємо рівняння другого порядку:
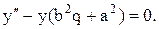 (2.16)
(2.16)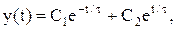
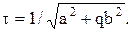
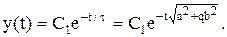 (2.17)
(2.17)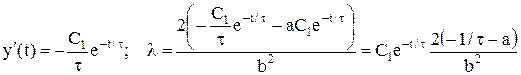 ;
;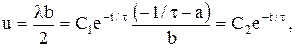 де
де 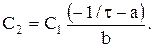
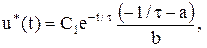 або з урахуванням (2.17):
або з урахуванням (2.17):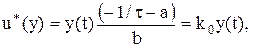 (2.18)
(2.18) (2.19)
(2.19)

 (3.5)
(3.5) або
або 

 (3.6)
(3.6)

 Функціонал, що мінімізується, має вигляд:
Функціонал, що мінімізується, має вигляд: 

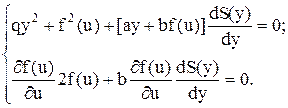 (3.7)
(3.7)




 , де коефіцієнт k0 той самий, що у виразі (3.6).
, де коефіцієнт k0 той самий, що у виразі (3.6). дає константу f(u)=const. З урахуванням обмежень маємо |f(u)| = g.
дає константу f(u)=const. З урахуванням обмежень маємо |f(u)| = g.
 Приклад 4 Розв’язати задачу за умови: r1=0,01с2; k1=200; k2=0,25; Т=0,5 с.
Приклад 4 Розв’язати задачу за умови: r1=0,01с2; k1=200; k2=0,25; Т=0,5 с.
 (4.8)
(4.8) і позначивши:
і позначивши: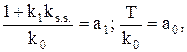
 (4.9)
(4.9) . Тоді отримаємо:
. Тоді отримаємо: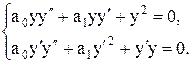 (4.10)
(4.10) і обчислимо такі інтеграли:
і обчислимо такі інтеграли: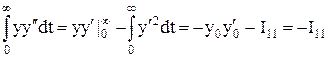 (інтегрування частинами);
(інтегрування частинами);



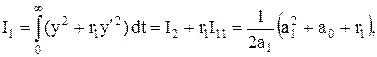 або
або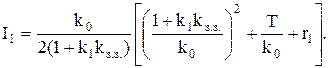


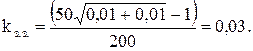
 , (5.7)
, (5.7)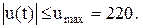
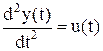 , (5.8)
, (5.8)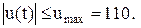
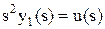 (5.9)
(5.9) . (5.10)
. (5.10)
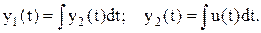 (5.11)
(5.11) (5.12)
(5.12)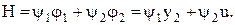 (5.13)
(5.13) (5.14)
(5.14) Функція Гамильтона лінійна відносно u(t), тому для досягнення максимуму необхідно, щоб y2 і u(t) були одного знака, тобто
Функція Гамильтона лінійна відносно u(t), тому для досягнення максимуму необхідно, щоб y2 і u(t) були одного знака, тобто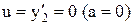 (рис.5.3).
(рис.5.3).
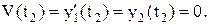
 тобто рівняння зі знакозмінною правою частиною. Характеристичне рівняння: s2 = 0, тобто маємо два нульових кратних кореня s1=s2=0. Тоді розв’язок має вигляд:
тобто рівняння зі знакозмінною правою частиною. Характеристичне рівняння: s2 = 0, тобто маємо два нульових кратних кореня s1=s2=0. Тоді розв’язок має вигляд: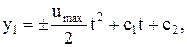 (5.16)
(5.16)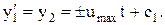 (5.17)
(5.17) (5.18)
(5.18)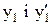 безперервні, то можна виконати стикування розв’язків на межі першого і другого інтервалів:
безперервні, то можна виконати стикування розв’язків на межі першого і другого інтервалів: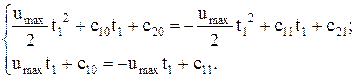 (5.19)
(5.19)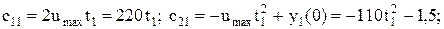
 (5.20)
(5.20)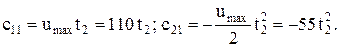
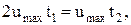 або t2 = T = 2t1;
або t2 = T = 2t1;
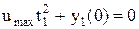 , або
, або