
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Делением целых неотрицательных чисел в количественной теории. ⇐ ПредыдущаяСтр 3 из 3
Т. о., делением во множестве целых неотрицательных чисел называется: 1) отыскание числа элементов в каждом подмножестве, разбиение данного множества на классы по известному числу элементов в заданном множестве и известному числу подмножества (деление на равные части); 2) отыскание числа подмножеств по известному числу элементов в заданном множестве и известному числу элементов в каждом подмножестве (деление по содержанию). Свойства частного. 1. Если частное двух целых неотрицательных чисел существует, то оно находится единственным образом. Доказательство. Допустим противное. Пусть существует 2 частных чисел а и в, т.е а:в=с1, а:в=с2. Тогда по известному числу элементов в данном множестве и числу элементов в каждом подмножестве отыскиваются два числа, являющихся числом подмножеств. Следовательно, разбиение заданного множества проходит на не равномощные подмножества, а это противоречит определению операции деления. Следовательно, если частное существует, то находится единственным образом. Правила деления в количественной теории. Деление на 0 невозможно. Если а это число элементов в данном множестве и множество не разбито на классы, то о числе полученных подмножеств и числе элементов в каждом подмножестве ничего нельзя сказать. Если число а это число элементов в данном множестве и множество разбито на пустые подмножества, но нельзя определить число таких пустых подмножеств, поэтому о делении на 0 сказать не возможно. 1. Деление суммы на число: (а+в):с=а:с+в:с. Доказываем. Из условия равенства Þ, что существует частное чисел а и с, в и с. Пуст а:с=х в:с=у. По определению частного а=с·х в=с·у. Найдем сумму а и в. а+в=с·х+с·у по дистрибутивному свойству с· (х+у). Отсюда по определению частного (а+в):с=х+у (а+в):с=а:с+в:с. 2. Деление разности на число: (а-в):с=а:с-в:с. Докажем по аналогии деления суммы на число, заменив + на -. 3. Деление произведения на число (а·в):с=(а:в)·в Существуют и другие свойства:4. (а:в)·(с:д)=(а·с):(в·д); 5. (а:в):с=а:(в·с);6. а:(в·с)=(а:в):с; 7. а:(в:с)=(а:в)·с
Деление с остатком. 1)Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) — арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число.
Разделить целое число При этом Например, при делении с остатком Можно и 1) или 2)…..одинаково 2)Отыскание пары чисел q и r для заданных чисел а и в, для которых выполняется равенство а=в·q+r называется делением с остатком числа а на число в. Теорема. Для любой пары чисел а и в существует единственная пара чисел q и r, для которых выполняется равенство а=в· q+r 0≤r<в. Доказательство:1) Докажем, что если деление с остатком существует, то r<в. При делении а на в возможны три случая: а) а=в, тогда в·1+0, где q=1, r=0, б) а<в, тогда а=в·0+а, где q=0, r=а, в) а>в, тогда можно найти целый ряд чисел, которые являются произведением в·q, в·1, в·2, в·3, в·4, в·q, в· (q+1). И в данном случае а либо равно одному из перечисленных чисел ряда, тогда выполняется деление на целое число, либо расположено между двумя числами, тогда выполняется деление с остатком. Пусть а расположено между числами: в·q≤а<в· (q+1). Вычтем из обеих частей неравенства в·q. Получим 0≤а-в·q<в. Если обозначить разность (а- в·q) за r, то получим 0≤ r<в. Получили а=в·q+r, r<в,где q - неполное частное, r – остаток от деления числа а на число в. Докажем, что если деление с остатком существует, то пара чисел q и r определяется единственным образом. Допустим противное. Пусть существуют две пары чисел q и r – q1 и r1. а=в·q1+r1 и а =в·q2+r2; в·q1+r1=в·q2+r2 в·q1-в·q2=r2-r1 в(q1-q2)=r2-r1. Так как в левой части равенства есть множитель в, то произведение в(q1-q2) делится на в. Если левая часть равенства делится на в, то и правая должна делится на в, т.е (r2-r1) должна делится на в. Так как r1 <в и r2 <в, то и (r2 –r1)<в. Получили, что меньшее число должно разделиться на большее. Такое деление существует только тогда, когда делимое равно 0. r2 –r1 =0 r2 =r1. Если остатки равны, то подставив их значение в равенство в·q1 +r1 =в·q2 +r2 q1 =q2. Показали, что r и q находятся единственным образом. Ра
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1541; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.187.103 (0.004 с.) |
 на натуральное число
на натуральное число  с остатком означает представить его в виде:
с остатком означает представить его в виде: 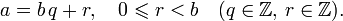
 называется неполным частным, а
называется неполным частным, а  — остатком от деления
— остатком от деления 
 на
на  получаем неполное частное
получаем неполное частное 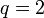 и остаток
и остаток 




