
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие числового выражения. Значение числового выражения. Числовые равенства как высказывания. Свойства истинных числовых равенств.Стр 1 из 3Следующая ⇒
Требования к определению понятий. Классификация понятий. Понятие –это форма абстрактного мышления в которой отражаются существенные признаки предметов. Признаками предметов – называется их свойства,которыми они могут быть похожими и отличаться. Содержимое понятий -это совокупность существенных признаков предметов, которые отражены в этом понятии. Объём - это множество объектов в каждом из которых свойственны все признаки из содержания рассматриваемого понятия. Основные способы определения понятий: 1.через род и вид(указывается род понятия и его видовое отличие(объем-род)). 2.генетический(генезис-это происхождение)-это определение понятия через его происхождение. 3.через абстракцию(натуральным числом- общие свойства класса конечных равномощных множеств) 4.индуктивный-это определение понятий на основе рассуждения от частного к общему. 5.контекстуальный-описательный. 6.аксиматический-аксиомы которым удовлетворяет то или иное понятие(Евклида, Пеано). Определяемое понятие - понятие существенные признаки которого отыскиваются. Определяющее понятие - понятие посредством которого определяется неизвестное понятие. В определении понятия через ближайший род и видовые отличие нужно следить за тем, чтобы использовался ближайший род, но не образовывался порочный круг. Тавтология в определении - логическая ошибка заключающаяся в том, что понятие определяется само через себя. Слишком узкое определение понятия - логическая ошибка, состоящее в том, что нарушается принцип соразмерности, в результате чего объем определяемого понятия оказывается меньше объема определяющего понятия. В определении понятия через ближайший род и видовые отличие нужно следить за тем, чтобы использовалось минимальное и в тоже время достаточное количество существенных признаков видовых отличий. Классификация - распределение предметов какого-либо рода на классы согласно наиболее существенным признакам, присущих предметам данного рода, при этом каждый класс занимает в получившейся системе определенное постоянное место и, в свою очередь, может делится на подклассы. Класс - совокупность (множество) объектов, имеющих один или несколько общих характерных признаков. Род - логическая характеристика класса предметов, в состав которого входят другие классы предметов, являющиеся виддами этого рода. Родовое понятие является подчиняюшщим понятием, в состав которого входят меньшие по объему понятия.
Понятие числового выражения. Значение числового выражения. Числовые равенства как высказывания. Свойства истинных числовых равенств. Числовое выражение –математическое выражение (2+5)-3, А)любое число является числовым выражением, Б)два числа соединены знаками арифметических чисел образуют числовые выражения, В)два и более числа соединены знаками арифметического действия образуют числовые выражения. Значение числового выражения – это число которое получается в результате выполнения всех арифметический действий указанных в числовом выражении. Два числовые выражения соединены знаками равенства образуют числовые равенства (истинные или ложные).Свойства числового равенства: 1)если к обеим истинным числовым равенствам прибавить одно и то же числовое выражение, то в результате получится истинное числовое выражение; 2)если истинное равенство умножить на одно и тоже числовое выражение имеющее значение, то получим истинное числовое выражение; 3)при подчленном сложении 2-ух числовых равенств, то получим истинное числовое равенство.
5. Выражение с переменной. Область определения выражения с переменной. Тождественные преобразования. Тождество. Выражение с переменной: А)всякая буква; Б)буква и числа соединённые знаками арифметического действия и скобками; В)только такие записи являются выражением с переменной которые строятся по пунктам. Значение переменной-числа. Если в выражение с переменной подставить значение переменной и найти значение полученного числового выражения, то получим значение выражения с переменной. Имеет случай когда числовое выражение не имеет значения. Область определения выражения с переменной - называется множество значений переменной при которых с переменной образуется в числовое выражение имеющее значение(не входит значение с переменной когда дробь 0; которые дают отрицательное значение подкоренного значения; выражение стоящее под знаком логарифма должно быть>0√2-х; 2-х≥0
-х≥-2, х≤2 2-1=1-высказывание. Тождество -преобразование выражения с переменной которые не меняют значение этого выражения: формулы сокращения выражения; раскрытие скобок, заключение в скобки(по правилам); действия над алгебраическими дробями с переменной; приведение подобных чисел. Два выражения с переменной полученные одно из другого с помощью тождественных преобразований называют- тождественно равными Тождественным преобразованием выражения называется замена одного выражения другим, тождественно равным ему.
6.Уравнение с одной переменной как предикат вида f(x) = … (x),………Множество корней уравнения. Равносильные уравнения. Теоремы о равносильности уравнений и их следствие. Уравнение с одной переменной как предикат вида f(x) =ψ (x),на Х(1) Множество истинности предиката - решение уравнений; множество корней в зависимости какая переменная входит в значение: линейные уравнения, квадратные, кубические. Каждое значение переменной х входящие в множество истинности предиката 1 называется корнем. Решить уравнение значит найти все его корни., нужно выполнить преобразование над его правой и левой частью- должны быть равносильными(не должны приводить к изменениям его корней). Два уравнения f1(x)=ψ1(x) F2(x)=ψ2(x)- определенны на множестве Х называются равносильными если множество их решений совпадают, другими словами два уравнения называются равносильными если всякий корень 1-го уравнения =корню2-го уравнения и наоборот. Теоремы:1) Если к обеим частям уравнения f(x)=ψ(x),х Следствие: член уравнения можно переносить из одной части в другую поменять знаки переносимого члена на противоположные. Теорема2) Если обе части уравнения 1 умножить на одно и тоже число с переменной g(x)≠0 на множествеХ, получим уравнение f(x).g(x)= ψ(x).g(x) равносильное уравнению 1. Следствие: обе части уравнения можно разделить на любое число ≠0
7.Уравнение с двумя переменными как предикат вида f(x,y)=..(x,y) где х,у Уравнения с двумя переменными называются предикатами f(x,y)=ψ(x,y), которые определенны на множестве Х. Множество истинности предиката является множество решения предиката. Любая пара чисел (а,в) которая принадлежит декартовому 2Х является решением с 2-мя переменными тогда и толькл тогда когда f(a,b)=ψ(a,b)--------линейные 2х+3у=1- бесконечное множество решений. Системой 2-ух уравнений с 1ой переменной называется конъюнкция как предикат: А1Х+В1Х=С1 А2Х+В2У=С2, (А1Х+В1Х=С1)^(А2Х+В2У=С2) - решением будет область истинности конъюнкции предикатов входящих в эту систему. Т1 Методы решения: 1)подстановки(мы из одного уравнения выражаем 1-ну переменную через другую и подставляем то значение в другое. 2)алгебраического сложения – когда уравнения почленно складываются(вычитать, домножать). 3)введение новых переменных. 4)графически. Совокупность уравнений с 2-мя переменными - называется дизъюнкция уравнений как предикатов
А1Х+В1Х=С1 А2Х+В2Х=С2, Т1 (А1Х+В1Х=С1)
8.Неравенство с переменной как предикат вида f(x)<ψ(x),x Неравенства с одной переменной называется предикат одного из следующих видов: 1)строгое- f(x)<ψ(x),x f(x)>ψ(x),x 2)нестрогое- f(x)≤ψ(x),x f(x)≥ψ(x),x Решить неравенство это значит найти множество значений переменной при котором оно обращается в истинное числовое неравенство, х=а решение 1-го неравенства f(x)<..(x), есть истинное число неравенств, другими словами это значит, найти множество истинности предиката, которое задаётся этим неравенством. Множеством истинности этого предиката называется – множеством решений, а каждый элемент с этого множества истинным решением неравенства. Два неравенства f1(x)<ψ1(x), и f2(x)<ψ2(x), x Неравенства f2(x)<ψ2(x), является следствием f1(x)<ψ1(x), если множество решений 2-го неравенства являются подмножеством множества решений 1-го неравенства. Теоремы: Т1)если к обеим частям f(x)<ψ(x),x Т2)если обе части неравенства 1умножить на одно и тоже выражение с переменной g(x), которое принимает положительное значение то получаем неравенство f(x).g(x)< f(x).g(x) равносильно неравенству1. Т3) если обе части неравенства 1умножить на одно и тоже отрицательное число, либо на одно и тоже выражение с переменной определённой на Х и принимает отрицательное значение и при этом знак неравенства полный по противоположности f(x).g(x) >f(x).g(x) равносильно неравенству1. Следствие: 1)члены неравенства переносить из одной части в другую с противоположным знаком 2)члены неравенства можно делить и умножать на одно и тоже положительное число 3)обе части неравенства можно делить –знак переносить противоположный.
10.Теорико- множественный подход к определению натурального числа. Определение натурального числа в НКМ. В основе количественных теорий натурального числа лежит – равномощность. Два множества можно назвать равномощными если можно установить взаимно-однозначное(если множеству В подставить элемент из множества А) соответствие.
Обладает свойствами: рефлективности, симетричности, транзитивности. Классы - это не пустые попарно не пересекающиеся множества объединение которых даёт некоторое множество Х.Отношение равномощности разбивает классы на классы. Класс содержит различное множество объединений общим свойствам(все множества принадлежат классу равномощных) Натуральным числом – называется общие свойство класса конечных равномощных множеств- количество N.
11. Натуральный ряд чисел. Отрезок натурального ряда чисел. Число 0.Множество целых неотрицательных чисел. Отношение <>… Если объединить любое конечное множество с одноилементным множеством, то получим новое множество большой мощности. Если этот бесконечный процесс начать с пустого множества то получим 1,2,3……n - которую называют натуральным рядом чисел. Отрезком натурального ряда чисел называется - множеством всех натуральных чисел 5,6,7,8,9-где не нарушен порядок! 0 –является общим свойством класса пустых множеств. Объединением множеств натуральных чисел с пустыми множествами равно множеству целых неотрицательных чисел(N Целое неотрицательное число а,является n(A1), мы будем называть
Если множество Доказать 2<4 А={а,b } n(A)=2 B={c,d,t,f} n(B)=4 B1={c,d},B1 {c d} B1 ↕ ↕ {a b} A n(B1)=n(A)=2 n(B1)<n(B)
Деление с остатком. 1)Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) — арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число. Разделить целое число При этом Например, при делении с остатком Можно и 1) или 2)…..одинаково 2)Отыскание пары чисел q и r для заданных чисел а и в, для которых выполняется равенство а=в·q+r называется делением с остатком числа а на число в. Теорема. Для любой пары чисел а и в существует единственная пара чисел q и r, для которых выполняется равенство а=в· q+r 0≤r<в. Доказательство:1) Докажем, что если деление с остатком существует, то r<в. При делении а на в возможны три случая: а) а=в, тогда в·1+0, где q=1, r=0, б) а<в, тогда а=в·0+а, где q=0, r=а, в) а>в, тогда можно найти целый ряд чисел, которые являются произведением в·q, в·1, в·2, в·3, в·4, в·q, в· (q+1). И в данном случае а либо равно одному из перечисленных чисел ряда, тогда выполняется деление на целое число, либо расположено между двумя числами, тогда выполняется деление с остатком. Пусть а расположено между числами: в·q≤а<в· (q+1). Вычтем из обеих частей неравенства в·q. Получим 0≤а-в·q<в. Если обозначить разность (а- в·q) за r, то получим 0≤ r<в. Получили а=в·q+r, r<в,где q - неполное частное, r – остаток от деления числа а на число в. Докажем, что если деление с остатком существует, то пара чисел q и r определяется единственным образом. Допустим противное. Пусть существуют две пары чисел q и r – q1 и r1. а=в·q1+r1 и а =в·q2+r2; в·q1+r1=в·q2+r2 в·q1-в·q2=r2-r1 в(q1-q2)=r2-r1. Так как в левой части равенства есть множитель в, то произведение в(q1-q2) делится на в. Если левая часть равенства делится на в, то и правая должна делится на в, т.е (r2-r1) должна делится на в. Так как r1 <в и r2 <в, то и (r2 –r1)<в. Получили, что меньшее число должно разделиться на большее. Такое деление существует только тогда, когда делимое равно 0. r2 –r1 =0 r2 =r1. Если остатки равны, то подставив их значение в равенство в·q1 +r1 =в·q2 +r2 q1 =q2. Показали, что r и q находятся единственным образом.
Ра
Умножение.
Деление: 1102=1*22+1*21+0*20=610 112=1*21+1*20=310 610:310=210
Требования к определению понятий. Классификация понятий. Понятие –это форма абстрактного мышления в которой отражаются существенные признаки предметов. Признаками предметов – называется их свойства,которыми они могут быть похожими и отличаться. Содержимое понятий -это совокупность существенных признаков предметов, которые отражены в этом понятии. Объём - это множество объектов в каждом из которых свойственны все признаки из содержания рассматриваемого понятия. Основные способы определения понятий: 1.через род и вид(указывается род понятия и его видовое отличие(объем-род)). 2.генетический(генезис-это происхождение)-это определение понятия через его происхождение. 3.через абстракцию(натуральным числом- общие свойства класса конечных равномощных множеств) 4.индуктивный-это определение понятий на основе рассуждения от частного к общему. 5.контекстуальный-описательный. 6.аксиматический-аксиомы которым удовлетворяет то или иное понятие(Евклида, Пеано). Определяемое понятие - понятие существенные признаки которого отыскиваются. Определяющее понятие - понятие посредством которого определяется неизвестное понятие. В определении понятия через ближайший род и видовые отличие нужно следить за тем, чтобы использовался ближайший род, но не образовывался порочный круг. Тавтология в определении - логическая ошибка заключающаяся в том, что понятие определяется само через себя. Слишком узкое определение понятия - логическая ошибка, состоящее в том, что нарушается принцип соразмерности, в результате чего объем определяемого понятия оказывается меньше объема определяющего понятия. В определении понятия через ближайший род и видовые отличие нужно следить за тем, чтобы использовалось минимальное и в тоже время достаточное количество существенных признаков видовых отличий. Классификация - распределение предметов какого-либо рода на классы согласно наиболее существенным признакам, присущих предметам данного рода, при этом каждый класс занимает в получившейся системе определенное постоянное место и, в свою очередь, может делится на подклассы. Класс - совокупность (множество) объектов, имеющих один или несколько общих характерных признаков. Род - логическая характеристика класса предметов, в состав которого входят другие классы предметов, являющиеся виддами этого рода. Родовое понятие является подчиняюшщим понятием, в состав которого входят меньшие по объему понятия.
Понятие числового выражения. Значение числового выражения. Числовые равенства как высказывания. Свойства истинных числовых равенств. Числовое выражение –математическое выражение (2+5)-3, А)любое число является числовым выражением, Б)два числа соединены знаками арифметических чисел образуют числовые выражения, В)два и более числа соединены знаками арифметического действия образуют числовые выражения. Значение числового выражения – это число которое получается в результате выполнения всех арифметический действий указанных в числовом выражении. Два числовые выражения соединены знаками равенства образуют числовые равенства (истинные или ложные).Свойства числового равенства: 1)если к обеим истинным числовым равенствам прибавить одно и то же числовое выражение, то в результате получится истинное числовое выражение; 2)если истинное равенство умножить на одно и тоже числовое выражение имеющее значение, то получим истинное числовое выражение; 3)при подчленном сложении 2-ух числовых равенств, то получим истинное числовое равенство.
5. Выражение с переменной. Область определения выражения с переменной. Тождественные преобразования. Тождество. Выражение с переменной: А)всякая буква; Б)буква и числа соединённые знаками арифметического действия и скобками; В)только такие записи являются выражением с переменной которые строятся по пунктам. Значение переменной-числа. Если в выражение с переменной подставить значение переменной и найти значение полученного числового выражения, то получим значение выражения с переменной. Имеет случай когда числовое выражение не имеет значения. Область определения выражения с переменной - называется множество значений переменной при которых с переменной образуется в числовое выражение имеющее значение(не входит значение с переменной когда дробь 0; которые дают отрицательное значение подкоренного значения; выражение стоящее под знаком логарифма должно быть>0√2-х; 2-х≥0 -х≥-2, х≤2 2-1=1-высказывание. Тождество -преобразование выражения с переменной которые не меняют значение этого выражения: формулы сокращения выражения; раскрытие скобок, заключение в скобки(по правилам); действия над алгебраическими дробями с переменной; приведение подобных чисел. Два выражения с переменной полученные одно из другого с помощью тождественных преобразований называют- тождественно равными Тождественным преобразованием выражения называется замена одного выражения другим, тождественно равным ему.
6.Уравнение с одной переменной как предикат вида f(x) = … (x),………Множество корней уравнения. Равносильные уравнения. Теоремы о равносильности уравнений и их следствие. Уравнение с одной переменной как предикат вида f(x) =ψ (x),на Х(1) Множество истинности предиката - решение уравнений; множество корней в зависимости какая переменная входит в значение: линейные уравнения, квадратные, кубические. Каждое значение переменной х входящие в множество истинности предиката 1 называется корнем. Решить уравнение значит найти все его корни., нужно выполнить преобразование над его правой и левой частью- должны быть равносильными(не должны приводить к изменениям его корней). Два уравнения f1(x)=ψ1(x) F2(x)=ψ2(x)- определенны на множестве Х называются равносильными если множество их решений совпадают, другими словами два уравнения называются равносильными если всякий корень 1-го уравнения =корню2-го уравнения и наоборот. Теоремы:1) Если к обеим частям уравнения f(x)=ψ(x),х Следствие: член уравнения можно переносить из одной части в другую поменять знаки переносимого члена на противоположные. Теорема2) Если обе части уравнения 1 умножить на одно и тоже число с переменной g(x)≠0 на множествеХ, получим уравнение f(x).g(x)= ψ(x).g(x) равносильное уравнению 1. Следствие: обе части уравнения можно разделить на любое число ≠0
7.Уравнение с двумя переменными как предикат вида f(x,y)=..(x,y) где х,у Уравнения с двумя переменными называются предикатами f(x,y)=ψ(x,y), которые определенны на множестве Х. Множество истинности предиката является множество решения предиката. Любая пара чисел (а,в) которая принадлежит декартовому 2Х является решением с 2-мя переменными тогда и толькл тогда когда f(a,b)=ψ(a,b)--------линейные 2х+3у=1- бесконечное множество решений. Системой 2-ух уравнений с 1ой переменной называется конъюнкция как предикат: А1Х+В1Х=С1 А2Х+В2У=С2, (А1Х+В1Х=С1)^(А2Х+В2У=С2) - решением будет область истинности конъюнкции предикатов входящих в эту систему. Т1 Методы решения: 1)подстановки(мы из одного уравнения выражаем 1-ну переменную через другую и подставляем то значение в другое. 2)алгебраического сложения – когда уравнения почленно складываются(вычитать, домножать). 3)введение новых переменных. 4)графически. Совокупность уравнений с 2-мя переменными - называется дизъюнкция уравнений как предикатов А1Х+В1Х=С1 А2Х+В2Х=С2, Т1 (А1Х+В1Х=С1)
8.Неравенство с переменной как предикат вида f(x)<ψ(x),x Неравенства с одной переменной называется предикат одного из следующих видов: 1)строгое- f(x)<ψ(x),x f(x)>ψ(x),x 2)нестрогое- f(x)≤ψ(x),x f(x)≥ψ(x),x Решить неравенство это значит найти множество значений переменной при котором оно обращается в истинное числовое неравенство, х=а решение 1-го неравенства f(x)<..(x), есть истинное число неравенств, другими словами это значит, найти множество истинности предиката, которое задаётся этим неравенством. Множеством истинности этого предиката называется – множеством решений, а каждый элемент с этого множества истинным решением неравенства. Два неравенства f1(x)<ψ1(x), и f2(x)<ψ2(x), x Неравенства f2(x)<ψ2(x), является следствием f1(x)<ψ1(x), если множество решений 2-го неравенства являются подмножеством множества решений 1-го неравенства. Теоремы: Т1)если к обеим частям f(x)<ψ(x),x Т2)если обе части неравенства 1умножить на одно и тоже выражение с переменной g(x), которое принимает положительное значение то получаем неравенство f(x).g(x)< f(x).g(x) равносильно неравенству1. Т3) если обе части неравенства 1умножить на одно и тоже отрицательное число, либо на одно и тоже выражение с переменной определённой на Х и принимает отрицательное значение и при этом знак неравенства полный по противоположности f(x).g(x) >f(x).g(x) равносильно неравенству1. Следствие: 1)члены неравенства переносить из одной части в другую с противоположным знаком 2)члены неравенства можно делить и умножать на одно и тоже положительное число 3)обе части неравенства можно делить –знак переносить противоположный.
10.Теорико- множественный подход к определению натурального числа. Определение натурального числа в НКМ. В основе количественных теорий натурального числа лежит – равномощность. Два множества можно назвать равномощными если можно установить взаимно-однозначное(если множеству В подставить элемент из множества А) соответствие. Обладает свойствами: рефлективности, симетричности, транзитивности. Классы - это не пустые попарно не пересекающиеся множества объединение которых даёт некоторое множество Х.Отношение равномощности разбивает классы на классы. Класс содержит различное множество объединений общим свойствам(все множества принадлежат классу равномощных) Натуральным числом – называется общие свойство класса конечных равномощных множеств- количество N.
11. Натуральный ряд чисел. Отрезок натурального ряда чисел. Число 0.Множество целых неотрицательных чисел. Отношение <>… Если объединить любое конечное множество с одноилементным множеством, то получим новое множество большой мощности. Если этот бесконечный процесс начать с пустого множества то получим 1,2,3……n - которую называют натуральным рядом чисел. Отрезком натурального ряда чисел называется - множеством всех натуральных чисел 5,6,7,8,9-где не нарушен порядок! 0 –является общим свойством класса пустых множеств. Объединением множеств натуральных чисел с пустыми множествами равно множеству целых неотрицательных чисел(N Целое неотрицательное число а,является n(A1), мы будем называть
Если множество Доказать 2<4 А={а,b } n(A)=2 B={c,d,t,f} n(B)=4 B1={c,d},B1 {c d} B1 ↕ ↕ {a b} A n(B1)=n(A)=2 n(B1)<n(B)
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 17754; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.47.253 (0.151 с.) |
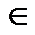 Х прибавить одно и тоже число либо одно и тоже выражение с переменной g(x)то получим уравнение f(x)+g(x)= ψ (x)+g(x) равносильное уравнению1.
Х прибавить одно и тоже число либо одно и тоже выражение с переменной g(x)то получим уравнение f(x)+g(x)= ψ (x)+g(x) равносильное уравнению1. Т2
Т2 Т2
Т2 }=N0)
}=N0) В1
В1 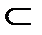 B,B1˜A
B,B1˜A на натуральное число
на натуральное число  с остатком означает представить его в виде:
с остатком означает представить его в виде: 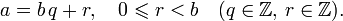
 называется неполным частным, а
называется неполным частным, а  — остатком от деления
— остатком от деления 
 на
на  получаем неполное частное
получаем неполное частное 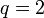 и остаток
и остаток 








