
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные предпочтительные ряды чиселСодержание книги
Поиск на нашем сайте
7.1. Производные предпочтительные ряды чисел устанавливаются для случаев, в которых из-за естественных закономерностей не могут быть применены геометрические ряды, регламентированные разделами 1, 2, 3, 4, 5 и 6 настоящего стандарта. Производные ряды получают путем простейшего преобразования основных и дополнительных рядов предпочтительных чисел, и, соответственно, производные ряды также делятся на основные и дополнительные. 7.2. Убывающие ряды положительных предпочтительных чисел получают на основе убывающей геометрической прогрессии,
Эти ряды чисел применяются для установления значений параметров, асимптотически приближающихся к нулю, например, загрязнения вещества. 7.2.1. Убывающие ряды положительных предпочтительных чисел содержат числа, приведенные в табл.2, 4 и 5. 7.2.2. Обозначение убывающего ряда положительных предпочтительных чисел получают добавлением к обозначению каждого основного или дополнительного ряда предпочтительных чисел знака " 7.2.3. Для убывающих рядов положительных предпочтительных чисел сохраняются положения пп.1.2, 1.3, 4.1 и раздела 5 настоящего стандарта. 7.3. Комплементарные предпочтительные ряды чисел получают на основе убывающей геометрической прогрессии. Выражение для
где
Для образования комплементарных рядов следует брать предпочтительные числа, приведенные в табл.2, 4, 5 и вычитать их из 10 Комплементарные предпочтительные ряды чисел следует использовать для установления значений параметров, асимптотически стремящихся к 10 7.3.1. Члены комплементарного ряда за некоторым исключением не есть предпочтительные числа. 7.3.2. Обозначение комплементарного ряда получают добавлением к обозначению исходного основного или дополнительного ряда предпочтительных чисел знака "-", например, 7.3.3. Для комплементарных предпочтительных рядов чисел сохраняются положения п.4.1. и раздела 5. 7.4. Арифметические предпочтительные ряды чисел получают на основе прогрессии,
при условиях, что где
Арифметический ряд предпочтительных чисел представляет собой арифметическую прогрессию с разностью Примечание. Условие, что 7.4.1. Арифметические предпочтительные ряды чисел должны применяться при установлении значений параметров: сумма или разность которых должна принадлежать тому же ряду (например, при блочном проектировании и модульной координации размеров); лежащих в ограниченных пределах, в которых целесообразна линеаризация (например, интервалы температур окружающего воздуха, определяющие нормы, размеры обуви и одежды); когда равномерная градация обусловлена удобством использования (например, значения аргументов в таблицах, градуирование шкал приборов); когда нужны точные целые значения (например, эталонные значения параметров); выраженных в значениях логарифмов или в децибеллах (например, нормы на уровень шума). 7.4.2. Точные значения членов арифметических рядов в интервале 0-1000 представляют собой мантиссы десятичного логарифма исходных (точных) значений предпочтительных чисел. 7.4.3. Арифметические предпочтительные ряды чисел ограничены в обоих направлениях условиями п.7.4. 7.4.4. Предпочтительные арифметические ряды могут быть положительными и отрицательными или могут переходить через нуль. 7.4.5. При сложении или вычитании числа предпочтительного арифметического ряда дают число того же ряда, если оно не выходит за его пределы. 7.4.6. Обозначения и разности основных и дополнительных арифметических предпочтительных рядов чисел устанавливаются по табл.6. Таблица 6
Примечание. Точные значения членов основных арифметических рядов в интервале от 0 до 1000 приведены в табл.2 в графе "Мантисса десятичного логарифма". 7.4.7. В обозначениях арифметических предпочтительных рядов чисел должны указываться их разность и числа, ограничивающие ряд, например: А 2 (-10...+10)
А 0,5 (0...40)
А 1250 (5·10 7.4.8. Для арифметических предпочтительных рядов чисел сохраняются положения п.4.1 и раздела 4 настоящего стандарта. Примечание. Обозначение выборочных арифметических рядов образуется аналогично обозначениям выборочных рядов предпочтительных чисел по п.4.2.
СПЕЦИАЛЬНЫЕ РЯДЫ ЧИСЕЛ
8.1. В случаях, когда ряды чисел, перечисленные в разделах 1-7 не могут быть применены из-за естественной закономерности изменения значений параметра, используют специальные ряды чисел, правила построения которых приведены в приложении 3.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.252.21 (0.007 с.) |

 -й член которой равен
-й член которой равен .
. ", например:
", например:  5,
5,  ,
, - целое число или нуль.
- целое число или нуль. .
. 5,
5, 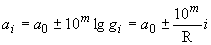
 кратно 10
кратно 10  и
и  ,
,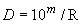 , причем и сама разность, и члены ряда имеют точные значения.
, причем и сама разность, и члены ряда имеют точные значения. можно сформулировать так: при отсутствии ограничений арифметический предпочтительный ряд чисел должен содержать в качестве одного члена нуль.
можно сформулировать так: при отсутствии ограничений арифметический предпочтительный ряд чисел должен содержать в качестве одного члена нуль. 5
5
 ...2·10
...2·10  ).
).


