
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие правила применения предпочтительных чиселСодержание книги
Поиск на нашем сайте
И ПРЕДПОЧТИТЕЛЬНЫХ РЯДОВ ЧИСЕЛ
9.1. Предпочтительные числа и их ряды должны использоваться: при установлении стандартных значений и рядов стандартных значений величин; при нормировании значений исходных параметров продукции, условий ее существования и процессов, а также разрешенных и допускаемых их отклонений; при нормировании значений параметров продукции, связанных логарифмируемой зависимостью с исходными параметрами, значения которых нормируются посредством предпочтительных чисел; при приведении значений параметров предметов и процессов (в т.ч. природных констант), если использование предпочтительных чисел не влечет выхода за пределы допускаемого отклонения. 9.2. Производные и специальные ряды чисел допускается применять только в случае, если применение рядов предпочтительных чисел невозможно или нецелесообразно. 9.3. В случае альтернативных вариантов предпочтение следует отдавать ряду, имеющему меньшее число градаций, а также основному ряду перед выборочным и составным. 9.4. Применение дополнительных рядов предпочтительных чисел и предпочтительных рядов чисел допускается только в том случае, если ряд 9.5. Не допускается образовывать составные ряды путем соединения предпочтительных рядов различных видов, например, геометрического и арифметического, комплементарного и геометрического и т.д.
ПРИЛОЖЕНИЕ 1 Справочное СВОЙСТВА РЯДОВ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
1. Произведение или частное двух предпочтительных чисел, а также положительные или отрицательные степени чисел ряда дают предпочтительное число этого же ряда с относительной ошибкой в пределах от -1,01 до +1,26%. 2. Куб любого числа ряда 3. Члены ряда 4. В рядах, начиная с
5. Ряд 6. Основные и дополнительные ряды предпочтительных чисел содержат все целые степени десяти. ПРИЛОЖЕНИЕ 2 Рекомендуемое Предпочтительные выборочные ряды предпочтительных чисел
Примечание: Использование выборочных рядов, знаменатель которых равен знаменателю основного ряда, допускается только для установления значений зависимых параметров ПРИЛОЖЕНИЕ 3 Справочное СПЕЦИАЛЬНЫЕ РЯДЫ ЧИСЕЛ И ЗНАЧЕНИЙ ВЕЛИЧИНЫ (ПАРАМЕТРА) 1. Двоичный ряд чисел.
Применяется в вычислительной технике. 2. Форматные ряды стандартных значений линейного размера стороны листа Данный ряд линейного размера образуется из условия, что стороны формата листа связаны соотношением Отсюда выражение для
значение площадь исходного листа равна 1 м ряд должен содержать линейный размер 1 м. В первом случае Во втором случае Отсюда форматный ряд линейного размера в мм, будет в первом случае: Во втором случае: 3. Ряды линейных размеров, полученные на основе "золотого сечения". Значения линейных размеров прямоугольника с соотношением сторон на основе "золотого сечения" выбираются из соотношения:
Прямоугольник с таким соотношением сторон может быть составлен из квадратов или прямоугольников с таким же соотношением сторон.
Прямоугольники "золотого сечения" позволяют разместить наибольший объем информации, они обладают максимальной эстетической ценностью и могут быть рекомендованы, например, для книг, картин, плакатов, линейных размеров различного рода экранов, панно, витрин, фасадов строительных сооружений и т.д. Выражение для
Значение площадь исходного прямоугольника равна 1 м
В первом случае
Во втором случае ряд в мм имеет вид:
4. Ряд значений модульного линейного размера Данный ряд линейного размера образуется из условия, что параллелепипед при делении большего размера пополам должен образовать два подобных ему параллелепипеда, линейные размеры которых соответствуют предпочтительным значениям, точно стыкуются друг с другом. Для обеспечения названного требования значения линейных размеров сторон модуля должны быть связаны соотношением:
Отсюда выражения для
Из условия, что исходный объем параллелепипеда равен 1 м
Данный ряд может быть использован при блочно-модульном конструировании. 5. Стандартный упаковочно-модульный ряд линейного размера Стандартный упаковочно-модульный ряд линейного размера представляет собой модификацию предпочтительного модульного ряда линейного размера. Данный ряд для внутренних линейных размеров упаковки вместо соотношения
Использование стандартного упаковочно-модульного ряда линейных размеров обеспечивает следующее: два тела, сложенные малыми сторонами, точно заполняют внутреннее пространство третьего, большего тела при укладке их вдоль меньшего размера этого тела; средний и больший наружный линейные размеры тела образуются путем добавления единичной толщины стенки к внутреннему линейному размеру. Для внутренних линейных размеров ряд стандартных значений имеет вид:
6. Арифметические ряды времени и углового размера В тех случаях, когда для измерения времени используются секунды и минуты или минуты и часы, а для измерения угловых размеров - угловые градусы, минуты и секунды, могут использоваться предпочтительные специальные арифметические ряды, образованные по п.7.4 настоящего стандарта и имеющие разности 3 и 1,5.
7. Стандартные ряды номинальной емкости электрических конденсаторов и номинального сопротивления резисторов Данные ряды представляют собой геометрические ряды чисел со знаменателями, приведенными в таблице.
Тождественны следующие выборочные ряды:
8. Двоично-десятичный ряд чисел Данный ряд представляет собой последовательность чисел ...10
т.е. ряд
Ряд может быть рекомендован для норм, каждая из которых имеет самостоятельное применение, например, масштабов выполнения карт, чертежей, цены деления средств измерений.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 646; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.158.197 (0.01 с.) |

 40 или созданный на его основе производный ряд чисел не обеспечивает требуемого числа градаций. Применение дополнительного ряда должно сопровождаться подробным обоснованием.
40 или созданный на его основе производный ряд чисел не обеспечивает требуемого числа градаций. Применение дополнительного ряда должно сопровождаться подробным обоснованием. , т.е. длины окружности и площади круга примерно равны предпочтительным числам, если диаметр - предпочтительное число.
, т.е. длины окружности и площади круга примерно равны предпочтительным числам, если диаметр - предпочтительное число.
 -й член ряда находится из выражения
-й член ряда находится из выражения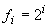
 , т.е. меньший формат получается путем разрезания большего формата при сохранении соотношения сторон.
, т.е. меньший формат получается путем разрезания большего формата при сохранении соотношения сторон.
 выбирается из двух условий:
выбирается из двух условий: ;
; 0,841 м.
0,841 м. 1 м.
1 м.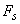 ...1189, 841, 594, 420, 297, 210, 148, 105, 74, 52, 37, 26, 18, 13, 9...
...1189, 841, 594, 420, 297, 210, 148, 105, 74, 52, 37, 26, 18, 13, 9... ...1414, 1000, 707, 500, 353, 250, 170, 125, 88, 62, 44, 31, 22, 15, 11...
...1414, 1000, 707, 500, 353, 250, 170, 125, 88, 62, 44, 31, 22, 15, 11... 1,618 или
1,618 или  0,618.
0,618. .
.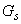 ...2058, 1272, 785, 485, 300, 185, 115, 70, 44, 27, 17, 10...
...2058, 1272, 785, 485, 300, 185, 115, 70, 44, 27, 17, 10... ...2618, 1618, 1000, 618, 382, 236, 146, 90, 56, 34, 21, 13...
...2618, 1618, 1000, 618, 382, 236, 146, 90, 56, 34, 21, 13... ;
;  .
. .
. , определяется следующий ряд значений линейных размеров модуля в мм (
, определяется следующий ряд значений линейных размеров модуля в мм ( :...1260, 1000, 794, 630, 500, 397, 315, 250, 198...
:...1260, 1000, 794, 630, 500, 397, 315, 250, 198... 1,2599 использует соотношение
1,2599 использует соотношение 1,29152
1,29152 : 1000, 775, 600, 494, 359, 279, 215, 187, 129, 100.
: 1000, 775, 600, 494, 359, 279, 215, 187, 129, 100.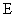 6
6

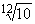



 , 2·10
, 2·10 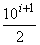 , 10
, 10  ...
... :...1, 2, 5, 10...
:...1, 2, 5, 10...


