
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяция и экстраполяция в динамических рядах.Содержание книги
Поиск на нашем сайте
Исследование динамики соц.эк. явлений создает базу для прогнозирования т.е. для определения ориентированных размеров уровней явления в будущем. Некоторые экстраполяции и интерполяции связаны с определением неизвестных уровней динамического ряда. Экстрополяция – определение будущих размеров уровня. Интерполяция – определение отсутствующего промежуточного уровня ряда. Интерполяцию можно провести при помощи: среднегодового абсолютного прироста ∆y: Yn-Y1/n-1, потом + (-) Y99+∆y. Среднегодового коэф роста Кр, потом умножить. Среднее арифметическое соседних уровней. При экстрополяции можно исходить из того, что тенденции присущие развитию данного явления за известный отрезок времени сохранятся в будущем. Используется ∆y и Кр.
1. Значение индексов и их классификация. 2. Индивидуальные индексы стоимости (товарооборота), цен, физического объема. 3. Построение индексов в агрегатной форме. Индексируемая величина и статистический вес. 4. Средние индексы, тождественные агрегатным. 5. Выбор базы и весов при построении индексов. Системы индексов (цепных и базисных). Билет №22 Значение экономических индексов и их классификация. Индекс – особый статистический относительный показатель, характеризующий соотношение во времени или пространстве различных социально-экономических явлений.
Например: Ip = Iq =
Классификация индексов 1) по степени охвата По степени охвата различают индивидуальные, сводные (общие) и групповые индексы. А) Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления, например изменения объема производства отдельных видов продукции. Б) Сводные индексы рассчитываются для измерения динамики сложного явления, составные части которого непосредственно несоизмеримы, например изменения физического объема продукции, включающей разноименные товары. В) Групповые индексы охватывают не все элементы сложного явления, а только часть их, например физический объем продукции по отдельным отраслям промышленности. Групповые индексы отражают закономерности в развитии отдельных частей изучаемых явлений. 2) по базе сравнения По базе сравнения все индексы делятся на динамические и территориальные. А) Динамические индексы отражают изменение явления во времени. Например, индекс цен на продукцию в 2007г. по сравнению с предыдущим годом. При исчислении динамических индексов происходит сравнение значения показателя в отчетный период со значением этого же показателя за предыдущий (базисный) период. Динамические индексы, как и ряды динамики, бывают базисными и цепными. Базисные динамические индексы – результат сравнения текущих уровней с одним фиксированным уровнем, принятым за базу. Например, Iq = I’’q = Цепные динамические индексы – результат сравнения текущих уровней с непосредственно предшествующими. Например, Ip = I’’p = Б) Территориальные индексы применяются для межрегиональных сравнений. Эти индексы имеют большое значение в международной статистике при сопоставлении показателей социально-экономического развития разных стран. Например, индекс цен на автомобили в США по сравнению с Японией. 3) по виду весов Вес индекса – величина постоянная, одинаковая в числителе и знаменателе, служит для соизмерения индексируемых величин. По виду весов индексы бывают с постоянными и переменными весами. А) Постоянный вес – вес базисного периода. С постоянными весами рассчитываются индексы физического объема продукции (индекс Ласпейреса, где p0 – постоянный вес). Б) Переменный вес – вес текущего периода. С переменными весами рассчитываются индексы цен (индекс Пааше, где q1 – переменный вес). 4) В зависимости от формы построения В зависимости от формы построения различаются индексы агрегатные и средние. А) Агрегатный индекс – сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина – признак, изменение которого изучается), а другая остается неизменной в числителе и знаменателе (вес индекса). Агрегатные индексы – основная форма общих индексов. Пример: Ip = Б) Средние индексы – производные, они получаются в результате преобразования агрегатных индексов, а следовательно, тождественны им. Средний индекс вычисляется как средняя величина из индивидуальных индексов. Средние индексы делятся на арифметические и гармонические. a) Средний арифметический индекс тождествен агрегатному индексу, только если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Например, Iq = b) Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса. Например, Ip = Так как 5) по характеру объекта исследования По характеру объекта исследования общие индексы подразделяются на индексы количественных и качественных показателей. В основе такого деления лежит вид индексируемой величины. К первой группе, например, относятся индексы объема продаж долларов США на ММВБ, а ко второй – индекс курса немецкой марки. 6) по объекту исследования по объекту исследования индексы бывают: производительности труда, себестоимости, физического объема продукции, стоимости продукции и т.д. 7) по составу явления По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава и переменного состава. А) Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Индекс переменного состава отражает изменение не только индексируемой величины, но и структуры совокупности (весов). Например: Iпс = Б) Индекс постоянного состава – индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Индекс фиксируемого состава определяется как агрегатный индекс. Например: Iфс = 8) по периоду исчисления По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные. Билет №23 Индивидуальные индексы стоимости (товарооборота), цен, физического объема. Индивидуальные индексы получают в результате сравнения однотоварных явлений. Например, индекс цен на растительное масло определяется как отношение цены на этот товар в текущем периоде к цене базисного периода. В зависимости от экономического значения индивидуальные индексы бывают физического объема продукции, цен, товарооборота и т.д. 1) Индивидуальный индекс физического объема продукции Индивидуальный индекс физического объема продукции iq рассчитывается по формуле: iq = Этот индекс показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько процентов составляет рост (снижение) выпуска товара. Если из значения индекса, выраженного в процентах, вычесть 100%, то полученная величина покажет, на сколько процентов возрос (уменьшился) выпуск продукции. 2) Индивидуальный индекс цен Индивидуальный индекс цен ip рассчитывается по формуле ip = 3) Индивидуальный индекс стоимости продукции Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на ее цену (p). Индивидуальный индекс стоимости продукции ipq рассчитывается по формуле ipq = Этот индекс отражает, во сколько раз изменилась стоимость какого-либо товара в текущем периоде по сравнению с базисным или сколько процентов составляет рост (снижение) стоимости товара. При этом: ip Пример № 1 Имеются следующие данные об объеме продаж картофеля на муниципальном рынке в одном из городов страны:
Вычислить индивидуальные индексы цены, физического объема и стоимости картофеля. Решение: а) Индивидуальный индекс физ. объема. iq = Мы получили, что физ. объем проданного картофеля в текущем периоде по сравнению с базисным возрос на 25% (125%-100%), или на 5000 кг, и составил 125% от уровня продаж базисного периода. б) Индивидуальный индекс цен. ip = Мы получили, что уровень цен на картофель в текущем периоде по сравнению с базисным возрос на 50% (150%-100%), или на 10 руб. за кг., и составил 150% от уровня цен базисного периода. в) Индивидуальный индекс товарооборота. ipq = Мы получили, что товарооборот картофеля в текущем периоде по сравнению с базисным возрос на 87,5% (187,5%-100%), или на 350000 руб. (750000 – 400000), и составил 187,5% от товарооборота базисного периода. Рост товарооборота картофеля в текущем периоде по сравнению с базисным произошел как за счет роста цен, так и за счет роста физ. объема продаж. Пример № 2 Определить индивидуальные индексы цены, физ. объема и стоимости мясных продуктов, если известно следующее:
Решение: а) Индивидуальный индекс цены. ip = Мы получили, что уровень цен на мясные продукты в текущем периоде по сравнению с базисным уменьшился на 9,1% (90,1%-100%), или на 0,2 долл. за ед., и составил 90,9% от уровня цен базисного периода. б) Индивидуальный индекс товарооборота. ipq = Мы получили, что товарооборот мясных продуктов в текущем периоде по сравнению с базисным возрос на 24% (124%-100%), или на 2400 долл.(12400 – 10000), и составил 124% от товарооборота базисного периода. Очевидно, что рост товарооборота мясных продуктов в текущем периоде по сравнению с базисным произошел из-за роста физ. объема продаж. в) Индивидуальный индекс физ. объема iq = Мы получили, что физ. объем проданных мясных продуктов в текущем периоде по сравнению с базисным вырос на 36,4% (136,4% - 100%), или на 1654 кг (12400/2,0 – 10000/2,2) и составил 136,4% от уровня продаж базисного периода. Билет №24
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.217 (0.009 с.) |

 - агрегатный индекс цен с весами текущего периода (формула Пааше);
- агрегатный индекс цен с весами текущего периода (формула Пааше); - агрегатный индекс физического объема с весами базисного (предыдущего) периода (формула Ласпейреса).
- агрегатный индекс физического объема с весами базисного (предыдущего) периода (формула Ласпейреса). ; I’q =
; I’q =  ;
; - базисные индексы Ласпейреса.
- базисные индексы Ласпейреса.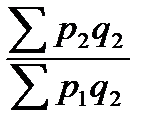 ;
;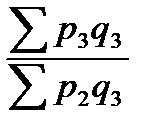 - цепные индексы Пааше.
- цепные индексы Пааше. 
 - средний арифметический индекс физического объема продукции, где весом является стоимость продукции базисного периода, также как и в формуле Iq =
- средний арифметический индекс физического объема продукции, где весом является стоимость продукции базисного периода, также как и в формуле Iq =  q0 = q1, то обе формулы могут быть преобразованы друг в друга.
q0 = q1, то обе формулы могут быть преобразованы друг в друга.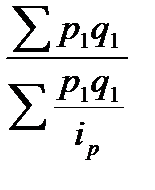 - средний гармонический индекс цен, где весом является стоимость продукции текущего периода, также как и в формуле Ip =
- средний гармонический индекс цен, где весом является стоимость продукции текущего периода, также как и в формуле Ip =  = p0, то обе формулы могут быть преобразованы друг в друга.
= p0, то обе формулы могут быть преобразованы друг в друга. =
=  - индекс переменного состава себестоимости продукции.
- индекс переменного состава себестоимости продукции. =
=  - индекс фиксированного состава себестоимости продукции.
- индекс фиксированного состава себестоимости продукции. , где q1 – физический объем данного товара в текущем периоде, а q0 – физический объем данного товара в базисном периоде.
, где q1 – физический объем данного товара в текущем периоде, а q0 – физический объем данного товара в базисном периоде. , где p1 – цена на данный товар в текущем периоде, а p0 – цена на данный товар в базисном периоде. Таким образом, этот индекс характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным.
, где p1 – цена на данный товар в текущем периоде, а p0 – цена на данный товар в базисном периоде. Таким образом, этот индекс характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным. , где p1q1 – стоимость данного товара в текущем периоде, а p0q0 – стоимость данного товара в базисном периоде.
, где p1q1 – стоимость данного товара в текущем периоде, а p0q0 – стоимость данного товара в базисном периоде. iq = ipq
iq = ipq = 1,25 (или 125%)
= 1,25 (или 125%) = 1,5 (или 150%)
= 1,5 (или 150%) =
=  = 1,875 (или 187,5%)
= 1,875 (или 187,5%) =0,909 (или 90,9%)
=0,909 (или 90,9%) = 1,24 (или 124%)
= 1,24 (или 124%) =
=  =
= 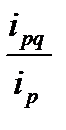 =
=  = 1,364 (или 136,4%)
= 1,364 (или 136,4%)


