Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проектирование аналоговых и цифровых фильтровСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лабораторная работа № 1 Проектирование аналоговых и цифровых фильтров
Цель работы: изучение реализации процесса выборки с запасом и расчета параметров аналоговых и цифровых фильтров. Задание на выполнение работы: Разработать аналоговый и цифровой фильтр для параметров сигнала. Параметры сигнала:
Р, дБ = -57
Расчетная дискритизация = 20500 Гц, но мы её увеличиваем до 25000 по модели построения фильтра
Рисунок 1. Схема для тестирования разработанного фильтра
a=abs(fft(xcov(yout))); f = 25000*(0:10001)/20002; plot(f(1:10001),a(1:10001));
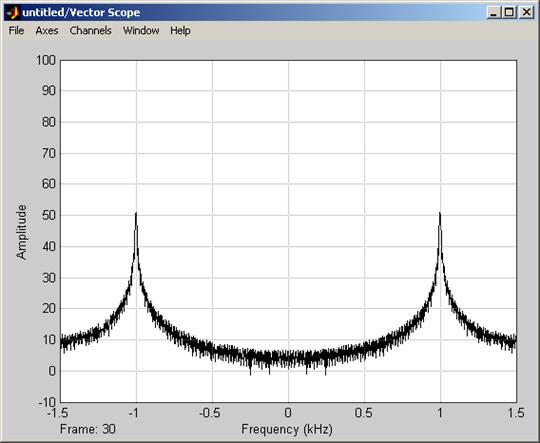
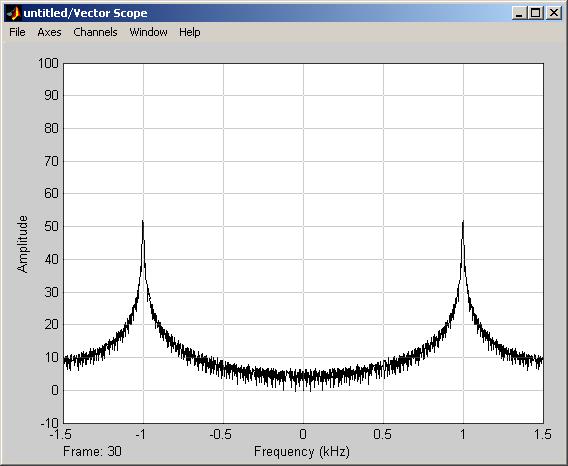
Рисунок 2. Спектр выходного сигнала
Рисунок 3. Одна из секций разработанного фильтра
Вывод:
- Получится фильтр из меньшего числа секций
- Получится фильтр из большего числа секций
Лабораторная работа № 2 Изучение цифровой квадратурной модуляции
Цель работы: использование глазковой диаграммы (eyediagram) и диаграммы рассеяния (scatterplot) для анализа квадратурной модуляции сигнала в системе связи. listing: N = 16; Fd = 1; Fs = N * Fd; Delay = 3; Symb = 60; M = 16; load sig15.yyy; s=sig15(9900:10300); indx=quantiz(s,-2:0.2:1); plot(indx) msg_orig = indx; msg_tx = modmap(msg_orig,Fd,Fd,'qask',M); x = complex(msg_tx(:,1),msg_tx(:,2)); [y, t] = rcosflt(x, Fd, Fs); plot(t, real(y)); h1 = eyediagram(y, N); ss = get(0,'ScreenSize'); fp = get(h1,'position'); set(h1,'position',[ss(3)*.99-fp(3) ss(4)*.9-fp(4) fp(3:4)]);
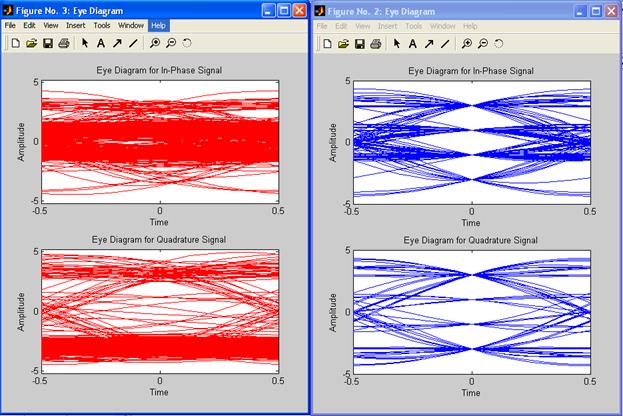
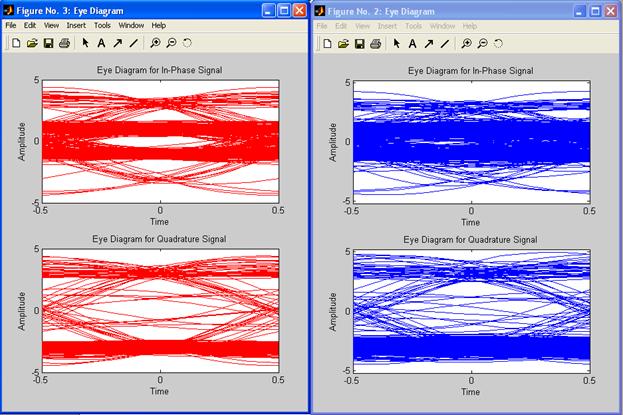
Рис.1 Глазковая диаграмма
yReal = real(y); h2 = eyediagram(yReal, N);
Рис.2 Глазковая диаграмма реальной части сигнала
yy = y(1+Delay*N:end-Delay*(N+2)); h3 = eyediagram(yy, N);
Рис.3 Глазковая диаграмма
NumSym = 2; h4 = eyediagram(yy, N*NumSym, NumSym);
Рис.4 Глазковая диаграмма
h5 = eyediagram(yy, N, 1, N/2);
Рис.5 Глазковая диаграмма “Закрытый глаз”
Функция SCATTERPLOT h6 = scatterplot(yy, N);
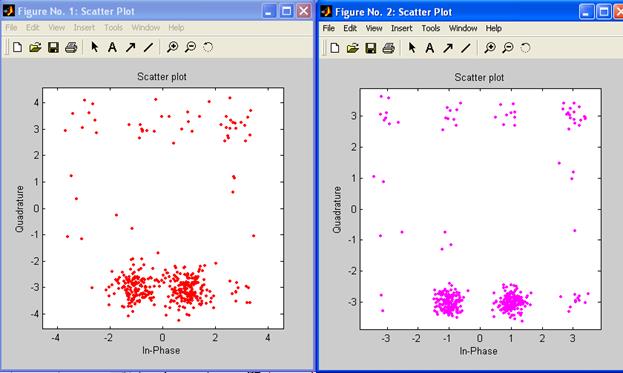
Рис.6 Диаграмма рассеяния h7 = scatterplot(yy, 1, 0, 'c-'); hold on; scatterplot(yy, N, 0, 'b.',h7); hold off;
Рис.7 Диаграмма рассеяния SNR = 15; sig_rx1 = awgn(msg_tx,SNR,'measured',1234,'dB'); sig_rx = complex(sig_rx1(:,1),sig_rx1(:,2)); [fsig_rx, t2] = rcosflt(sig_rx, Fd, Fs); tfsig_rx = fsig_rx(1+Delay*N:end-Delay*(N+1),:); plot(t, real(y),'b-', t2, real(fsig_rx),'r-');
Рис. 8 Сигнал/шум
h(1) = eyediagram(yy, N,1); h(2) = eyediagram(tfsig_rx, N,1,0,'r-');
% перемещение диаграммы к стороне экрана fp = get(h(1),'position'); set(h(1),'position',[ss(3)*.99-fp(3) ss(4)*.9-fp(4) fp(3) fp(4)]); set(h(2),'position',[ss(3)*.86-fp(3) ss(4)*.65-fp(4) fp(3) fp(4)]);
Рис.9 Индекаторная диаграмма h(3) = scatterplot(yy, N, 0, 'b.'); h(4) = scatterplot(tfsig_rx, N, 0, 'r.');
Рис.10 Диаграмма рассеяния SNR = 20; sig_rx1 = awgn(msg_tx,SNR,'measured',4321,'dB'); sig_rx = complex(sig_rx1(:,1),sig_rx1(:,2)); [fsig_rx2, t2] = rcosflt(sig_rx, Fd, Fs); tfsig_rx2 = fsig_rx2(1+Delay*N:end-Delay*(N+1),:); plot(t, real(y),'b-', t2, real(fsig_rx2), 'm-'); pause %%
Рис.11 Сигнал шум 20 ДБ plot(t, real(fsig_rx),'r-',t2,real(fsig_rx2),'m-'); h(1) = eyediagram(tfsig_rx, N,1); h(2) = eyediagram(tfsig_rx2, N,1,0,'r-');
Рис.12 Индекаторная диаграмма 2х сигналов h(3) = scatterplot(tfsig_rx, N, 0, 'r.'); h(4) = scatterplot(tfsig_rx2, N, 0, 'm.');
Рис.13 Диаграмма рассеяния 2х сигналов Создание анимации для показания временных ошибок:
plot(t2,real(fsig_rx2),'m-'); [h(1), h(2)] = animatescattereye(tfsig_rx2,N,.1,N,'lin',-1); plot(t2,real(y),'b-'); animatescattereye(yy,N,.1,17,'lr',0); Часть №2 Разработка согласованного фильтра load sig25.yyy; plot(sig25) s=sig25(6400:6800); ss=s./(max(s)); ss=abs(ss); sss=ss; z=sum(ss.*sss); p=z./2 p = 17.6963 SNR=-30; SN=awgn(s,SNR,'measured',1234,'dB'); SN1=SN./(max(SN)); SN1=abs(SN1); z1=sum(SN1.*ss) z1 = 19.2462
Порог необходимо значительно повысить относительно p/2
Вывод:
- Основными параметрами глазковой диаграммы являются время фронта, время спада, коэффициент раскрытия глазка, высота и ширина глазка, относительная ширина места пересечения.
- При увеличении шума глаз больше “закрывается”.
- диаграмма рассеяния синфазной компоненты в сравнении с квадратурной компонентой сигнала, которая строится в соответствии с величиной выборки на символ, N. Результирующий график показывает принятый сигнал в соответствии с набором символов. Когда канал не зашумлен и при отстутствии помех, эти символы идентичны переданным. Лабораторная работа № 3 Лабораторная работа № 4 Лабораторная работа № 5 Листинг. Сверточное кодирование lab4 trel = poly2trellis([5 4],[23 35 0;0 5 13]); code = convenc(ss,trel); ncode = rem(code + randerr(576,1,[0 1;.95.05]),2); decoded = vitdec(ncode,trel,34,'cont','hard'); [number,ratio] = biterr(decoded(68+1:end),ss(1:end-68)) number =
ratio =
0.1614
osh=randerr(384,1,[0 1;0.95 0.05]); necode=rem(ss+osh,2); [number,ratio] = biterr(necode(68+1:end),ss(1:end-68))
number = ratio =
0.5285
Пунктурное кодировнаие lab4 t = poly2trellis(7,[171 133]); code = convenc(ss,t); tcode = -2*code+1; punctcode = tcode; punctcode(3:3:end)=[]; ncode = awgn(punctcode,8,'measured',1234); nicode = zeros(768,1); nicode(1:3:end) = ncode(1:2:end); nicode(2:3:end) = ncode(2:2:end); decoded = vitdec(nicode,t,96,'trunc','unquant'); [number,ratio]=biterr(decoded,ss)
number =
ratio = Контрольные вопросы:
Слово «сверточный» отражает от факт, что данные на выходе генерируются с помощью линейного сложения (т.е. «свертки») смещенных во времени импульсов последовательности на входе с импульсной характеристикой кодера (заполнения регистров предыдущими битами).
Иногда бывает так, что избыточность данных, обеспечиваемая сверточным кодером, при определенных условиях помеховой обстановки достаточна высока и является излишней, и встает задача уменьшить избыточность. Для этого можно, конечно, разработать соответствующий сверточный кодер, но целесообразнее добавить в схему блок, который будет просто уничтожать лишние биты. Процесс, выполняемый таким блоком, называется пунктурным кодированием.
Уничтожение лишних битов Лабораторная работа № 6
Лабораторная работа № 7
Модуляция цифровых сигналов
Цель работы: изучение принципов модуляции цифровых сигналов
Задание на выполнение работы: собрать с помощью библиотеки блоков Simulink схемы, реализующие различные виды модуляции цифровых сигналов, получить скрин-шоты результатов работы моделей.
Построение сигнального созвездия цифровой модуляции QPSK (квадратурной фазовой манипуляции) Вариант:
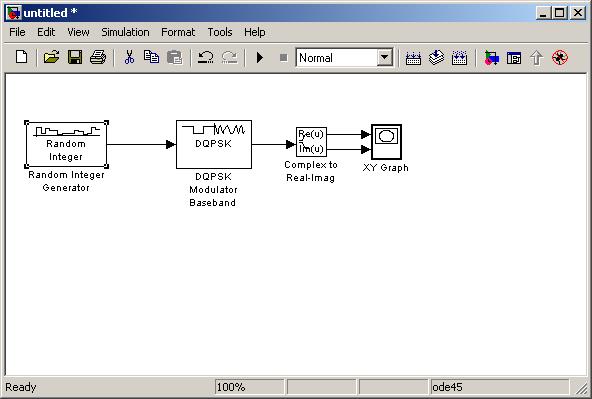
Рисунок 1. Модель для построения сигнального созвездия цифровой модуляции QPSK
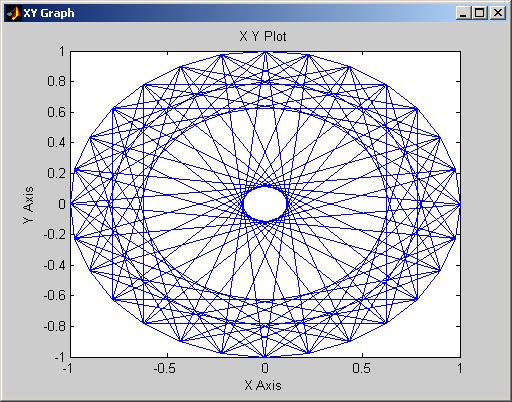
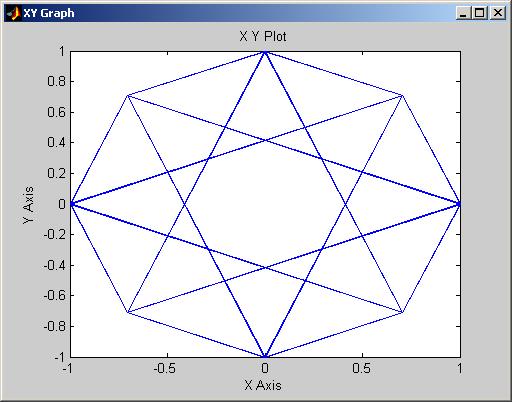
Рис.2 Сигнальное созвездие квадратурной фазовой манипуляции(
Рис.3 Сигнальное созвездие квадратурной фазовой манипуляции(
Построение сигнального созвездия цифровой модуляции QАМ (квадратурной амплитудной манипуляции) выполняется с помощью модели, схема которой приведена на рисунке 2.
Рисунок 4. Модель для построения сигнального созвездия цифровой модуляции QАМ
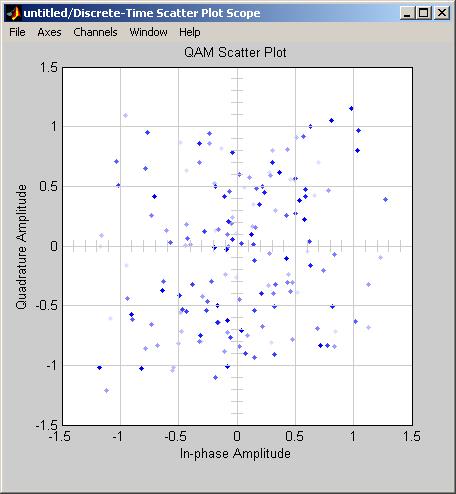
Рис.5 Диаграмма рассеяния. (Параметр Es/No= 8)
Рис.6 Диаграмма рассеяния. (Параметр Es/No= 1)
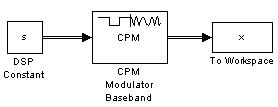
Схема модели построения дерева фаз СРМ представлена на рисунке 7.
Рисунок 7. Схема модели построения дерева фаз СРМ
% Параметры блока узкополосной модуляции CPM M_ary_number = 2; modulation_index = 2/3; pulse_length = 2; samples_per_symbol = 8; opts = simset('SrcWorkspace','Current',... 'DstWorkspace','Current');
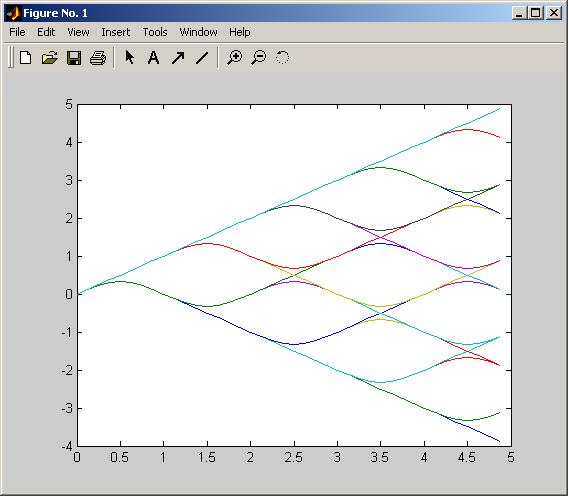
L = 5; % Количество показываемых символов pmat = []; for ip_sig = 0:(M_ary_number^L)-1 s = de2bi(ip_sig,L,M_ary_number,'left-msb'); % Отображение входных символов с помощью модуляции CPM % символ 0 -> -(M-1), символ 1 -> -(M-2), и т.д.. s = 2*s'+1-M_ary_number; sim('doc_phasetree',.9, opts); % запуск модели для получения результата «x» % построение следующего столбца переменной pmat pmat(:,ip_sig+1) = unwrap(angle(x(:))); end; pmat = pmat/(pi*modulation_index); t = (0:L*samples_per_symbol-1)'/samples_per_symbol; plot(t,pmat); figure(gcf); %
Рис.8 График дерева фаз
Построение модели полосового цифрового модулятора
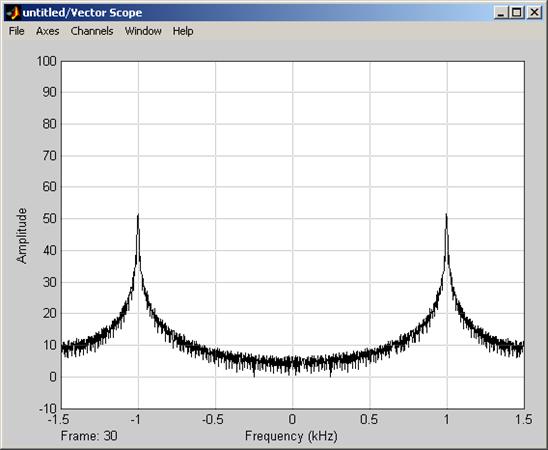
Рисунок 9. Модель полосовой многофазовой манипуляции
Рис.9 График спектра модулированного сигнала.(блок M-PSK Modulator Passband)
Рис.10 График спектра модулированного сигнала. (блок M-DPSK Modulator Passband)
Рис.11 График спектра модулированного сигнала (блок OQPSK Modulator Passband)
Контрольные вопросы: 1. Как изменяется вид сигнального созвездия при изменении значения скачка фазы при модуляции QPSK? Число “лепестков” созвездия измениться. При увеличении фазу их число уменьшиться 2. Что такое код Грея и для чего он используется? Код Грея — система счисления, в которой два соседних значения различаются только в одном разряде. Наиболее часто на практике применяется рефлексивный двоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея для систем счисления с любым основанием. В большинстве случаев, под термином «код Грея» понимают именно рефлексивный бинарный код Грея. Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.
Лабораторная работа № 8
Лабораторная работа № 1 Проектирование аналоговых и цифровых фильтров
Цель работы: изучение реализации процесса выборки с запасом и расчета параметров аналоговых и цифровых фильтров. Задание на выполнение работы: Разработать аналоговый и цифровой фильтр для параметров сигнала. Параметры сигнала:
Р, дБ = -57
Расчетная дискритизация = 20500 Гц, но мы её увеличиваем до 25000 по модели построения фильтра
Рисунок 1. Схема для тестирования разработанного фильтра
a=abs(fft(xcov(yout))); f = 25000*(0:10001)/20002; plot(f(1:10001),a(1:10001));
Рисунок 2. Спектр выходного сигнала
Рисунок 3. Одна из секций разработанного фильтра
Вывод:
- Получится фильтр из меньшего числа секций
- Получится фильтр из большего числа секций
Лабораторная работа № 2
|
|||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.50.169 (0.008 с.) |

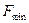 , кГц = 0,05
, кГц = 0,05 , кГц = 10
, кГц = 10 , кГц = 0,5
, кГц = 0,5 =20500 Гц
=20500 Гц













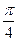 )
)