
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отношения между понятиями. Круги эйлера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
По содержанию между понятиями могут быть два основных вида отношений: сравнимость и несравнимость. Понятия, имеющие в своих содержаниях общие признаки, называются СРАВНИМЫМИ («адвокат» и «депутат»; «студент» и «спортсмен»). В противном случае, понятия считаются НЕСРАВНИМЫМИ («крокодил» и «блокнот»; «человек» и «пароход»). Если кроме общих признаков понятия имеют и общие элементы объёма, то они называются СОВМЕСТИМЫМИ. Существует шесть видов отношений между сравнимыми понятиями. Отношения между объёмами понятий удобно обозначать с помощью кругов Эйлера (круговые схемы, где каждый круг обозначает объём понятия).
15. Простой категорический силлогизм. Силлогизм — это выведение следствия, заключения из определенных посылок. Силлогизм, посылками в котором являются категорические суждения, называется категорическим. Посылок в силлогизме две. Они содержат три термина силлогизма, обозначаемые буквами S, P и М. Р — это больший термин, S — меньший, М — средний, связующий. Пример категорического силлогизма. Все боксеры — спортсмены. Этот человек — боксер. Этот человек — спортсмен. Слово «боксер» здесь является средним термином, первая посылка — больший термин, вторая — меньший. Во избежание ошибок заметим, что в данном силлогизме имеется в виду данный, конкретный человек, а не все люди. В противном случае, конечно, вторая посылка была бы намного шире по объему. Категорический силлогизм имеет четыре формы в зависимости от положения в его структуре среднего термина. * В первом случае большая посылка должна быть общей, а меньшая — утвердительной. * Вторая форма категорического силлогизма дает отрицательное заключение, и одна из его посылок также отрицательна. Большее понятие, как и в первом случае, должно быть общим. * Заключение третьей формы должно быть частным, меньшая посылка – утвердительной. * Четвертая форма категорических силлогизмов из таких умозаключений нельзя вывести общеутвердительное заключение, а между посылками существует закономерная связь. Так, если одна из посылок отрицательная, большая должна быть общей, при этом меньшая должна быть общей, если большая — утвердительна.
16. Выделяющие и исключающие суждения.
17. Логика как наука. Слово "логика" для обозначения науки о мышлении, о формах и законах его, ввел в самом начале III в. до н.э. основатель стоического направления в философии – Зенон. Как известно, Аристотель (384--322 гг. до н. э.), подлинный создатель логики как науки, пользовался для ее обозначения словом «аналитика». Скорее всего, слово «логика» происходит от древнегреческого «логос», которое еще тогда представляло собой крайне многозначное выражение, являющееся основополагающим для философских взглядов многих античных философов. Многозначность логоса отразилась и на значении слова «логика». «Логос» — это и понятие, слово, мысль, разум, идея, принцип, закон, порядок и пр. Логика как одна из наук о мышлении, философски окрашенная наука. Это - наука о структуре форм мысли, о простейших мыслительных методах, о законах связи форм мысли между собой, а также и об ошибках, возможных при нарушении этих законов. В отличие от других наук, изучающих мышление, логика изучает особенности, свойства форм мысли, отвлекаясь при этом от того конкретного содержания, которое могут нести эти формы мысли; она изучает их со стороны строения, структуры, т. е. внутренней закономерной связи составляющих форму мысли элементов.
18. Сложные и сокращенные силлогизмы.
19. Распределенность терминов в суждениях. Распределенность терминов в суждениях. Разделяя суждения на общие и частные, мы обращали внимание только на количественную характеристику субъекта (т.е. на количество предметов, о которых говорится в суждении). Но можно пойти дальше и исследовать количественную характеристику предиката. Для характеристики соотношения объемов субъекта и предиката используется понятие «распределенность термина». Термин считается распределенным, если его объем полностью включается в объем другого термина или полностью исключается из него. Термин считается нераспределенным, если его объем, лишь частично включается в объем другого термина или частично исключается из него.
20. Сокращенный силлогизм. В мышлении мы оперируем понятиями, суждениями и умозаключениями, в том числе и силлогизмами. Когда говорится о сокращенных силлогизмах, имеется в виду, что в таком умозаключении пропущена одна из посылок, а в некоторых случаях — заключение. Все птицы имеют крылья. Все чайки — птицы. Все чайки имеют крылья. Это пример простого категорического силлогизма. Для того чтобы получить сокращенный силлогизм, можно опустить большую посылку, т. е. «все чайки имеют крылья». Таким образом, получим: «Все чайки являются птицами — значит, все чайки имеют крылья». Естественно, что в этом случае следствие силлогизма будет истинным. Другими словами, сокращение силлогизма не влияет на его истинность или ложность. Можно привести такой пример: «Все газы летучи, следовательно, кислород летуч». Это сокращенный силлогизм, а полный выражается следующим образом. Все газы летучи. Кислород — газ. Кислород летуч. В отличие от предыдущего примера здесь пропущена меньшая посылка
21. Закон торжества. Закон тождества (a є a). Чтобы дать его характеристику, прежде необходимо понять, что же такое тождество вообще. В наиболее общем смысле под тождеством понимают равнозначность, одинаковость. Закон тождества означает, что в процессе построения суждений, высказываний недопустимо подменять один предмет другим. То есть нельзя произвольно заменять предмет, с которого логическое построение было начато, на другой. Нельзя называть тождественными предметы, таковыми не являющиеся, и отрицать тождественность одинаковых предметов. Все это ведет к нарушению закона тождества. Также нарушение закона тождества происходит в случае, когда человек неправильно называет вещи. В этом случае он может передавать верную информацию, которая тем не менее не касается названного предмета. Зачастую закон тождества нарушается при использовании двусмысленных слов. Это могут быть местоимения, слова-омонимы. Говоря о законе тождества и его нарушениях, нужно назвать эти нарушения. Первое носит название «подмена понятия» и означает, что был потерян предмет понятия, т.е. первоначально понимаемое значение изменилось. Подмена тезиса — второй тип. Он означает изменение первоначально понимаемого тезиса в процессе дискуссии. Закон тождества широко используется не только в рамках логики, но и другими, в том числе и прикладными, науками: информатикой и математикой, юриспруденцией, криминалистикой и др.
22. Условно – разделительные умозаключения.
23. Сложные суждения. Сложные суждения — это суждения, созданные из двух простых. Конъюнкция (a^b) — это способ связи простых суждений в сложные, при котором истинность полученного суждения напрямую зависит от истинности составных. Истинность таких суждений достигается только тогда, когда оба простых суждения (и a, и b) так же истинны. Дизъюнкция (a Ъ b) бывает строгой и нестрогой. Отличие между этими двумя видами дизъюнкции состоит в том, что при нестрогом виде члены ее не исключают друг друга. Истинность подобного сложного суждения зависит от истинности его членов следующим образом: если ложны оба члена, ложным признается и образованное при их посредстве дизъюнктивное суждение. Однако, если ложно только одно простое суждение, такая дизъюнкция признается истинной. Эквивалентация характеризуется тем, что образованное сложное суждение истинно только в тех случаях, когда истинны оба простых суждения, входящих в его состав, и ложно при ложности обоих этих суждений. Импликация (a ® b) истинна во всех случаях, кроме одного. Другими словами, если оба входящих в импликацию простых суждения истинны или ложны либо если ложно суждение a, импликация истинна. Однако при ложности суждения b ложным становится и сама импликация.
24. Разделительно – категорические суждения.
25. Закон противоречия.
Закон противоречия — закон логики, который гласит, что два несовместимых (противоречащих) суждения не могут быть одновременно истинными. По крайней мере, одно из них ложно. Сущность закона противоречия: два несовместимых друг с другом суждения не могут быть одновременно истинными — по крайней мере, одно их них необходимо ложно. Требование закона противоречия выражает объективные свойства самих вещей. Закон противоречия распространяется только на несовместимые понятия. Данный закон имеет важную особенность: он действует в определенных границах и распространяется не на все суждения, а только на несовместимые. Несовместимыми называются суждения, которые одновременно не могут быть истинными. Несовместимость бывает двух видов: противоположная («самолет вылетает днем» — «самолет вылетает ночью») и противоречащая («Вы мне друг» — «Вы мне не друг». Кстати, это не означает, что «враг»). Из приведенных примеров видно, что данный закон только указывает на ложность одного из двух логически несовместимых суждений. Но какое их них будет ложным, закон противоречия не позволяет определить. Вопрос о том, какое из двух суждений истинно, а какое ложно, решается в процессе конкретного исследования и проверки на практике. Закон указывает лишь на то, что из истинности одного из несовместимых суждений с необходимостью следует ложность другого.
26. Алетическая модальность.
Модальность - это явно или неявно выраженная в суждении дополнительная информация о степени его обоснованности, логическом или фактическом статусе, о регулятивных, оценочных и др. его характеристиках. Слово с помощью которого фиксируется модальность высказывания называется модальным функтором, а высказывание содержащее модальный функтор называется модальным. Наиболее распространенными являются модальности: * алетическая (истина) выражается с помощью операторов (функторов) "необходимо", "возможно", "случайно". Основными алетическими понятиями принято считать понятия возможности и необходимости. Для выражения возможности в русском языке употребляются слова "возможно", "может быть", "вероятно" и др. Для выражения необходимости употребляются слова "необходимо", "должно быть", "следовательно" и др. * аксиологическая (ценный, оценочная ) модальность высказывания с точки зрения определенной системы ценностей. Аксиологический статус высказывания выражается абсолютными ("хорошо", "плохо", "неплохо", "безразлично") или относительными ("лучше", "хуже", "равноценно") оценочными понятиями. * деонтическая (как должно быть) модальность отражает связь утверждаемого в суждении с нормами морали, права, конкретными обязательствами ("должен", "обязан", "может", "допустимо", "запрещено", "разрешено"), а также может выражать приказ, побуждение к определенным действиям. * эпистемическая (достоверное знание) модальность отражает степень обоснованности содержания суждения в знании (от "доказано" или "опровергнуто" до "вероятно", "проблематично", "маловероятно" т. п.), а также способ принятия информации, содержащейся в суждении ("знаю", "верю", "убежден", "сомневаюсь" и т.п.).
27. Логические отношения между суждениями. Элементами структуры понятия выступают его содержание и объем. Содержание понятия отражает совокупность существенных признаков предметов мысли, на основании которых они выделяются и обобщаются в данном множестве. В свою очередь содержание понятия включает в себя родовые и видовые признаки. Родовой признак - это такой признак, который является общим для предметов более обширного множества (рода), из которого было выделено данное (вид). Видовой признак - это такой признак, на основании которого данное множество предметов мысли (вид) было выделено из более обширного (род). Напр, в содержание понятия "озеро" входит родовой признак "быть водоемом" и видовые: "иметь естественное происхождение", "быть замкнутым". Объем понятия отражает множество предметов мысли, которые обладают признаками, составляющими удержание данного понятия. Объем понятия включает в себя следующие элементы: род, вид, индивид. Род есть полное множество предметов, мыслимых в данном понятии. Вид есть выделенная по какому-либо признаку из полного множества частная совокупность предметов, мыслимых в данном понятии. Индивид есть отдельно взятый единичный предмет, мыслимый в данном понятии. Нап: озеро (род) - озеро соленое (вид); озеро Иссык-Куль (индивид). Содержание и объем понятия взаимосвязаны логическим законом обратного соотношения объема и содержания понятия: увеличение содержания понятия, т.е. числа существенных признаков, ведет к уменьшению его объема, т.е. совокупности предметов, мыслимых в данном понятии, и наоборот. Этот закон справедлив только для сравнимых понятий.
28. Операции с классами. Операции с классами — это такие логические действия, которые приводят нас к образованию нового (в общем случае) класса.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 5562; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.208.243 (0.009 с.) |

 1) А – Аристотель В – основатель логики 2) А – квадрат В – равносторонний прямоугольник
1) А – Аристотель В – основатель логики 2) А – квадрат В – равносторонний прямоугольник
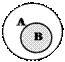 1) А – человек В – студент 2) А – животное В – слон
1) А – человек В – студент 2) А – животное В – слон
 1) А – юрист В – депутат 2) А – студент В – спортсмен
1) А – юрист В – депутат 2) А – студент В – спортсмен
 1) А – животное В – кот; С – собака; D – мышь 2) А – драгоценный металл В – золото; С – серебро; D - платина
1) А – животное В – кот; С – собака; D – мышь 2) А – драгоценный металл В – золото; С – серебро; D - платина
 1) А – белый кот; В – рыжий кот (коты бывают и чёрными и серыми) 2) А – горячий чай; холодный чай (чай может быть и тёплым) Т.е. понятия А и В не исчерпывают всего объёма понятия, в которое они входят.
1) А – белый кот; В – рыжий кот (коты бывают и чёрными и серыми) 2) А – горячий чай; холодный чай (чай может быть и тёплым) Т.е. понятия А и В не исчерпывают всего объёма понятия, в которое они входят.
 1) А – высокий дом В – невысокий дом 2) А – выигрышный билет В – невыигрышный билет Т.е. понятия А и не-А исчерпывают весь объём понятия, в которое они входят, так как между ними нельзя поставить никакое дополнительное понятие.
1) А – высокий дом В – невысокий дом 2) А – выигрышный билет В – невыигрышный билет Т.е. понятия А и не-А исчерпывают весь объём понятия, в которое они входят, так как между ними нельзя поставить никакое дополнительное понятие.



