
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка выдвинутой гипотезы О законе распределения исходных данных с доверительной вероятностью 0,95 по критерию пирсонаСодержание книги
Поиск на нашем сайте Используем для проверки критерий согласия Пирсона (критерий
Далее по статистическим таблицам критических точек распределения Причем число степеней свободы определяется с учетом числа интервалов и числа связей, наложенных на заданное значение:
Найденное значение 1)если 2)если При этом существует вероятность
i – номер интервала;
yi – нормирующие случайные величины относительно найденного среднего; Ф(уi) – функция Лапласа от нормирующего значения yi; Рi – теоретическая вероятность попадания в i – тый интервал.
Таблица 3 Определение
Исходя из того, что:
Гипотеза о том, что представленный закон распределения является нормальным принимается.
Понятие интервальных оценок, оценка доверительного интервала результата измерений и представление его в соответствии с ГОСТ Точечные оценки параметров закона распределения являются случайными, поэтому для них необходимо определить доверительный интервал. Интервальной называется оценка, которая определяется двумя числами, покрывающими оцениваемый параметр. Доверительный интервал — это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью. Интервальная оценка математического ожидания определяется следующим образом, если исходная выборка распределена по нормальному закону, то можно показать, что оценка математического ожидания в виде среднего имеет дисперсию:
Если при проведении измерительного эксперимента возможно малое число наблюдений или закон распределения неизвестен, то оценка математического ожидания и СКО математического ожидания принимаются равными вычисленным оценкам. При заданной доверительной вероятности можно установить величину доверительного интервала для
Р = (0,9…0,95)
При малом объеме выборки используем Таким образом, доверительный интервал оценки истинного значения мат ожидания:
В соответствии с ГОСТ результат многократных измерений записывается:
Оценка погрешности от смещенности Погрешность от смещенности:
Определение минимально необходимого количества измерений
При выполнении многократных измерений с заданной точностью и достоверностью возникает проблема определения необходимого количества измерений. В качестве характеристики точности обычно задается допустимое отклонение параметра от истинного значения.
Следовательно, допустимое отклонение не должно превышать этого значения, отсюда
Изначально зададим, что допустимое отклонение
Закон распределения известен и вместо коэффициента Стьюдента Необходимо провести минимум 86 измерений.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Батищева О.М. «Общая теория измерений»: электронное пособие. 2. Грановский В.А., Сирая Т.Н. «Методы обработки экспериментальных данных при измерениях». 3. Дунин – Барковский «Взаимозаменяемость, стандартизация и технические измерения», 1986г. 4. Назаров Н.Г. «Метрология. Основные понятия и метрологические модели» 5. Сергеев, Крохин «Метрология» 6. Тартаковский Д.Ф., Ястребов А.С., «Метрология, стандартизация и технические средства измерений». 7. Нефедов «Электрорадиоизмерение». 8. Ганевский и др. «Допуски, посадки и технические измерения».
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 ). Для того, чтобы проверить нулевую гипотезу
). Для того, чтобы проверить нулевую гипотезу 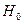 , необходимо вычислить теоретические частоты и наблюдаемое значение
, необходимо вычислить теоретические частоты и наблюдаемое значение  , которое является мерой расхождения данных от теоретического закона:
, которое является мерой расхождения данных от теоретического закона:
 - теоретическая частота (вероятность) попадания в i - тый интервал.
- теоретическая частота (вероятность) попадания в i - тый интервал. и числу степеней свободы
и числу степеней свободы  необходимо найти критическую точку
необходимо найти критическую точку 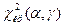 и сравнить ее с наблюдаемым значением.
и сравнить ее с наблюдаемым значением.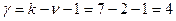
 - число оцениваемых параметров, равное 2.
- число оцениваемых параметров, равное 2. - число связей, равное 7.
- число связей, равное 7. сравниваем с наблюдаемым значением
сравниваем с наблюдаемым значением  нет оснований отвергать гипотезу о распределении выборки по нормальному закону;
нет оснований отвергать гипотезу о распределении выборки по нормальному закону;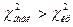 , гипотеза отвергается.
, гипотеза отвергается.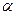 ошибочного принятия нулевой гипотезы, или ошибочного ее отвержения.
ошибочного принятия нулевой гипотезы, или ошибочного ее отвержения. - нижняя граница интервала;
- нижняя граница интервала; - верхняя граница интервала;
- верхняя граница интервала; - середина середина i – того интервала;
- середина середина i – того интервала;
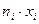
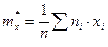 =11,105
=11,105



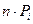

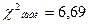
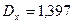
 =1,182
=1,182


 ,
,
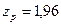 - квантиль распределения Лапласа
- квантиль распределения Лапласа
 =2 - коэффициент распределения Стьюдента.
=2 - коэффициент распределения Стьюдента.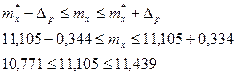






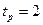 , используется квантиль распределения Лапласа
, используется квантиль распределения Лапласа 


