
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додавання гармонічних коливань. Биття.Содержание книги
Поиск на нашем сайте x1=A1cos(wt+φ1) x2=A2cos(wt+φ2) x=x1+x2 A^2=A1^2+A2^2+2*A1*A2cos(φ2- φ1) tg φ=(A1*sinφ1+A2*sinφ2)/(A1*cosφ1+A2*cosφ2) Особливий випадок додавання гармонічних коливань в одному напрямку, це коли їх частоти незначно відрізняються w1≈w2 x=2A*cos((w1+w2)/2)*t*cos(w1-w2)/2=2A*cos* дельтаW/2 * t*cosw*t нехай додають два коливання x=A*coswt y=B*cos(wt+φ) y/B=coswt*cosφ-sinwt*sinφ x/A=coswt sin^2(φ)=x^2/A^2-2(x/A)*(y/B)+y^2/B^2
x/A-y/B=0 y=Bx/A
y=-Bx/A -рівняння прямої
x^2/A^2+ y^2/B^2 =1 -рівняння еліпса
якщо при взаємно перпендикулярних коливаннях частоти співвідносяться як ½,2/3,1/4…, то ми отримаємо фігури Лісажу. Биття́ — інтерференція двох звукових коливань, з частотами Різниця фаз таких коливань з часом змінюється, через що фази періодично збігаються (коливання підсилюють одне одне) або стають протилежними (коливання взаємно ослаблюються). Підсилення і ослаблення результативних коливань відбуваються періодично з частотою
3. Фізи́чний МатематичнийПружинний маятник
Період коливань фізичного маятника визначається формулою
Зведена довжина фізичного маятника - довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника. Вона дорівнює
Математичний маятник
Математичний маятник має два положення рівноваги: стійке та нестійке. В стійкому положенні рівноваги маятник висить непорушно строго вертикально, сила тяжіння врівноважується силою пружності стержня. Інше положення рівноваги математичного маятника знаходиться в точці Рівняння руху Нехай маятник відхилився від положення рівноваги на кут θ між вертикаллю й стержнем Потенціальна енергія математичного маятника дорівнює
де Кінетична енергія в будь-який момент часу t визначається моментом інерції I та кутовою швидкістю ω:
Момент інерції матеріальної точки масою m відносно осі, яка проходить перпендикулярно до площини рисунка через точку підвісу, дорівнює
Функція Лагранжа математичного маятника для узагальненої координати θ дорівнює
Рівняння Лагранжа
визначає рівняння руху маятника
Період коливань математичного маятника залежить від амплітуди, тобто від початкового відхилення. Але навіть при відхиленні на 60° відхилення частоти від формули, наведеної для малих коливань, не перевищує 15%.
Коливання такого маятника відбувається під дією сили пружності, отже, на відміну від математичного, пружинний маятник може бути розташований і горизонтально.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 1) φ=2mπ. m=0,1,2..
1) φ=2mπ. m=0,1,2..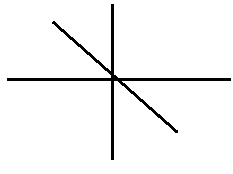 2) φ=(2m+1)π
2) φ=(2m+1)π 3) φ=(2m+1)π/2
3) φ=(2m+1)π/2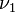 і
і  настільки близькими, що вони не сприймаються як два роздільні коливання. Амплітуда коливань, які виникають при цьому періодично збільшується чи зменшується у часі з частотою, рівною різниці інтерферуючих коливань.
настільки близькими, що вони не сприймаються як два роздільні коливання. Амплітуда коливань, які виникають при цьому періодично збільшується чи зменшується у часі з частотою, рівною різниці інтерферуючих коливань. , що дорівнює різниці частот взаємодіючих коливань, тобто
, що дорівнює різниці частот взаємодіючих коливань, тобто  . В акустиці биття використовуються для порівняння тонів (наладнання муз. інструментів). Якщо різниця частот коливань двох джерел дуже мала (напр., менша ніж 0,1 Гц), то вухо сприймає їх як один результативний тон, інтенсивність якого змінюється з частотою, рівною
. В акустиці биття використовуються для порівняння тонів (наладнання муз. інструментів). Якщо різниця частот коливань двох джерел дуже мала (напр., менша ніж 0,1 Гц), то вухо сприймає їх як один результативний тон, інтенсивність якого змінюється з частотою, рівною  . Коли частоти складових коливань зближуються, то частота биття зменшується і при
. Коли частоти складових коливань зближуються, то частота биття зменшується і при  . Якщо порівнювати тони методом биття, то похибка може не перевищувати 0,1 Гц. В електромагнітних коливаннях явище биття використовується в чутливих приймачах радіосигналів та вимірювальних приладах.
. Якщо порівнювати тони методом биття, то похибка може не перевищувати 0,1 Гц. В електромагнітних коливаннях явище биття використовується в чутливих приймачах радіосигналів та вимірювальних приладах. Фізи́чний ма́ятник — тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить через центр маси тіла.
Фізи́чний ма́ятник — тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить через центр маси тіла.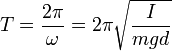 , де I - момент інерції, m - маса, d - віддаль від центра маси тіла до осі, g - прискорення вільного падіння.
, де I - момент інерції, m - маса, d - віддаль від центра маси тіла до осі, g - прискорення вільного падіння.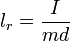 .
.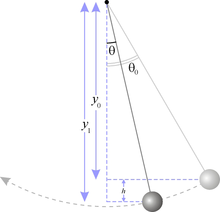 Математи́чний ма́ятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена на невагомому нерозтяжному стержні довжини l і здійснює рух в вертикальній площині під впливом сил тяжіння з прискоренням вільного падіння g.
Математи́чний ма́ятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена на невагомому нерозтяжному стержні довжини l і здійснює рух в вертикальній площині під впливом сил тяжіння з прискоренням вільного падіння g.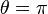 , тобто коли стержень орієнтований вертикально вгору. В цьому положенні сили тяжіння та пружності стержня, як і в точці стійкої рівноваги, зрівноважені, проте дана рівновага є нестійкою.
, тобто коли стержень орієнтований вертикально вгору. В цьому положенні сили тяжіння та пружності стержня, як і в точці стійкої рівноваги, зрівноважені, проте дана рівновага є нестійкою. ,
, - висота відносно найнижчого положення.
- висота відносно найнижчого положення. .
. .
. .
.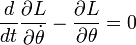
 .
.
 Пружинний маятник складається з тягарця масою m, з’єднаного з пружиною жорсткістю k. Якщо зовнішньою силою вивести систему з положення рівноваги, вона може коливатися відносно положенняO.
Пружинний маятник складається з тягарця масою m, з’єднаного з пружиною жорсткістю k. Якщо зовнішньою силою вивести систему з положення рівноваги, вона може коливатися відносно положенняO. 


