
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные правила по технике безопасностиСодержание книги
Поиск на нашем сайте
ДЕТАЛИ МАШИН Лабораторные работы Минск 2008 Министерство образования Республики Беларусь БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Детали машин,
ДЕТАЛИ МАШИН
Лабораторные работы по дисциплинам «Детали машин и подъемно-транспортные машины», «Детали машин и основы конструирования», «Прикладная механика»
Под редакцией А.Т. Скойбеды
Минск 2008 УДК 621.8 (076.5) ББК 34.44я7 Д 38
Составители: А.Т. Скойбеда, А.В. Кузьмин, В.Л. Николаенко, В.М. Анохин, В.В. Бирич, А.Г. Бондаренко, В.Д. Василёнок, А.А. Зенькович, В.Ф. Калачёв, А.А. Калина, И.М. Комяк, Т.Н. Микулик, Н.Н. Розанова, В.И. Шпилевский, И.В. Швец
Рецензенты: В.А. Балицкий, О.Г. Девойно
Данное издание предназначено для студентов, выполняющих лабораторные работы по дисциплинам «Детали машин» и «Прикладная механика». В нем приведены описания лабораторных установок, методика проведения работ, рекомендации по оформлению отчетов и контрольные вопросы.
ISBN 978-985-479-725-0 © БНТУ, 2008 Введение
Данное издание является пособием по дисциплинам «Детали машин и подъемно-транспортные машины» и «Детали машин и основы конструирования» для студентов машиностроительных специальностей и может быть использовано при выполнении лабораторных работ по дисциплине «Прикладная механика». В настоящее время усилена физико-математическая подготовка студентов, техническое образование приобретает университетскую направленность, в учебные планы введены дисциплины по изучению методов научных исследований и т.д. В связи с этим роль лабораторных работ в учебном процессе существенно возрастает. Лабораторные занятия следует рассматривать как наиболее действенное практическое средство обучения, в процессе которого студенты должны приобретать навыки для выполнения научных исследований. Поэтому основными задачами лабораторных работ являются экспериментальное подтверждение теоретических выводов, полученных при изучении лекционного материала; развитие навыков, привычек и способностей к самостоятельному выполнению необходимых действий с приборами и установками; приобретение навыка практической оценки результатов опытов; глубокое изучение физической сущности функционирования различных деталей и узлов машин и методик выполнения работ, имеющих различный характер; использование методик обработки опытных данных; обобщение полученных результатов и оценка возможных ошибок.
В издании освещаются методика и порядок выполнения работ, даются описания, чертежи (схемы) установок, приводятся образцы отчетов по каждой работе, кратко рассматриваются теоретические вопросы, практическая проверка которых составляет предмет лабораторных исследований. При этом авторы стремились трактовку и терминологию этих вопросов увязать с действующими стандартами и учебниками по деталям машин. Объем и методика лабораторных работ рассчитаны так, чтобы каждая из них выполнялась в течение двух академических часов. При этом предусматривается предварительная подготовка студентов к выполнению задания. На ряд вопросов, поставленных в конце каждой работы, в отчетах студенты должны поместить обстоятельные ответы, иллюстрированные необходимыми чертежами, схемами, расчетами. Методики проведения лабораторных работ разработаны сотрудниками кафедры «Детали машин, подъемно-транспортные машины и механизмы» Белорусского национального технического университета. Кафедра «Детали машин, подъемно-транспортные машины и механизмы» выражает благодарность студентам автотракторного факультета Петрову Д.А., Хорликову М.Г., Снытко А.В., Павловскому В.С. за помощь в оформлении рукописи данного издания.
МЕТОДИКА ОБРАБОТКИ
В практике экспериментальных исследований часто встречаются случаи, когда при одних и тех же условиях не удается получить одинаковые результаты опытов. В результате каждого измерения получается некоторое число. Предсказать, какое именно число получится при выполнении следующего измерения, чаще всего невозможно. В случае когда результат эксперимента произвольно изменяется от одного наблюдения к другому, о результатах говорят как о случайных величинах. Случайная величина может быть дискретной и непрерывной.
Соотношение, устанавливающее связь между значениями случайной величины и вероятностями этих значений, называют законом распределения случайной величины, который задается какой-либо функциональной зависимостью (функцией распределения случайной величины) или в виде таблицы. Часто бывает, что нужно описать функцию распределения некоторой случайной величины в общих чертах с помощью одного-двух параметров. Наиболее употребительной и наилучшей мерой, характеризующей значение случайной величины, является среднее значение М(x). Определим среднее значение для непрерывной величины согласно формуле
где x – случайная величина распределения; f(x) – функция плотности непрерывной случайной величины. В случае дискретной случайной величины
где pi – вероятность значения xi. Если вероятности всех xi равны, то
где n – число значений x. Тогда выражение (1) запишется в следующем виде:
Кроме среднего значения функцию распределения случайной величины можно еще характеризовать параметром, показывающим, насколько широко «разбросаны» значения случайной величины относительно среднего значения. Наиболее употребляемой мерой, характеризующей рассеивание случайной величины, является дисперсия:
Квадратный корень из дисперсии называется среднеквадратичным или стандартным отклонением:
Чтобы сравнить рассеяние различных случайных величин, вычисляют относительное стандартное отклонение или коэффициент вариации
Коэффициент вариации характеризует колебательность ряда измерений. На результат измерения могут оказывать влияние различные факторы. Это влияние проявляется в виде ошибки, которая накладывается на значения измеряемой величины так, что результат измерения представляет собой сумму истинного значения измеряемой величины и ошибки. Все ошибки принято делить на две большие группы: систематические и случайные ошибки. Случайной называется ошибка Δ, которая изменяется от одного измерения к другому произвольно и в равной степени может быть как положительной, так и отрицательной. Случайная ошибка вызывается чаще всего одновременным действием различных факторов, например: изменением температуры, влажности и давления воздуха, толчками и вибрациями, колебаниями напряжения и частоты питающей сети, люфтами в сочлененных механических деталях и т.п. Влияние случайных ошибок на результат измерения может быть уменьшено обработкой экспериментальных данных методами теории вероятностей. Если интересующую нас величину измерить несколько раз и вычислить ее среднеарифметическое значение, то случайная погрешность этого среднего значения будет меньше, чем погрешность единичного измерения. Однако если известно, что определяющей является систематическая погрешность, то следует ограничиться единичным измерением. Систематической называется погрешность, значение которой при повторных измерениях остается постоянным или изменяется по определенному закону, зависящему от вызывающего ее фактора. К систематическим ошибкам относятся инструментальные ошибки, ошибки, вызванные методикой постановки эксперимента, и др.
Так как при выполнении измерений невозможно определить истинное значение измеряемой величины, в метрологии было введено понятие о ее действительном значении. Действительным условились называть такое значение измеряемой величины, в котором отсутствуют систематические погрешности, а случайные погрешности сведены к минимуму. правильность, характеризуемая систематическими погрешностями, и точность определяют достоверность измерений. Точность определяется случайными погрешностями и оценивается средней погрешностью ряда измерений. Мерой точности измерений служит относительная ошибка среднего арифметического:
Средняя квадратическая погрешность результата измерений или среднего арифметического определяется по формуле
На основании «правила трех сигм» можно заключить, что случайная величина, подчиняющаяся нормальному закону распределения, находится в следующих пределах:
В качестве примера рассмотрим расчет погрешности при определении величины тормозного момента. В результате эксперимента было получено восемь значений показаний индикатора. Вычисления приведены в таблице.
Величина тормозного момента определяется по формуле
где M(x) – регистрируемая величина, мм (делений); μ x – масштаб величины x (берется из тарировочного графика). Примем μ x = 1 Н Так как тормозной момент M топределяется произведением двух величин, которые имеют погрешность измерения, то необходимо оценить общую погрешность. Среднеквадратическая погрешность масштабного коэффициента для потенциометрических датчиков, тензодатчиков, датчиков угловой скорости обычно не превышает 1–2 %. Примем σµ x = 2 % = 0,02Н·м. Среднюю квадратическую ошибку значений тормозного момента можно определить по формуле
которую можно переписать в виде
тогда
Таким образом, действительное значение тормозного момента будет отличаться от среднего на величину 3 ·
и в нашем случае при восьми опытах
тогда
Основные правила по охране труда
1. К работе допускаются студенты, изучившие инструкцию по охране труда при выполнении работ в лаборатории, прошедшие инструктаж и расписавшиеся в журнале инструктажа по охране труда.
2. Перед началом работы необходимо ознакомиться с основными правилами по охране труда, изложенными в описании каждой лабораторной работы. 3. Выполнение лабораторных работ осуществляется под руководством и наблюдением преподавателя.
Лабораторная работа № 1
ИСПЫТАНИЕ БОЛТОВОГО СОЕДИНЕНИЯ,
Цель работы 1. Теоретическое и экспериментальное определение зависимости сдвигающей силы Fr от момента завинчивания Т зав. 2. Построение графиков зависимости Fr = f(Т зав ) по теоретическим и экспериментальным данным.
Общие сведения В настоящей работе изучается болтовое соединение, нагруженное силой, сдвигающей детали в стыке. Болт установлен в отверстие с зазором Δ (рис. 1.1) и подвергается предварительной затяжке, в результате которой между деталями возникают силы трения, препятствующие сдвигу деталей (раскрытию стыка).
     
Рис. 1.1. Схема нагружения соединения Момент завинчивания гайки, который нужно приложить к ключу (см. рис. 1.1):
где Т р – момент сил трения в резьбе; T т– момент сил трения на опорном торце гайки. В развернутом виде
где f т – коэффициент трения на торце гайки. Для условий опыта (сравнительно гладкие поверхности торца гайки и детали при наличии следов смазки) можно принять f т = 0,2; β – угол подъема винтовой линии на среднем диаметре, определяемый по уравнению
Здесь р и d 2соответственно шаг и средний диаметр резьбы, для опыта принимаемые из табл. 1.1.
Таблица 1.1
Геометрические параметры резьбы (ГОСТ 24705-81)
Окончание табл. 1.1
Средний диаметр опорной кольцевой площадки
Здесь D 1 – наружный диаметр опорного торца гайки, равный размерузева ключа; d 0 – диаметр отверстия под болт (см. рис. 1.1). D 1и d 0следует получить непосредственным измерением. Приведенный коэффициент трения в резьбе
где f р – действительный коэффициент трения в резьбе. Для условий опыта принять f р = 0,15. Угол профиля метрической резьбы α = 60°. Приведенный угол трения φ1= arctg f 1. Наименьшая сила затяжки определяется по уравнению
где Fr – сдвигающая сила (см. рис. 1.1); f 0 – коэффициент трения между соединяемыми деталями; его можно принять 0,15…0,2 при шероховатости поверхностей Ra = 2,5 со следами смазки; i – число стыков (поверхностей трения). Сопоставляя уравнения (1.1) и (1.2), получим
или иначе
где
На величину момента завинчивания T завсущественное влияние оказывают коэффициенты трения в резьбе и на торце гайки. Эти коэффициенты зависят от материала трущихся поверхностей и их шероховатости, наличия смазки и загрязнений и т.д. Поэтому теоретическое значение T завне всегда отвечает его действительной величине, определяемой экспериментальным путем. В практике знание величины T завчасто необходимо, например, для проектирования и настройки динамометрических ключей. Для предотвращения остаточных деформаций, которые могут возникнуть в стержне болта, необходимо ограничить силу затяжки. Эта сила определяется исходя из условия прочности стержня болта на одновременное растяжение и скручивание по уравнению
Для болта, изготовленного из стали Ст 3, принимаем σт = 220 МПа,коэффициент безопасности n = 2 и 1,3 – коэффициент, учитывающий скручивание тела болта. Тогда допускаемое напряжение
Для болта М16 d 3 = 14,160 мм (см. табл. 1.1):
Этому значению [ F зат]отвечает максимально допустимый момент завинчивания, определяемый по уравнению (1.1). Экспериментальное значение силы Fr может быть определено по уравнению
где n − число делений индикатора динамометра. Описание установки
Для исследования болтового соединения применяются испытательная машина ДМ 30 М (рис. 1.2) и приспособление ДМ 23 М Машина имеет механизм установочного (ускоренного) сближения наконечника 1, закрепленного на динамометрическом кольце 3, с упором 8, закрепленным в колодке приспособления ДМ 23 М. Механизм состоит из маховика 6, винтовой пары 4, смонтированной в поперечине 5, и штока 7, с которым динамометр соединен при помощи захвата и болта. Нагружение болтового соединения производится посредством червячного редуктора 10 и грузового винта 11 поворотом маховика 12. Приспособление ДМ 23 М состоит из основания, двух щек 13, болта с гайкой 15, ползуна 14 и упора 8.
Рис. 1.2. Испытательная машина ДМ30М: 1 – наконечник; 2 – индикатор; 3 – кольцо динамометрическое; В начальном положении ползун устанавливается так, чтобы его риска совпадала с верхней риской пластины. Опускание ползуна ниже нижней риски на пластине недопустимо, так как при этом выбирается зазор Δ и болт будет работать на срез. Для завинчивания гайки применяется динамометрический ключ с предельным моментом Т зав= 100 Н∙м.
Порядок выполнения работы 1. по указанию преподавателя подобрать болт для испытуемого соединения. 2. Измерить наружный диаметр болта. Результат измерения согласовать с ГОСТ 24705-81 и записать в табл. 1.4 отчета. 3. Измерить наружный диаметр опорного торца гайки D 1и диаметр отверстия под болт d 0. Результаты измерений занести в табл. 1.4 отчета. 4. Записать в табл. 1.4 отчета исходные данные для теоретического определения силы сдвига Fr. 5. по формуле (1.3) вычислить значения силы Fr при Т зав = 20; 30; 40; 50; 60; 70; 80 H∙м. Результаты расчетов занести в табл. 1.2 отчета. 6. По полученным данным построить график зависимости 7. Собрать приспособление ДМ 23 М, установив болт ранее принятого размера. 8. Затянуть гайку болта динамометрическим ключом. Момент затяжки Т зав= 20 Н∙м. Рукоятку ключа поворачивать плавно и непрерывно до показания на шкале принятого момента затяжки. 9. вращением маховика 6 (см. рис. 1.2) выбрать установочный зазор. 10. Нагрузить соединение. С этой целью маховик 12 (см. рис. 1.2) вращать до тех пор, пока стрелка индикатора не остановится, а затем быстро переместится в обратном направлении. В этот момент сила сдвига Fr и силы трения в стыках уравновешиваются, происходит раскрытие стыка и соединение не воспринимает нагрузку, превышающую силу трения покоя. Показания индикатора, соответствующие T зав = 20 Н·м, занести в табл. 1.3 отчета. 11. Без снятия предыдущей затяжки повторить действия, Результаты опыта занести в табл. 1.3 отчета. 12. по формуле (1.5) вычислить значения Fr. Результаты вычислений занести в табл. 1.3 отчета. 13. По полученным данным построить график зависимости Образец оформления отчета
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Лабораторная работа № 1
ИСПЫТАНИЕ БОЛТОВОГО СОЕДИНЕНИЯ,
Цель работы: 1. Теоретическое и экспериментальное определение 2. Построение графиков зависимости
Работу выполнил: Ф.И.О. группа Работу принял:
Минск ____ Схема нагружения соединения
Таблица 1.2
Результаты расчета силы Fr по формуле (1.3)
Таблица 1.3
Результаты расчета силы Fr
Таблица 1.4
Исходные данные для теоретического определения силы
Окончание табл. 1.4
График зависимости Fr
Т зав Контрольные вопросы 1. Почему для крепежных изделий (болтов, винтов) применяются резьбы с треугольным профилем? 2. Как производится расчет болтов, нагруженных силой затяжки и крутящим моментом затяжки? 3. Как выражается условие нераскрытия стыка соединения, нагруженного поперечными силами (болты поставлены с зазором)? 4. Какова зависимость между осевой силой на винте и силой, момент которой скручивает винт? 5. Каково условие самоторможения винтовых пар?
Лабораторная работа № 2
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ТРЕНИЯ В РЕЗЬБЕ
Цель работы 1. Определение коэффициента трения в резьбе f p. 2. Построение графика зависимости f pот среднего давления на витках резьбы Pр . 3. Определение коэффициента трения на торце гайки f т. 4. Построение графика зависимости f тот удельного давления на торце гайки P т . 5. Установление зависимости
Общие сведения
Момент завинчивания гайки T зав преодолевает момент сил трения в резьбе Т ри на торце гайки Т т :
В развернутом виде уравнение имеет вид
где F зат – сила затяжки, Н(см. рис. 1.1 лабораторной работы № 1); D ср – средний диаметр опорной кольцевой площадки, мм; f т – коэффициент трения на торце гайки; d 2 – средний диаметр резьбы; β – угол подъема винтовой линии градус; φ1 – приведенный угол трения в резьбе, градус. В приспособлении для нагружения болтов под гайкой установлен упорный шарикоподшипник, момент трения в котором незначительный, поэтому T зав ≈ Т р. В таком случае возникающее в результате затяжки болта осевое усилие F зави момент Т рсвязаны уравнением
Здесь Из уравнения (2.1) определяем приведенный угол трения в резьбе:
Приведенный коэффициент трения в резьбе
Приведенный коэффициент трения
Угол профиля метрической резьбы
При испытании со специальной втулкой упорный шарикоподшипник в приспособлении не работает. Момент трения на торце гайки определяется как разность момента завинчивания и момента сил трения в резьбе:
Известно, что
отсюда коэффициент трения на торце гайки
Средний диаметр опорной кольцевой площадки
где D 1 – наружный диаметр опорного торца гайки, равный размеру зева ключа, мм; d 0 – внутренний диаметр опорной поверхности, равный отверстию под болт или диаметру отверстия в шайбе, мм. Допускаемая сила затяжки болта определяется по уравнению
где d 3 – внутренний диаметр болта по дну впадины, мм; [σр]– допускаемое напряжение на растяжение, МПа; 1,3 – коэффициент, учитывающий скручивание тела болта. Для болта, изготовленного из стали Ст 3, принимаем σт= 220 МПа и коэффициент безопасности n = 2, тогда
Среднее давление на витках резьбы
где z – число витков резьбы по высоте гайки; H – высота гайки. Давление на торце гайки
Описание установки Установка состоит из приспособления для нагружения болтов (рис. 2.1) и торсионного динамометрического ключа.
Рис. 2.1. Приспособление для нагружения болтов: 1 – болт испытуемый; 2 – гайка; 3 – втулка сменная; 4 – шарикоподшипник упорный; 5 – динамометрическая пружина; 6 – сухарь стопорный; 7 – шайба сферическая; 8 – индикатор
Испытуемый болт 1 устанавливается в приспособление для нагружения болтов (см. рис. 2.1). Затяжка гайки 2 испытуемого болта производится торсионным динамометрическим ключом. Крутящий момент измеряется индикатором. В корпусе приспособления помещена динамометрическая пружина 5, позволяющая определить силу на болте по его деформации. Усилие затяжки болта 1 передается При определении коэффициента трения в резьбе гайка 2 опирается через втулку 3 и упорный шарикоподшипник 4 на динамометрическую пружину. Таким образом трение на торце гайки исключается. При определении коэффициента трения на торце гайки втулка 3 заменяется другой специальной втулкой. В этом случае упорный шарикоподшипник не работает.
Порядок выполнения работы
1. Выбрать исследуемый болт. 2. Измерить наружный диаметр болта d, шаг резьбы p, высоту гайки H, наружный диаметр опорной поверхности гайки D 1, диаметр отверстия под болт d 0. Результаты занести в табл. 2.1 отчета. 3. Внутренний диаметр резьбы d 1, средний диаметр d 2и внутренний диаметр болта по дну впадины d 3принять по табл. 1.1 лабораторной работы № 1. 4. Вычислить допустимую силу затяжки болта [ F зат]по формуле (2.7). 5. Вычислить значения этой силы:
и записать их в табл. 2.2 и 2.3 отчета. 6. Задать предварительный натяг индикатора в 1,5...2 оборота и установить его большую стрелку на нулевое деление. 7. Установить болт в прибор, завернуть гайку от руки до устранения осевого люфта, что контролируется по стрелке индикатора 8 (см. рис. 2.1) на установке.
Примечание. В результате тарировки динамометрической пружины и торсионного динамометрического ключа установлены следующие тарировочные коэффициенты:
Таким образом, сила затяжки
8. Определить число делений n 1индикатора 8 (см. рис. 2.1) по значениям силы затяжки и тарировочному коэффициенту μ1. Результаты записать в табл. 2.2 отчета. 9. Затянуть болт динамометрическим ключом последовательно до четырех значений силы затяжки. Записать числа делений индикатора торсионного ключа в табл. 2.2 отчета. 10. Определить величину 11. По полученным данным построить график зависимости силы затяжки F затот момента завинчивания T зав. 12. По формуле (2.3) для каждого значения силы затяжки и момента завинчивания 13. Вычислить приведенный коэффициент трения f 1по формуле (2.3) и коэффициент трения в резьбе f pпо формуле (2.4). Результаты записать в табл. 2.2 отчета. 14. Вычислить среднее значение давления p рна витках резьбы по уравнению (2.8) и записать в табл. 2.2 отчета. 15. По полученным данным построить график зависимости коэффициента трения в резьбе f pот удельного давления p р. 16. При испытании со специальной втулкой вычислить момент трения на торце гайки по уравнению
Значения Т рполучены в предыдущем опыте. 17. По формуле (2.6) вычислить значения коэффициента трения f тна торце гайки и записать в табл. 2.3 отчета. 18. По формуле (2.9) вычислить давление на торце гайки p т. Результаты занести в табл. 2.3 отчета. 19. Построить график зависимости коэффициента трения на торце гайки от давления Образец оформления отчета
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Лабораторная работа № 2
Определение коэффициента трения,
Цель работы: 1. Определение коэффициента трения в резьбе. 2. Построение графика зависимости f pот удельного давления на витках резьбы P р. 3. Определение коэффициента трения на торце гайки f т. 4. Построение графика зависимости f тот удельного давлен
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.16.251 (0.017 с.) |


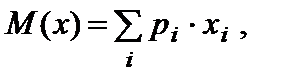 (1)
(1)








 .
.


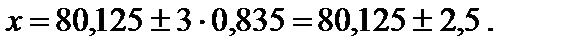

 м (деление).
м (деление).

 Н
Н  , где
, где

 Н
Н 
 (1.1)
(1.1) ,
,  .
. .
.
 (1.2)
(1.2) , (1.3)
, (1.3)
 − постоянная величина для заданных условий опыта. Таким образом, Fr = f(T зав ) является линейной зависимостью.
− постоянная величина для заданных условий опыта. Таким образом, Fr = f(T зав ) является линейной зависимостью. . (1.4)
. (1.4) МПа.
МПа. Н.
Н. , (1.4)
, (1.4) − тарировочный коэффициент, получаемый при деформировании пружины на силоизмерительной машине;
− тарировочный коэффициент, получаемый при деформировании пружины на силоизмерительной машине;
 .
. .
. по теоретическим и экспериментальным данным.
по теоретическим и экспериментальным данным.



 .
. .
.
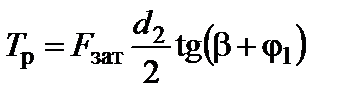 . (2.1)
. (2.1) где p − шаг резьбы, мм.
где p − шаг резьбы, мм. . (2.2)
. (2.2) . (2.3)
. (2.3) и действительный коэффициент трения в резьбе
и действительный коэффициент трения в резьбе  связаны зависимостью
связаны зависимостью .
. . Поэтому коэффициент трения в резьбе
. Поэтому коэффициент трения в резьбе . (2.4)
. (2.4) . (2.5)
. (2.5)
 . (2.6)
. (2.6)
 (2.7)
(2.7) МПа.
МПа. (2.8)
(2.8) . (2.9)
. (2.9)
 ;
;  ;
; 
 для динамометрической пружины;
для динамометрической пружины; для динамометрического ключа.
для динамометрического ключа. , Н, и момент на динамометрическом ключе
, Н, и момент на динамометрическом ключе  , Н·мм. Здесь n 1 и n 2 – соответственно числа делений индикаторов 8 (см. рис. 2.1) и динамометрического ключа.
, Н·мм. Здесь n 1 и n 2 – соответственно числа делений индикаторов 8 (см. рис. 2.1) и динамометрического ключа. вычислить приведенный угол трения в резьбе φ1 и записать в табл. 2.2 отчета.
вычислить приведенный угол трения в резьбе φ1 и записать в табл. 2.2 отчета. .
. .
.


