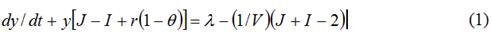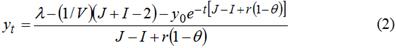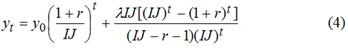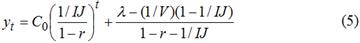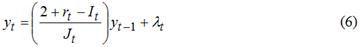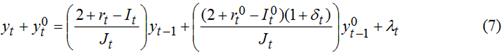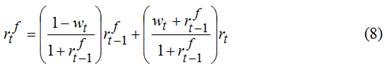Методические подходы к прогнозированию динамики государственного долга (может, когда-нибудь пригодится)

Не относится к числу названных моделей так называемая RMSM-X-модель, разработанная в Мировом банке и позволяющая прогнозировать как потребности страны во внешних заимствованиях, так и способность осуществлять платежи по их обслуживанию. Это связано с тем, что данная модель строится по принципу межотраслевого баланса, а, следовательно, является довольно громоздкой и ее использование происходит в основном в режиме «черного ящика», когда даже приблизительно нельзя предсказать, что будет на выходе. Таким образом, ниже мы ограничимся рассмотрением только наиболее простых, но в тоже время, как нам кажется, наиболее эффективных подходов.

Модель Л.Е.Соколовского. Одной из первых зрелых попыток формализации долговой динамики явилась модель, предложенная в 1991 г. Л.Е.Соколовским [1]. Все построения Л.Е.Соколовского в конечном счете сводились к весьма простой и элегантной дифференциальной модели движения доли внутреннего долга в национальном продукте. Итоговое дифференциальное уравнение выглядело следующим образом:

где использованы следующие обозначения: индекс цен (инфляции) I_t=P_t/P_t-1; индекс реального роста производства J_t=X_t/X_t-1; относительный внутренний долг y_t=B_t/Q_t; P_t – средний уровень цен; X_t – объем выпуска в натуральном выражении; Q_t=P_tX_t – номинальный валовой внутренний продукт (ВВП); D_t=G_t–T_t – абсолютный первичный дефицит государственного бюджета; G_t – государственные расходы (исключая расходы по обслуживанию государственного долга); T_t – государственные доходы; относительный первичный дефицит бюджета λ_t=g_t–θ_t; средняя ставка налогообложения θ_t=T_t/Q_t; доля государственных расходов в валовом внутреннем продукте g_t=G_t/Q_t; B_t – объем внутреннего долга; r_t – средняя номинальная процентная ставка по долговым обязательствам государства; V_t=Q_t/M_t – скорость обращения денег; M_t – величина денежной массы; t – период времени (в нашем случае – год).

Решением модели (1) является следующая экспоненциальная функция:

Какие можно отметить «плюсы» и «минусы» данной модели?

К числу «минусов» можно отнести то, что модель описывает динамику только внутреннего долга, но не рассматривает внешний долг. Совершенно очевидно, что для внешнего долга должна быть построена похожая модель, но ее окончательного вида в работе Л.Е.Соколовского нет.

К числу «плюсов» следует отнести тот факт, что построенная модель учитывает общий механизм покрытия бюджетного дефицита за счет денежно-кредитной эмиссии и за счет осуществления новых заимствований. В модели Л.Е.Соколовского этот принцип описывается следующим простым уравнением:

Таким образом, в модели фигурирует монетарный фактор, что имеет большое значение и, несмотря на это, отсутствовало в более поздних разработках. Однако сам учет монетарного фактора проводился автором не совсем корректно. Дело в том, что величина искомой денежно-кредитной эмиссии отождествлялась с абсолютным приростом денежной массы (агрегата М2). Такой подход является неправомерным.

Модель О.О.Замкова. Следующим этапом в построении прогнозно-аналитического инструментария долговой сферы явилась модельная схема О.О.Замкова, предложенная в 1997 г. [3]. Методологически О.О.Замков шел несколько иным путем, чем Л.Е.Соколовский, хотя в целом определенная преемственность между их разработками имела место. В работе [3] были получены компактные и очень удобные зависимости, которые можно использовать как для анализа, так и для прогнозирования долговых тенденций.

Основная зависимость, полученная О.О.Замковым, имела следующий вид (в ранее использованных нами обозначениях):

Здесь, как и в предыдущей модели, относительный показатель внутреннего долга увязан с первичным дефицитом бюджета, процентом по долговым обязательствам, темпами экономического роста и инфляцией. Однако при всей своей строгости и практичности данная модель также имеет ряд недостатков.

Во-первых, это ограничение долговой проблематики вопросами только внутреннего долга; внешний долг в ней как таковой не учитывается. Здесь также просматривается возможность расширить модель и на внешнедолговой сегмент, однако для этого надо перестраивать всю исходную модельную схему О.О.Замкова.

Во-вторых, в модели отсутствует монетарный фактор. Так, например, при выведении своих зависимостей автор исходит из того, что государственный внутренний долг равен накопленной сумме бюджетных дефицитов за соответствующие годы [3, с.8]. Грубо говоря, так оно и есть. Однако при моделировании данного процесса нельзя не учитывать и тот факт, что сам бюджетный дефицит погашается не только за счет займов, но и за счет денежно-кредитной эмиссии. «Потеря» монетарного (эмиссионного) фактора в схеме О.О.Замкова делает ее, с одной стороны, менее корректной с теоретической точки зрения, а с другой – менее приспособленной к практическим расчетам. Действительно, при обращении к реальным цифрам формула (4) будет давать систематические погрешности из-за недоучета фактора денежной эмиссии. Фактически модель (4) описывает частный случай, когда государство все бюджетные проблемы решает только с помощью долговых инструментов без привлечения монетарных средств. Такой подход может применяться, например, при наблюдающемся устойчивом профиците бюджета, когда использование эмиссионного механизма неэффективно и избыток бюджетных средств тратится на погашение имеющегося долга. В общем же случае модель О.О.Замкова при всей ее плодотворности все же можно квалифицировать как определенный шаг назад по сравнению с моделью Л.Е.Соколовского. Кстати говоря, различие в методологических подходах к моделированию динамики долга во многом объясняет довольно сильное различие формул (2) и (4).

Таким образом, помимо включения в ее состав фактора внешнего долга, модель О.О.Замкова нуждается и в расширении набора объясняющих факторов, а именно, в учете монетарно-эмиссионных механизмов.

Модель Е.В.Балацкого. Следующим шагом в направлении моделирования долговой динамики была модель, предложенная в 1997 г. Е.В.Балацким [4]. Принципы, которые были положены в основу этой модели, были те же, что и в модели Л.Е.Соколовского, со всеми вытекающими отсюда недостатками. Различие состояло в добавлении одного уравнения накопления долга, которое в модели Л.Е.Соколовского в явной форме отсутствовало, и в переходе от дифференциальной схемы анализа к разностной.

Итоговое соотношение для динамики относительного внутреннего долга имело следующий вид:

Несложно видеть, что формулы (2), (4) и (5) немного похожи между собой и в тоже время различны. Уже сам по себе этот факт со всей очевидностью обнажает проблему выбора конкретной схемы расчета, так как все приведенные формулы дают разные количественные результаты и базируются на неодинаковых принципах описания долгового процесса.

В работе [4] была также предпринята одна из первых попыток объединения внутреннего и внешнего долга в рамках единой аналитической схемы. Здесь использовался следующий методологический прием. Вся модель описывалась несколькими уравнениями. Первое из них отражало формирование общего бюджетного дефицита, который задавался в виде суммы первичного дефицита, процентов, начисляемых по внутреннему долгу, и процентов, начисляемых по внешнему долгу и оцениваемых в национальных денежных единицах с помощью текущего валютного курса. Второе уравнение описывало процесс покрытия бюджетного дефицита за счет денежной эмиссии, прироста внутреннего и внешнего долга. Наконец, динамика каждого вида долга описывалась «своим» разностным уравнением. В дальнейшем все уравнения редуцировались в одно, для чего использовалась гипотеза о неизменности структуры долга в национальной валюте [4, с.48]. Сама редукция проводилась в целях получения максимально аналитичной зависимости, позволяющей проигрывать различные варианты структурно-долговой политики, то есть политики по предпочтению того или иного вида долгового инструмента.

Идеология такого «совместного» рассмотрения внешнего и внутреннего долгов базировалась на гипотезе об их взаимозаменяемости. Надо сказать, что такая гипотеза справедлива именно к российским условиям, где используется «валютный» критерий разделения государственного долга на внешний и внутренний. В общем случае, когда классификация долгов происходит в соответствии с «резидентным» критерием, принятая гипотеза справедлива лишь отчасти. Кроме того, при анализе долговых стратегий страны совершенно неправомерно автономно анализировать динамику внешнего и внутреннего долга; значительно логичней проводить одновременный анализ обеих сторон долговой политики государства.

Однако предложенный подход имел ряд недостатков. Во-первых, получившиеся зависимости оказались довольно сложными и громоздкими, что снижало их прикладную ценность. Во-вторых, как и в модели Л.Е.Соколовского, в модели Е.В.Балацкого неверно учитывался монетарный фактор. И, в-третьих, в уравнении, описывающем покрытие бюджетного дефицита, была допущена неточность, а именно: в нем присутствовал компонент, учитывающий рост стоимости прошлогоднего внешнего долга из-за изменения валютного курса. Данный компонент в подобном уравнении является лишним и своим присутствием искажает весь последующий анализ.

Таким образом, модель Е.В.Балацкого, позволяя рассматривать совокупный долг страны, нуждается в серьезной инструментальной корректировке и упрощении.

Модель Вавилова-Трофимова. Следующим этапом в развитии прогнозного инструментария долгового процесса явилась модель, предложенная в 1997 г. А.П.Вавиловым и Г.Ю.Трофимовым в [5]. В отличие от предыдущих авторов А.П.Вавилов и Г.Ю.Трофимов не стремились к созданию максимально аналитичной схемы формирования государственного долга, а изначально преследовали сугубо прикладную цель – построить модель, пригодную для прогнозирования долговой ситуации с учетом возможных нестационарных траекторий ключевых макроэкономических параметров. Для государственного долга без учета его валютной структуры их модель записывалась в виде следующего рекуррентного соотношения (с учетом ранее принятых обозначений):

где r_t*=r_t-(I_t-1) - усредненный реальный процент по долговым обязательствам (за вычетом из номинального процента темпа инфляции).

Основной гипотезой, положенной в основу модели (6), является предположение о неиспользовании государством инфляционного налога для финансирования своих расходов [5]. Таким образом, в данной схеме также изначально не учитывается монетарный фактор, что несколько упрощает и обедняет предложенную модель. Применительно к случаю, учитывающему отдельно внутренний и внешний долг, уравнение (6) модифицируется к следующему виду:

где r⁰ – номинальный процент за рубежом (средняя ставка внешнему долгу); I⁰ – индекс инфляции за рубежом (в США); δ - темп прироста реального курса доллара, определяемый как 1 + δ_t = I_t⁰k_t / I_tk_t-1; k_t – номинальный курс доллара в течение периода t.

Модель (7) явилась первой моделью, которая достаточно просто и аккуратно описывает совместную динамику как внутреннего, так и внешнего долга. Однако в ней есть определенная специфика, на которой стоит специально остановиться.

Дело в том, что модель Вавилова-Трофимова оперирует суммой внутреннего и внешнего долга, в то время как, например, в схеме Е.В.Балацкого каждый вид долга описывается своим собственным уравнением. Переход к такой редуцированной модели предполагает рассмотрение единого долгового потока, который нельзя «разложить» на две части, так как его валютная структура может меняться волюнтарным путем в различных направлениях. Фактически это означает неявное использование постулата о неограниченной взаимозамещаемости внутреннего и внешнего долгов. Методически этот факт проявляется в свободе формирования текущих долей внутреннего и внешнего долгов в ВВП, исходя лишь из общей суммы долгового бремени предыдущего периода и текущей величины первичного бюджетного дефицита. Такой подход следует признать совершенно справедливым и прогрессивным с точки зрения моделирования, хотя очевидно и то, что диапазон варьирования структуры государственного долга в реальности не слишком уж велик. Тем не менее, подобный поход вполне оправдан и, главное, позволяет проигрывать сценарии по выбору оптимального сочетания внутренних и внешних долгов. Тем более, что главное в подобных расчетах – понять будущие масштабы совокупного долгового бремени, ибо, как это предполагается в модели Вавилова-Трофимова, оба вида долга равнотяжелы и априори отдать предпочтение какому-либо из них нельзя.

И все же основным недостатком модели Вавилова-Трофимова, на наш взгляд, является отсутствие монетарного фактора. Как справедливо отмечают сами авторы, в 1995 г. в России на смену денежной экспансии пришла экспансия внутреннего долга [5]. Для описания последней построенная ими модель вполне пригодна, но для описания чистой денежной экспансии или смешанных стратегий, которые часто имеют место на практике, такая модель совершенно не приспособлена. Именно в этом направлении и необходимо совершенствование модели Вавилова-Трофимова.

Модель А.Кнастера. Следующей вехой в развитии модельного инструментария для прогнозирования государственного долга явилась модель А.Кнастера, предложенная в 1998 г. в работе [6]. Построенная модель предполагала несколько инноваций.

Во-первых, в расчетную схему введено понятие амортизации государственного (внутреннего и внешнего) долга. Действительно, определенная часть «старых» долгов в плановом порядке должна погашаться в соответствии с нормой амортизации долга w=1/τ, где τ – средний срок заимствований. Амортизация прошлых долговых обязательств в совокупности с процентными платежами по ним образует сумму расходов по обслуживанию долга. При всей очевидности данного элемента долгового процесса он отсутствовал во всех ранее перечисленных модельных схемах. Таким образом, все предыдущие четыре подхода либо заведомо занижают долговые платежи, либо вообще их не рассматривают. На наш взгляд, данное «ноу-хау» модели А.Кнастера обязательно должно быть использовано при разработке более совершенного инструментария, особенно, если учесть, что его введение в расчетную схему практически никак ее не усложняет.

Во-вторых, в модели А.Кнастера проводится различие между переменными и фиксированными ставками по долгу. Действительно, в настоящее время действуют как фиксированные процентные ставки, установленные на определенном уровне при заключении договора о займе, так и переменные, исчисляемые путем прибавления фиксированной маржи (спрэда) к заранее выбранной базовой ставке, «плавающей» в зависимости от рыночной конъюнктуры [6, с.65]. В качестве базовой ставки часто используется ставка ЛИБОР (средняя ставка процента по краткосрочным межбанковским депозитам на евровалютном рынке в Лондоне). Так, например, долг бывшего СССР перед Лондонским клубом должен обслуживаться Россией по ставке (29/16)ЛИБОР (но не более 8%) [6, с.65]. Переменные и фиксированные процентные ставки по-разному влияют на динамику усредненной ставки процента. В связи с этим в модели А.Кнастера фигурирует рекуррентное уравнение для пересчета фиксированных усредненных ставок r_t^ƒ [6, с.73]:

Как справедливо отмечает А.Кнастер, влияние ставок новых займов на величину усредненной ставки будет нарастать по мере погашения старых займов [6, с.66]. Хотя, на наш взгляд, в агрегированных расчетах такими тонкими эффектами можно пренебречь, само включение их в модельную схему представляется достаточно плодотворным.

В-третьих, модель А.Кнастера учитывает фактор дифференциации заимствований по их продолжительности. При этом автор предлагает различать краткосрочные (менее 1 года), средне- и долгосрочные (более 1 года) займы. Этот момент представляется достаточно важным, так как позволяет оценить влияние на динамику государственного долга возможных сдвигов во временной структуре государственного долга. Таким способом можно фактически напрямую учесть фактор дюрации, который в подавляющем большинстве прогнозно-аналитических схем не учитывается.

В-четвертых, сама идеология моделирования в анализируемой прогнозной схеме иная, нежели в предыдущих схемах. Так, А.Кнастер использует три типа уравнений: платежей, новых заимствований и накопления долга. При этом данные уравнения записываются отдельно для внутреннего и внешнего долга, каждый из которых предполагает три разновидности: кратко-, средне- и долгосрочные займы.

Однако предложенная А.Кнастером модель имеет и ряд очевидных недостатков. Это, во-первых, абстрагирование от монетарного фактора. По сути дела это означает, что в предложенной модели учет довольно тонких аспектов долговой политики проводится на фоне грубого игнорирования «тяжелых» факторов, лежащих на поверхности явления. Это уже само по себе делает рассмотренную схему методологически несбалансированной. Во-вторых, внешние и внутренние долги фигурируют в модели сами по себе и никак не связаны, хотя по определению ясно, что они находятся в состоянии взаимовлияния. Кроме того, в окончательных зависимостях выпадает параметр бюджетного дефицита, что сильно подрывает прогностические возможности модели. И, в-третьих, сама модель оказывается довольно громоздкой на фоне отсутствия важных макроэкономических параметров.

Рассмотренные выше модели позволяют глубже понять проблемы, возникающие при моделировании долговой динамики и более взвешенно относиться к любым прогнозам в данной сфере. Главным же результатом проведенного анализа является возможность сформулировать три принципа, которых необходимо придерживаться при совершенствовании схемы прогнозирования внешнего долга.

Во-первых, изучение долговой проблематики не должно ограничиваться анализом динамики накопленного государственного долга, но должно также включать рассмотрение траекторий расходов по его обслуживанию. Во-вторых, изучение динамики внешнего долга должно проводиться в рамках более общей проблемы – проблемы совокупного государственного долга. Этот принцип предполагает совместный анализ динамики внешнего и внутреннего долга страны. В-третьих, модельные построения должны учитывать монетарный фактор, так как денежная эмиссия является серьезным «заменителем» долговых инструментов.