
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Технічні характеристики авіаційних гіперспектральних системСодержание книги
Поиск на нашем сайте
Технічні характеристики авіаційних гіперспектральних систем Носій Бортова гіперспектральна апаратура Висота польоту км Кількість спектральних каналів Спектральний діапазон, мкм Кутова розрізненість, мрад Кут поперечного огляду ER-2A AVIRIS (Airborne Visible/ Infrared Imaging Spectrometer) 2.5-21 0.4-2.45 1.0 WC-135U AIS-2 (Airborne Imaging Spectrometer) 3-12 0.8-2.4 1.33 3.5 PC-6 AHS-75 (Airborne Hyperspectral Scanner) 1-5 0.45-2.5 2.5 Do-228 DAIS-7915 (Digital Airborne Imaging Spectrometer) 0.5-10 0.4-12.0 3.3 Do-228 ROSIS (Reflective Optics System Imaging Spectrometer) 0.5-10 0.43-0.85 0.56 LearJet 23 CASI-1500 (Compact Airborne Spectrographic Imager) 0.5-10 0.43-0.87 0.45 40.5 LearJet 23 SASI-640 (Shortwave Infrared Airborne Spectrographic Imager) 0.5-10 0.95-2.45 1.1 40.5 CV-580 HYDICE (Hyperspectral Digital Imagery Collection Experiment) 1.5-8 0.4-2.5 0.53 40,5 WB-57F HyMap+ (Hyperspectral Mapper Plus) 2-10 0.4-2.5 2.0 61.3 WB-57F HySpex-1600 (Airborne Hyperspectral Imaging System) 2-10 0.4-1.0 0.375 61.3 WB-57F MAIS (Modular Airborne Imaging Spectrometer) 2-10 0.44-11.8 3.0 WB-57F OMIS-II (Operational Modular Imaging Spectrometer) 2-10 0.4-5.0 1.5 WB-57F MIVIS (Multispectral Infrared and Visible Imaging Spectrometer) 2-10 0.43-12.7 2.0 OP-3C PHILLS (Pushbroom Hyperspectral Imager for Low- Light Spectroscopy) 0.1-6 0.4-1.0 5.2
1.5. Передавальні властивості гіперспектральних аерокосмічних зображень Тракт походження гіперспектрального оптичного сигналу, починаючи від об’єкта випромінювання, середовища між об’єктом та іконічною системою аж до перетворення на зображення, складається з окремих послідовно з’єднаних оптичних передавальних ланок. Гіперспектральна система перетворює просторовий розподіл оптичного випромінювання в площині об’єкта Передавальні властивості ланки описуються сигналом на її виході під час подавання деякого стандартного сигналу спеціального вигляду на вхід. Найчастіше використовують імпульсну передавальну функцію g(x) – реакцію системи на одиничний вхідний імпульс – δ-функцію δ(х), причому
(1.1) Під час аналізу іконічних систем g(x) називається функцією розсіювання точки (ФРТ) і описує розподіл оптичного сигналу в зображенні ідеальної точки, утвореного іконічною системою. Повний оптичний сигнал в зображенні визначається імпульсною функцією через інтеграл-згортку: Якщо оптичні сигнали Е(х) описані їх просторово-частотними спектрами Е(N), де N – просторова частота, то передавальні властивості іконічної системи характеризуються їхньою оптичною передавальною функцією (ОПФ). Оптична передавальна функція П(N) визначається як відношення комплексного просторово-частотного спектра сигналу на виході Е(N) системи до комплексного просторово-частотного спектра Оскільки розподіл оптичного сигналу в зображенні описується інтервалом – згорткою (1.2), то між оптичною передавальною функцією П(N) та функцією розсіювання точки g(x) існує однозначний взаємозв’язок: ОПФ і ФРТ можна отримати одну з одної прямим та оберненим перетворенням Фур’є: З (1.4) випливає, що просторово-частотний спектр зображення (1.3) визначається як добуток просторово-частотного спектра вхідного оптичного сигналу що істотно полегшує аналіз іконічної системи загалом. Гіперспектральна іконічна система, на відміну від звичайної, формує оптичний сигнал, який поширюється не тільки у просторовому, а й додатково в спектральному вимірі. Тому Фур’є – перетворення (1.3) в гіперспектральній системі стає багатовимірним і дуже важко піддається аналітичному розв’язку. Крім того, застосування багатовимірного перетворення Фур’є не описує передавальні властивості системи зрозумілим універсальним методом, а просто переводить багатовимірний опис у просторово-частотну область. Для звичайних (одновимірних) іконічних систем таким універсальним показником є функція передавання модуляції (ФПМ) – дійсний модуль комплексної ОПФ. Ця характеристика повність описує передавальні властивості іконічної системи, має об’єктивний характер вимірювань та ґрунтується на добре опрацьованому математичному апараті. Зазначимо, що оцінювання іконічної системи за ФПМ охоплює оцінку за розрізнювальною здатністю, тому що остання визначається точкою за ФПМ.
Окреме оцінювання ФПМ окремих спектральних каналів гіперспектральної системи є неефективним, оскільки не враховує взаємних зв’язків між зображеннями в каналах. Для визначення просторової розрізненності іконічної системи, крім її ФПМ, додатково потрібна модель шумів, яка виражається функцією межового контрасту. Причому визначення моделі шумів пов’язане з тими самими труднощами, що й визначення ФПМ. Впровадження іконічних систем із дискретними багатоелементними фотоприймачами призводить до специфічних ефектів відтворення саме цифрових аерокосмічних знімків, що пов’язано з пастеризацією зображень. Особливо вказані ефекти заважають експериментальному визначенню ФПМ за цифровими аерокосмічними знімками. Загальною рисою всіх труднощів є статистичний характер процесів, що відбуваються в іконічній системі. Подолати ці труднощі повністю або частково можна, якщо повернутися до первинної мети оцінювання просторової розрізненості іконічних систем, саме – до виявлення об’єктів за знімками. Необхідно визначити, що сам феномен розмиття зображення ідеальної точки в реальній іконічній системи тісно пов'язаний з оптичними абераціями, девіаціями реєстрування фотонів напівпровідниковими фотоприймачами та передавання фотоелектронів мікроелектронними трактами, тобто є квантово-механічними, а значить, принципово імовірнісними ефектами. В цьому контексті ФРТ можна розглядати як розподіл квантів у фізичній точці зображення, причому їх кількість швидко зменшується від центра до країв. Якщо вважати початкову кількість квантів фіксованою та достатньо великою, ФРТ набуває сенсу щільності просторового розподілу імовірності оптичного сигналу в вихідному зображенні іконічної системи Де З цього міркування випливає суто імовірнісний характер виявлення об’єктів на аерокосмічних знімках, який практично не враховується класичним апаратом просторово-частотного аналізу, розмиває поняття просторової розрізненості та змушує дослідників додатково залучати інші імовірнісні моделі виявлення об’єктів на зображеннях, подібні до формули Живичина. Сьогодні використання статистичних методів обробки цифрових аерокосмічних зображень для оцінювання їх передавальних властивостей є доволі перспективним, але більшість відомих підходів пов’язані з розділенням радіометричних полів, тобто не є уніфікованими. Разом з тим, бажано не втратити цінних напрацювань, отриманих під час просторово-частотного аналізу аналогових іконічних систем. Для одновимірних панхроматичних зображень використовують імовірне перетворення, яке визначає для кожної точки зображення імовірність безпомилкового розділення верхнього та нижнього б’єфів (помилок) перехідної характеристики, що відображає ідеальний детермінований стрибок сигналу між сегментами вздовж вибраного напрямку. Імовірнісне перетворення в неявній формі враховує вплив на якість зображення привнесених шумів. Воно легко узагальнюється на багатовимірні гіперспектральні знімки за допомогою оцінювання імовірності за багатовимірними розподілами щільності імовірності.
Нехай на гіперспектральному аерокосмічному зображенні за допомогою імовірнісного перетворення або іншим способом виділено багатовимірну перехідну характеристику вздовж визначеного напрямку. Якщо вздовж цього напрямку обчислити розподіл імовірності Р(х) будь-якого з б’єфів багатовимірної перехідної характеристики вздовж вісі х, одержимо одновимірну імовірнісну перехідну характеристику. Просторова похідна цієї функції Повертаючись до фізичного сенсу, з відомими припущеннями можна вважати одержану функцію Отже, просторово-статистичний підхід дає змогу згорнути багатовимірну ФРТ гіперспектральної іконічної системи до еквівалентної одновимірної без втрати інформативності та наочності одержуваних оцінок. Подальше застосування перетворення Фур’є до еквівалентної ФРТ дає змогу обчислити еквівалентну комплексну ОПФ гіперспектральної системи, дійсний модуль якої є еквівалентною ФПМ – основним показником передавальних властивостей гіперспектральних аерокосмічних зображень. Одержання еквівалентних ФПМ дає змогу повніше та теоретично обгрунтованіше оцінювати передавальні властивості гіперспектральних аерокосмічних зображень для забезпечення відповідності чинним міжнародним стандартам просторово-частотного аналізу.
|
|||||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.233 (0.008 с.) |

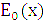 на розподіл у площині зображення Е(х).
на розподіл у площині зображення Е(х).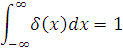
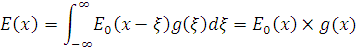 (1.2)
(1.2)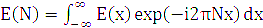 , (1.3)
, (1.3)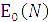 сигналу на виході:
сигналу на виході: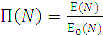 . (1.4)
. (1.4)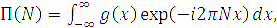 (1.5)
(1.5)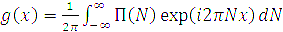 . (1.6)
. (1.6)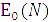 та оптичної передавальної функції системи П(N). При послідовному з’єднанні декількох передавальних ланок їх спільна ОПФ визначається співвідношенням
та оптичної передавальної функції системи П(N). При послідовному з’єднанні декількох передавальних ланок їх спільна ОПФ визначається співвідношенням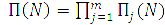 , (1.7)
, (1.7)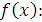
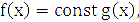 (1.8)
(1.8)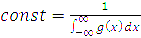 – нормувальний множник, який за формулою (1.1) дорівнює 1, якщо знехтувати втратами енергії сигналу або підсиленням.
– нормувальний множник, який за формулою (1.1) дорівнює 1, якщо знехтувати втратами енергії сигналу або підсиленням.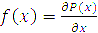 є щільністю розподілу імовірності в точці гіперспектрального зображення.
є щільністю розподілу імовірності в точці гіперспектрального зображення.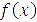 статисттичним описом еквівалентної ФРТ гіперспектрального аерокосмічного знімання, причому еквівалентність забезпечується саме з погляду прикінцевої мети оцінювання – виявлення об’єктів на зображенні.
статисттичним описом еквівалентної ФРТ гіперспектрального аерокосмічного знімання, причому еквівалентність забезпечується саме з погляду прикінцевої мети оцінювання – виявлення об’єктів на зображенні.


