
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Событие, которое может произойти или не произойти при проведении опытаСодержание книги
Поиск на нашем сайте !!!!! Перепишите таблицу! По элементам теории вероятностей также целесообразно иметь опорный конспект: Основные понятия понятие определение вероятность Случайное событие Событие, которое может произойти или не произойти при проведении опыта 0 ≤ Р (А) ≤ 1 Достоверное событие Событие, которое происходит при проведении опыта всегда Р(А) = 1 Невозможное событие Событие, которое не может произойти ни при каком исходе опыта Р(А) = 0 Равновозможные событие События, которые имеют равные возможности произойти 0 ≤ Р (А) ≤ 1 Противоположными событие События А и В называются противоположными, если всякое наступление события А означает ненаступление события В, а ненаступление события А – наступление события В. Р(А) = 1- Р(В) Нахождение вероятности Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти: число N всех возможных исходов данного испытания; количество N(A) тех исходов, в которых наступает событие А; частное оно и будет равно вероятности события А. Р(А) =
Решение задач. Про решайте устно! Примеры.
Решение. Число стандартных подшипников равно 1000 – 30 = 970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из N = 1000 равновероятных исходов, из которых событию А благоприятствуют N(A) = 970 исходов. Поэтому Ответ: 0,97. 2. Найдем вероятность того, что при одном бросании игральной кости (кубика) выпадает: а) три очка; б) число очков, кратное трем; в) число очков больше трех; г) число очков, не кратное трем. Решение. Всего имеется N=6 возможных исходов: выпадение 1,2,3,4,5,6 очков. Считаем, что эти исходы равновозможны. а) Только при одном из исходов N(А)=1 происходит интересующее нас событие А – выпадение трех очков. Вероятность этого события б) При двух исходах N(B) = 2 происходит событие B: выпадение числа очков кратных трем: выпадение или трех или шести очков. Вероятность такого события в) При трех исходах N(C) = 3 происходит событие C: выпадение числа очков больше трех: выпадение четырех, пяти или шести очков. Вероятность этого события г) Из шести возможных выпавших чисел четыре (1, 2, 4 и 5) не кратны трем, а остальные два (3 и 6) делятся на три. Значит, интересующее нас событие D, наступает в четырех случаях, т.е. N(D) = 4. Вероятность такого события: Ответ: а)
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 12; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.99.115 (0.009 с.) |

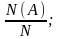
 Р(А) =
Р(А) = 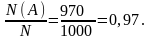
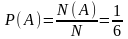 .
.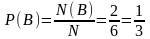 .
.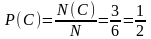 .
.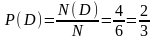 .
.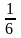 ; б)
; б) 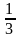 ; в)
; в) 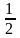 ; г)
; г) 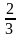 .
.


