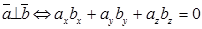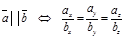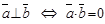Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства скалярного произведенияСодержание книги
Поиск на нашем сайте Обрати внимание! 3. Если угол между векторами прямой, то скалярное произведение векторов равно нулю, так как косинус прямого угла равен 0. Обратное суждение: если скалярное произведение векторов равно нулю, то эти векторы перпендикулярны. Вектор, умноженный на самого себя, будет числом, которое называется скалярным квадратом вектора. Скалярный квадрат вектора равен квадрату длины данного вектора и обозначается как 2. Свойства скалярного произведения 1. Скалярное произведение обладает переместительным свойством:
2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: 3. Скалярное произведение обладает распределительным свойством:
4. Скалярный квадрат вектора равен квадрату его длины:
В частности: вектор 5. Если векторы Так как Выражение скалярного произведения через координаты Пусть заданы два вектора
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат. Пример 1. Доказать, что диагонали четырехугольника, заданного координатами вершин Решение: Составим вектора
Отсюда следует, что Угол между векторами. Определение угла Отсюда следует условие перпендикулярности ненулевых векторов
Два вектора называются коллинеарными, если выполняется: Свойство: Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. Использование скалярного произведения
|
||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 42; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

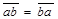 .
.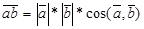 , а
, а 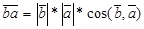 , И так как
, И так как 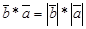 , как произведение чисел
, как произведение чисел 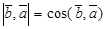 ,
, 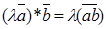
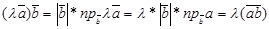
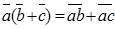
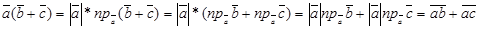 .
.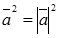
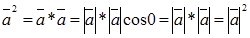
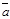 возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль
возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль 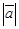 , т.е.
, т.е. 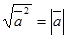 (
( 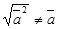 ).
). (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если
(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если 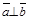 , то
, то 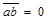 . Справедливо и обратное утверждение: если
. Справедливо и обратное утверждение: если 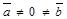 , то
, то 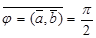 ,
, 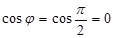 . Следовательно,
. Следовательно, 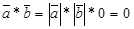 . Если же
. Если же 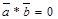 и
и 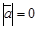 , то
, то 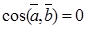 . Отсюда
. Отсюда 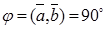 , т.е.
, т.е. 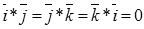 .
.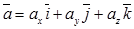 и
и 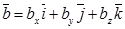 .
.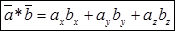
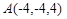 ,
, 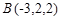 ,
, 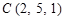 ,
, 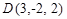 , взаимно перпендикулярны.
, взаимно перпендикулярны.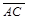 и
и 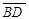 , лежащие на диагоналях данного четырехугольника. Имеем:
, лежащие на диагоналях данного четырехугольника. Имеем: 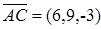 и
и 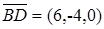 . Найдем скалярное произведение этих векторов:
. Найдем скалярное произведение этих векторов: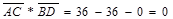 .
.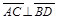 . Диагонали четырехугольника
. Диагонали четырехугольника 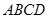 взаимно перпендикулярны.
взаимно перпендикулярны.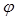 между ненулевыми векторами
между ненулевыми векторами 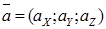 и
и 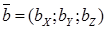
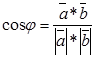 , т.е.
, т.е. 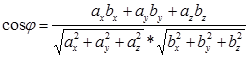
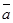 и
и