Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV. Формирование умений и навыков.Содержание книги
Поиск на нашем сайте
Рассматриваем задачи на применение формулы нахождения числа сочетаний из п по k. Для предотвращения формального применения формулы требуем обоснования ее выбора. Упражнения: № 768. Р е ш е н и е Выбираем 2 учащихся из 7, порядок выбора не имеет значения (оба выбранных пойдут на олимпиаду как полностью равноправные); количество способов выбора равно числу сочетаний из 7 по 2:
О т в е т: 21 способ. № 770. Р е ш е н и е Выбор 6 из 10 без учета порядка:
О т в е т: 210 способов. № 772. Р е ш е н и е Из 11 человек 5 должны поехать в командировку: а) Заведующий едет, нужно выбрать еще 4 из 10 оставшихся:
б) Заведующий остается, нужно выбрать 5 из 10 сотрудников:
О т в е т: а) 210 способов; б) 252 способа. Следующие три задачи – повышенной сложности. № 773. Р е ш е н и е а) Словарь выбирается, нужно выбрать еще 2 книги из 11:
б) Словарь не выбирается, выбираем 3 книги из 11:
О т в е т: а) 55 способов; б) 165 способов. № 774. При решении используется не только формула числа сочетаний, но и комбинаторное правило умножения. Р е ш е н и е Сперва выбираем 4 маляров из 12:
Затем выбираем 2 плотников из 5:
Каждый из способов выбора маляров можно скомбинировать с каждым выбором плотников, следовательно, всего способов (по комбинаторному правилу умножения): 495 · 10 = 4950. О т в е т: 4950 способов. № 775. Р е ш е н и е Нужно сделать два выбора: 3 книги из 10 (
О т в е т: 720 способов. V. Итоги урока. В о п р о с ы у ч а щ и м с я: – Что называется сочетанием из п элементов по k? – Запишите формулу вычисления числа сочетаний из п элементов по k. – В чем отличие сочетания из п элементов по k от размещения из п элементов по k. Домашнее задание: прочитать п.33, выполнить № 769, № 771, № 783. З а д а ч а. В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить четырех мальчиков и трех девочек. Сколькими способами это можно сделать?
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 3; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.155.149 (0.009 с.) |

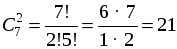 .
.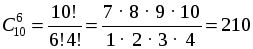 .
.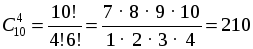
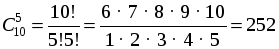
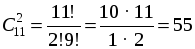 .
.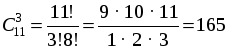 .
.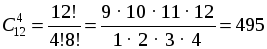 способов.
способов.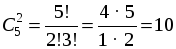 способов.
способов.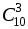 способов) и 2 журнала из 4 (
способов) и 2 журнала из 4 ( 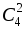 способов) – порядок выбора значения не имеет. Каждый выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу произведения равно:
способов) – порядок выбора значения не имеет. Каждый выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу произведения равно: