
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциялардың жұп немесе тақ екенін анықтаңдар.Содержание книги
Поиск на нашем сайте
Функциялардың жұп немесе тақ екенін анықтаңдар.
Мысалы: (үлгі) 1)
2)
3)
4)
5) 6) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1. 2. 3. 4. у 5. 6. 7. 8. 9. 10. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Таңба тұрақтылық аралығы
2.f 3. Мысалы:
1)
2) 1.y 2.y 3.y 4.y 5.y 6.y 7.y 8.y 9.y 10.y 1. y 2. y 3. y 4. y 5. y 6. y 7. y 8. y 9. y 10. y 1.y 2. y 3. y 4. y 5. y 6. y 7. y 8. y Функцияның ең кіші оң периоды.
Мысалы: 1) y=sin(
2) y=ctg(5x+195 5x= 3) y=cos(
4) 5) 6) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Мысалы: 1) y=2+ ( x = y=2+ 2) y= x + 3=
3) y=
y = y= 4)
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Қосынды және айырым түрінде берілген тригонометриялық функцияларды көбейтінді түрінде келтіру
Мысалы: 1) sin2 2) cos( 3) tg
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1. 2. 3. 4. 5. 1. 2. 3. 4. 5. 1. 2. 3. 4 . 5. Көбейтінді түрінде берілген тригонометриялық функцияларды қосынды немесе айрымы түріне келтіру. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Мысалы: 1) sin15 2) cos 3) sin52 4)
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15)
1)Функцияның анықталу облысы барлық нақты сандар жиыны 2) Мәндер жиыны 3) 4) Функция тақ, 5) 6)
Мысалы: 1. 1) Анықталу облысы 2)Мәндер облысы:
2. 1) Анықталу облысы 2) Мәндер облысы: 3. y = –2sinx( 1)анықталу облысы D(y) 2) мәндер облысы –1 2 5 3) функция периодты 4) F(-x)= –2sin( 4. y=2si 1)анықталу облысы D(y) 2)мәндер облысы 0 0 3)функция периодты 4)f(x)=2
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 50; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |


 Функция жұп
Функция жұп
 -функция жұп, себебі
-функция жұп, себебі  теңдігі орындалды.
теңдігі орындалды. - функция жұп, себебі
- функция жұп, себебі  -функция тақ, себебі
-функция тақ, себебі  теңдігі орындалды.
теңдігі орындалды. -функция тақ, себебі
-функция тақ, себебі  - функция жұп та, тақ та емес.
- функция жұп та, тақ та емес. - функция жұп та, тақ та емес.
- функция жұп та, тақ та емес.


 – функция жұп та, тақ та емес.
– функция жұп та, тақ та емес.






























 функциясының таңбасын интервалдар әдісімен таңбаны анықтау.
функциясының таңбасын интервалдар әдісімен таңбаны анықтау. 


 ;
; 

























 +3
+3









 функциясы үшін ең кіші оң период -2
функциясы үшін ең кіші оң период -2 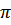
 функциясы үшін ең кіші оң период –
функциясы үшін ең кіші оң период – 



 y =sinx-тің ең кіші оң периоды 2π.
y =sinx-тің ең кіші оң периоды 2π. =2
=2  . Жауабы: ең кіші оң периоды 2
. Жауабы: ең кіші оң периоды 2 
 . Жауабы: ең кіші оң периоды
. Жауабы: ең кіші оң периоды 


 Ж: ең кіші оң периоды
Ж: ең кіші оң периоды 
 Ж: ең кіші оң периоды
Ж: ең кіші оң периоды 
 Ж: ең кіші оң периоды
Ж: ең кіші оң периоды 






























 функциясының кері функциясын анықта.
функциясының кері функциясын анықта. x-ті у арқылы өрнектейміз:
x-ті у арқылы өрнектейміз:
 :
:  у =
у = 
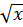 функциясына кері функция y =
функциясына кері функция y =  x-ті y арқылы өрнектейміз:
x-ті y арқылы өрнектейміз:
 функциясына кері функция y=
функциясына кері функция y= 

 =
=  –
– 
 –
–  функциясына кері функция y=
функциясына кері функция y= 

 –1
–1




























 -3
-3

 +
+ 

 = 2sin
= 2sin 
 –
–  =2cos
=2cos  cos(
cos( 
 =
=  =
= 
 ctg
ctg 

































































 Ж;
Ж; 

 30′
30′  -
- 














































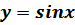 функциясы
функциясы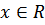
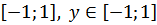
 функция периодты, ең кіші оң периоды
функция периодты, ең кіші оң периоды 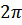

 функция бірсарынды өспелі
функция бірсарынды өспелі функция бірсарынды кемімелі
функция бірсарынды кемімелі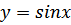 функция графигі синусоида деп аталады.
функция графигі синусоида деп аталады.


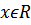

 .
.  , сонда
, сонда 

 .
.
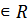

 (+3)
(+3) E(y)∊[1;5]
E(y)∊[1;5] ең кіші оң периодты 4
ең кіші оң периодты 4 


 2]
2] 2
2 




