
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторные величины. Понятие вектораСодержание книги
Поиск на нашем сайте
Векторы и действия над ними Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними. Некоторые физические величины (сила, скорость, ускорение) характеризуются не только числовым значением, но и направлением. Например, чтобы охарактеризовать движение тела в данный момент, недостаточно указать скорость движения, а нужно еще указать направление движения тела, т.е. направление скорости. Таким образом, скорость является векторной величиной. Другими примерами векторных величин могут служить сила притяжения, центробежное ускорение и т.п. Величины, при измерении которых необходимо учитывать их направление, называют векторными. Вектором называется направленный отрезок
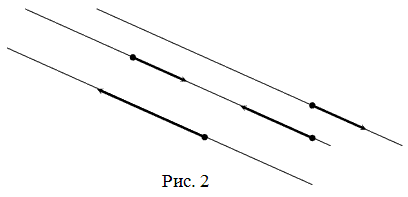
Вектор обозначается либо двумя большими буквами - своим началом и концом: Если начало и конец вектора совпадают, то такой вектор называется нулевым. Чаще всего нулевой вектор обозначается как Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2).
Два коллинеарных вектора Два коллинеарных вектора
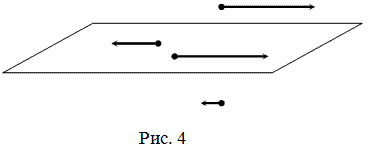
Векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости (рис. 4).
Два вектора всегда компланарны. Длиной (модулем) вектора Вектор, длина которого равна единице, называется единичным вектором или ортом. Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны. Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины:
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.235.177 (0.005 с.) |

 ; точка
; точка 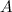 - начало, точка
- начало, точка 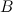 - конец вектора (рис. 1).
- конец вектора (рис. 1).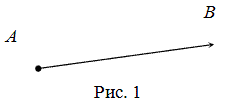
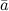 .
. .
.
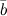 называются сонаправленными, если их направления совпадают:
называются сонаправленными, если их направления совпадают:  (рис.3а).
(рис.3а).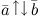 (рис. 3б).
(рис. 3б).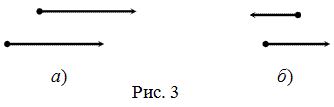
 . Длина нулевого вектора равна нулю.
. Длина нулевого вектора равна нулю.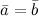 , если
, если 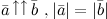 .
.


