
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні формули. Рівняння Шредінгера. Основні формули. Рентгенівське випромінюванняСодержание книги
Поиск на нашем сайте
Основні формули 1. Співвідношення невизначеностей Гейзенберга
де Dx, Dy, Dz – невизначеності координат x, y, z частинки; Dpx, Dpy, Dpz – невизначеності відповідних проекцій імпульсу частинки. 2. Співвідношення невизначеностей для енергії частинки
де DE – невизначеність енергії частинки; Dt, -час (тривалість) життя частинки у стані з даним значенням енергії.
28.1 Пучок електронів рухається вздовж осі 0X зі швидкістю v = 106 м/с, яка визначається з точністю до 0,01 % від її числового значення. Знайти невизначеність Dx координати електрона. (1,16×10-6 м) 28.2 Пилинка масою m = 10-12 кг має лінійні розміри порядку 10-6 м. Координату пилинки можна визначити з точністю до 0,01 її розмірів. Знайти невизначеність швидкості Dvx пилинки. (1,05×10-14 м/c) 28.3 Електронний пучок прискорюється в електронно-променевій трубці різницею потенціалів U = 500 В. Приймаючи, що невизначеність імпульса дорівнює 0,1 % від його числового значення, визначити невизначеність координати Dx електрона. (8,8 нм) 28.4 Електрон рухається в атомі водню по першій борівській орбіті зі швидкістю v = 2,18×106 м/с. Вважаючи, що невизначеність швидкості дорівнює 10% від її числового значення, знайти невизначеність Dx координати електрона. ( 5,31×10-10 м) 28.5 Електрон рухається в атомі водню по першій борівській орбіті. Нехай невизначеність координати електрона є порядку розмірів самого атома, тобто Dx = 10-10 м. Знайти невизначеність швидкості Dv руху електрона по орбіті. (1,16×106 м/с) 28.6 Кінетична енергія електрона в атомі водню Ек = 10 еВ. Використовуючи співвідношення невизначеностей, оцінити мінімальні лінійні розміри атома. ( 1,23×10-10 м) 28.7 Електрон знаходиться в нескінчено глибокій „потенціальній ямі” шириною ℓ = 100 пм. Використовуючи співвідношення невизначеностей, знайти мінімальну енергію Еmin електрона. (3,8 еВ) 28.8 У скільки разів довжина хвилі де Бройля l частинки менша невизначеності Dx її координати, яка відповідає відносній невизначеності імпульса в 1 %? (15,9) 28.9 Вважаючи, що невизначеність координати рухомої частинки Dx дорівнює довжині хвилі l де Бройля, визначити відносну неточність Dр/р імпульсу цієї частинки. (15,9 %) 28.10 Атом водню спочатку перебуває в основному стані, а потім переходить у збуджений стан, час життя в якому t = 10-8 с. Оцінити ширину DЕ енергетичного рівня атома в основному і збудженому станах. (0; 0,07 мкеВ)
28.11 Атом переходить із збудженого стану, в якому час життя t = 10-8 с, в основний стан, випромінюючи хвилю довжиною l = 0,6 мкм. Визначити природну ширину Dl спектральної лінії випромінювання атома. (0,02пм)
29. Рівняння Шредінгера Основні формули 1. Умова нормування хвильової функції y
де V – повний об’єм, в якому може перебувати частинка. 2. Ймовірність W знаходження частинки в заданому об’ємі V
де y - хвильова функція, яка описує стан частинки 3. Значення енергії частинки, En в одномірній прямокутній нескінченно глибокій потенціальній ямі
де m – маса частинки; ℓ - ширина потенціальної ями; n – квантове число. 4. Коефіцієнт прозорості D потенціального бар’єра прямокутної форми
де U – висота потенціального бар’єра; m – маса частинки; E – енергія частинки; ℓ- ширина бар’єра.
29.1 Хвильова функція, яка описує стан електрона в одномірній прямокутній нескінченно глибокій потенціальній ямі, має вигляд yn(x) = A sin kx + B cos kx. Ширина ями ℓ = 0,01 м. Визначити енергію електрона Е2 на другому енергетичному рівні. (1,4×10-14еВ) 29.2 Хвильова функція, що описує стан електрона в одномірній прямокутній нескінченно глибокій потенціальній ямі, має вигляд 29.3 Електрон знаходиться в одномірній прямокутній нескінченно глибокій потенціальній ямі. Знайти відношення різниці сусідніх енергетичних рівнів DЕn до енергії електрона Еn у таких випадках: 1) n = 1; 2) n = 10; 3) n = 100; 4) n = ¥. (3; 0,21; 0,0201; 0) 29.4 Електрон знаходиться в одномірній прямокутній нескінченно глибокій потенціальній ямі. Визначити різницю енергій двох сусідніх енергетичних рівнів DЕ2 при розмірах ями ℓ1 = 10-1 м і ℓ2 = 10-10 м. (18,6×10-17 еВ; 186,2 еВ) 29.5 Електрон знаходиться в одномірній прямокутній нескінченно глибокій потенціальній ямі. Обчислити імовірність W виявлення електрона в середній третині ями. (0,195) 29.6 Електрон в одномірній прямокутній нескінченно глибокій потенціальній ямі перебуває у збудженому стані (n = 4). Визначити імовірність W виявлення електрона в першій чверті ями. (0,250) 29.7 У додатному напрямку осі 0X рухаються електрон і протон з енергією Е = 4 еВ кожний і зустрічають на своєму шляху прямокутний потенціальний бар’єр висотою U = 9 еВ і шириною ℓ = 0,5 пм. Визначити відношення імовірностей We/Wp проходження електроном і протоном цього бар’єру. (1,62)
29.8 Електрон з енергією Е = 2 еВ рухається в додатному напрямку осі 0X і зустрічає на своєму шляху прямокутний потенціальний бар’єр висотою U = 12 еВ. Коефіцієнт прозорості бар’єра D = 0,02. Визначити ширину ℓ бар’єра. (0,12 нм) 29.9 Електрон з енергією Е рухається в додатному напрямку осі 0X і зустрічає на своєму шляху прямокутний потенціальний бар’єр висотою U і шириною ℓ = 0,5 нм. Коефіцієнт прозорості бар’єра D = 0,05. Визначити різницю енергій U - E. (0,34 еВ) 29.10 Нормована хвильова функція, що описує стан 1s-електрона в атомі водню має вигляд
|
||||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.92.5 (0.01 с.) |

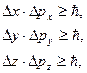
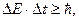
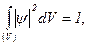
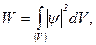
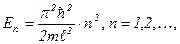
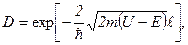
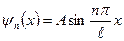 . Використовуючи умову нормування, визначити сталу А. (
. Використовуючи умову нормування, визначити сталу А. ( 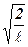 )
)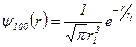 , де r – відстань електрона від ядра, r1 - радіус першої орбіти електрона. Визначити імовірність W виявлення електрона в атомі всередині сфери радіусом r = 0,021 r1. (1,03×10-5)
, де r – відстань електрона від ядра, r1 - радіус першої орбіти електрона. Визначити імовірність W виявлення електрона в атомі всередині сфери радіусом r = 0,021 r1. (1,03×10-5)


