Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет скорости и ускорения точки при координатном задании движении.Содержание книги
Поиск на нашем сайте
§4. Расчет скорости и ускорения точки при координатном задании движении.
Движение точки в декартовых осях координат задается функциями: x = x (t); y = y (t); z = z (t). Вектор скорости точки рассчитывается по формулам:
; ; ;
Вектор ускорения точки рассчитывается по формулам:
Для расчета траектории точки необходимо исключить время из уравнений движения точки.
§5. Расчет скорости и ускорения точки при естественном задании движения.
Оси (t, n, b) называются естественными осями траектории. Центр их всегда находится в точке, движение которой исследуется. Оси (t, n, b) друг относительно друга в пространстве расположены так же, как и оси (x, y, z) в правосторонней системе координат. Векторы
Соприкасающаяся плоскость строится по следующему правилу:
n рассматриваются два последовательных положения точки на траектории; n изображаются единичные векторы касательных осей n в исходной точке на векторах
Соприкасающаяся плоскость
пл. Q M2
M1
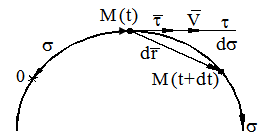
Нормальная плоскость строится перпендикулярно касательной оси. Спрямляющая плоскость строится перпендикулярно нормальной оси. При исследовании движения точки в естественных осях векторы скорости и ускорения точки раскладываются на составляющие вдоль этих осей. Разложение вектора скорости Из определения вектора скорости следует
Закон движения
Отсюда
Разложение вектора ускорения
Из определений вектора ускорения и соприкасающейся плоскости следует, что вектор ускорения лежит в соприкасающейся плоскости, т.е. Wbє0, следовательно
По определению
Можно показать, что выполняется
Величина r - называется радиусом кривизны траектории в данной точке. Это радиус окружности, которая строится так: на траектории выбираются три близкие точки М1, М2, М3 через которые проводится окружность
|
|||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 11; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.48.91 (0.01 с.) |

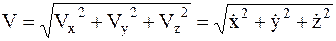 ;
;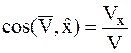 ;
; 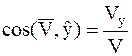 ;
; 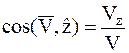 .
.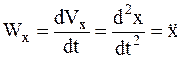 ;
; 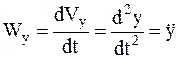 ;
; 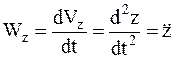 ;
;
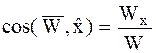 ;
; 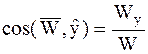 ;
; 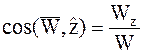 .
.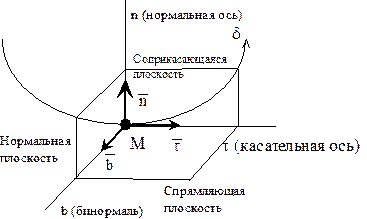
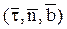 - единичные векторы или орты естественных осей. Очевидно, что
- единичные векторы или орты естественных осей. Очевидно, что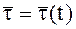 ;
; 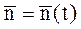 ;
; 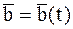 .
.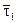 и
и 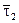 ;
;
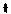 s в точке
s в точке 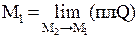
 t2
t2  t2
t2  t1
t1 
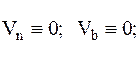
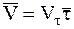
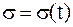
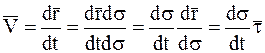

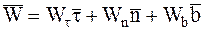

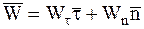
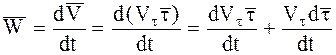
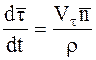 , тогда
, тогда 
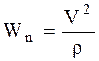 ;
;  ;
; 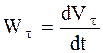 ;
; 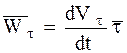 ;
; 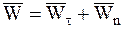
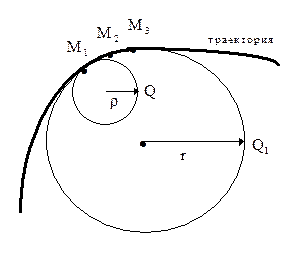
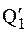 . Тогда окр.
. Тогда окр.