
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет ускорений точек тела при плоском движении методом полюса.Содержание книги
Поиск на нашем сайте
§14. Расчет ускорений точек тела при плоском движении методом полюса.
Рассматривается плоское движение тела. За полюс выбирается точка А. Предполагается, что движение ее известно, в частности, известно ускорение
WABВР WB WA
B
w A
Ранее, для скорости точки В была получена формула
Дифференцируя эту формулу по времени, найдем
Сопоставляя эту формулу с выводами, полученными при разложении плоского движения на составляющие, можно заключить следующее: Используя формулы вращательного движения, формулу для расчета ускорения точки В в развернутом виде можно записать так:
где Если движение полюса происходит по криволинейной траектории, то целесообразно разложить его ускорение на касательную и нормальную составляющие. Тогда для расчета ускорения точки В можно записать следующую формулу
§15. Сложное движение точки. Основные понятия и определения.
В ряде практических случаев движение точки по отношению к некоторой системе отсчета (условно неподвижной) может быть разложено на два «простых» составляющих движения. Как правило, эти движения известны. В связи с этим возникает задача: рассчитать кинематику основного - сложного движения точки, зная кинематику «простых» составляющих движений.
_
В общем виде эта задача формулируется так. Движение точки М рассматривается в двух системах отсчета: условно неподвижной системе (x, y, z) и движущейся относительно нее произвольным образом системе (x', y', z'). Условно неподвижная система отсчета (x, y, z) называется абсолютной. Движение точки в ней так же называется абсолютным и физические характеристики этого движения снабжаются индексом «a» (Va, Wa и т.д.). Система отсчета (x', y', z') называется переносной (она как бы переносит в своем движении рассматриваемую точку). Движение точки пространства переносной системы, через которую в данный момент времени проходит исследуемый объект (точка М) называется переносным движением точки М и физические характеристики этого движения снабжаются индексом «e» (Ve, We и т.д.). Движение точки М по отношению к системе отсчета (x', y', z') называется относительным движением точки М. Физические характеристики этого движения снабжаются индексом «r» (Vr, Wr и т.д.). Считается, что относительное и переносное движения точки заданы. Необходимо получить математические формулы для расчета результирующего - сложного движения точки.
В основе расчета кинематики сложного движения точки лежат две теоремы: теорема сложения скоростей и теорема сложения ускорений. Строгое математическое доказательство этих теорем достаточно сложно и громоздко, поэтому для краткости дадим лишь исходную постановку и конечный результат этих вопросов.
|
||||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 9; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.162.155 (0.009 с.) |

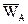 . Необходимо вывести формулу для расчета ускорения произвольной точки В тела.
. Необходимо вывести формулу для расчета ускорения произвольной точки В тела. __ __ __
__ __ __
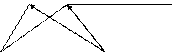



 y WAB B
y WAB B A __ __
A __ __ WA WABОС
WA WABОС
 __
__
 x WA
x WA
 e
e 
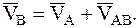

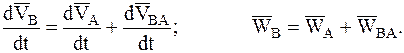
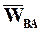 - ускорение точки В в относительном вращательном движении тела вокруг полюса.
- ускорение точки В в относительном вращательном движении тела вокруг полюса.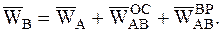
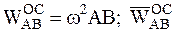 - направлен вдоль АВ к полюсу,
- направлен вдоль АВ к полюсу, 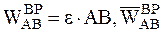 перпендикулярен АВ и направлен в сторону вращения, если оно ускоренное и в обратную сторону, если - замедленное .
перпендикулярен АВ и направлен в сторону вращения, если оно ускоренное и в обратную сторону, если - замедленное .

 M
M
 _
_ r
r

 z _ y'
z _ y'

 rA z' O1
rA z' O1


 rO x'
rO x' y
y x
x


