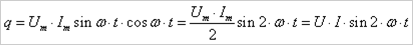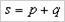Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия возникновения и особенности резонансов напряжения и токов.Содержание книги
Поиск на нашем сайте
Резонанс напряжений Если последовательно с генератором соединить конденсатор и катушку индуктивности, то, при условии равенства их реактивных сопротивлений, возникнет резонанс напряжений. При этом активная часть Z должно быть как можно меньшей.
Стоит отметить, что индуктивность и емкость обладает только реактивными качествами лишь в идеализированных примерах. В реальных же цепях и элементах всегда присутствует активное сопротивление проводников, хоть оно и крайне мало. При резонансе происходит обмен энергией между дросселем и конденсатором. В идеальных примерах при первоначальном подключении источника энергии (генератора) энергия накапливается в конденсаторе (или дросселе) и после его отключения происходят незатухающие колебания за счет этого обмена. Напряжения на индуктивности и емкости примерно одинаковы, согласно закону Ома: U=I/X. Где X — это Xc емкостное или XL индуктивное сопротивление соответственно. Цепь, состоящую из индуктивности и емкости, называют колебательным контуром. Его частота вычисляется по формуле: Так как реактивное сопротивление зависит от частоты, то сопротивление индуктивности с ростом частоты увеличивается, а у ёмкости падает. Когда сопротивления равны, то общее сопротивление сильно снижается, что отражено на графике:
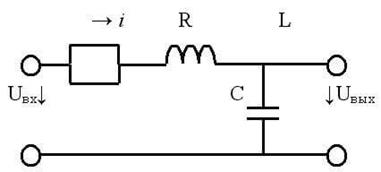
Основными характеристиками контура являются добротность (Q) и частота. Если рассмотреть контур в качестве четырехполюсника, то его коэффициент передачи после несложных вычислений сводится к добротности: K=Q
А напряжение на выводах цепи увеличивается пропорционально коэффициенту передачи (добротности) контура. Uк=Uвх*Q При резонансе напряжений, чем выше добротность, тем больше напряжение на элементах контура будет превышать напряжение подключенного генератора. Напряжение может повышаться в десятки и сотни раз. Это отображено на графике:
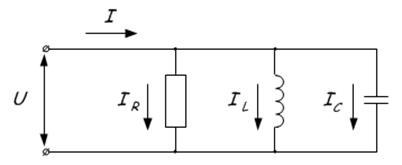
Потери мощности в контуре обусловлены только наличием активного сопротивления. Энергия из источника питания берется только для поддержания колебаний. Коэффициент мощности будет равен: cosФ=1. Эта формула показывает, что потери происходят за счет активной мощности: S=P/Cosф Резонанс токов Резонанс токов наблюдается в цепях, где индуктивность и емкость соединены параллельно.
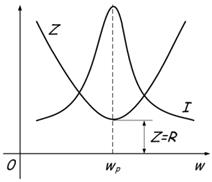
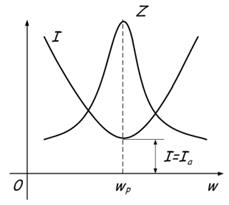
Явление заключается в протекании токов большой величины между конденсатором и катушкой, при нулевом токе в неразветвленной части цепи. Это объясняется тем, что при достижении резонансной частоты общее сопротивление Z возрастает. Или простым языком звучит так – в точке резонанса достигается максимальное общее значение сопротивления Z, после чего одно из сопротивлений увеличивается, а другое снижается в зависимости от того растет или снижается частота. Это наглядно отображено на графике:
В общем, всё аналогично предыдущему явлению, условия возникновения резонанса токов следующие: 1.Частота питания аналогична резонансной у контура. 2.Проводимости у индуктивности и ёмкости по переменному току равны BL=Bc, B=1/X.
Активная, реактивная и полная мощность в цепи переменного тока. Активная мощность В цепи с чисто активным сопротивлением она равна:
Где
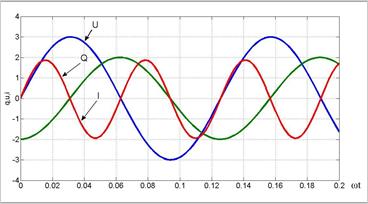
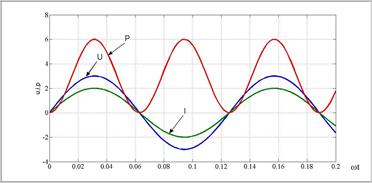
Отличие реактивной мощности от активной В цепи, где есть реактивное сопротивление (возьмем для примера индуктивное) значение мгновенной мощности равно: Соответственно Данное выражение показывает, что реактивная энергия содержит только переменную часть, которая изменяется с двойной частотой, а ее среднее значение равно нулю
Если ток и напряжение имеют синусоидальную форму и сеть содержит элементы типа R-L или R-C, то в таких сетях кроме преобразования энергии в активном элементе R вдобавок еще и изменяется энергия электрического и магнитного полей в реактивных элементах L и C. В таком случае полная мощность сети будет равна сумме:
|
||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

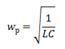 Период колебаний определяется по формуле Томпсона:
Период колебаний определяется по формуле Томпсона: 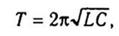
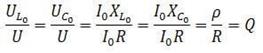

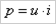 Если принять
Если принять  и
и  тогда выйдет:
тогда выйдет:
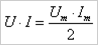 . Исходя из выражений выше — активная энергия состоит из двух частей — постоянной
. Исходя из выражений выше — активная энергия состоит из двух частей — постоянной  и переменной
и переменной  , которая меняется с двойной частотой. Среднее ее значение
, которая меняется с двойной частотой. Среднее ее значение 
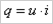
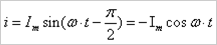 в итоге получим:
в итоге получим: