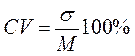Математико-статистический анализ

Анализ первичных статистик.

Для определения способов математико-статистической обработки, прежде всего, необходимо оценить характер распределения по всем используемым параметрам. Для параметров, имеющих нормальное распределение или близкое к нормальному, можно использовать методы параметрической статистики, которые во многих случаях являются более мощными, чем методы непараметрической статистики. Достоинством последних является то, что они позволяют проверить статистические гипотезы независимо от формы распределения.

Одним из важнейших в математической статистике является понятие нормального распределения. Нормальное распределение – модель варьирования некоторой случайной величины, значения которой определяются множеством одновременно действующих независимых факторов. Число таких факторов велико, а эффект каждого из них в отдельности очень мал. Такой характер взаимовлияний весьма характерен для психических явлений, поэтому исследователь в области психологии чаще всего выявляет нормальное распределение. Однако, так бывает не всегда, поэтому в каждом случае форма распределения должна быть проверена.

Важнейшими первичными статистиками являются:

а) средняя арифметическая – величина, сумма отрицательных и положительных отклонений от которой равна нулю. В статистике ее обозначают буквой М или .

б) среднее квадратичное отклонение (обозначаемое греческой буквой σ (сигма) и называемое также основным, или стандартным отклонением) – мера разнообразия входящих в группу объектов; она показывает, на сколько в среднем отклоняется каждая варианта (конкретное значение оцениваемого параметра) от средней арифметической. Чем сильнее разбросаны варианты относительно средней, тем большим оказывается и квадратичное отклонение.

в) коэффициент вариации – частное от деления сигмы на среднюю, умноженное на 100%. Обозначается CV.

Сигма – величина именованная и зависит не только от степени варьирования, но и от единиц измерения. Поэтому по сигме можно сравнивать изменчивость лишь одних и тех же показателей, а сопоставлять сигмы разных признаков по абсолютной величине нельзя. Для того, чтобы сравнить по уровню изменчивости признаки любой размерности (выраженные в различных единицах измерения) и избежать влияния масштаба измерения средней арифметической на величину сигмы применяют коэффициент вариации, который представляет собой по существу приведение к одинаковому масштабу величины σ.

Для нормального распределения известны точные количественные зависимости частот и значений позволяющие прогнозировать появление новых вариант:

1) Слева и справа от средней арифметической лежит 50 % вариант.

2) В интервале от M – σ до M + σ лежат 68.7 % всех вариант.

3) В интервале от M – 1.96σ до M + 1. 96σ лежат 95 % вариант.

Таким образом, ориентируясь на эти характеристики нормального распределения, можно оценить степень близости к нему рассматриваемого распределения.

Следующими по важности являются такие первичные статистики как коэффициент асимметрии и эксцесс. Коэффициент асимметрии – показатель скошенности распределения в левую и правую сторону по оси абсцисс. Если правая ветвь кривой длиннее левой – говорят о положительной асимметрии, в противоположном случае – об отрицательной. Эксцесс – показатель островершинности. Кривые более высокие в средней части, островершинные, называются эксцессивными, у них большая величина эксцесса. При уменьшении величины эксцесса, кривая становиться всё более плоской, приобретая вид плато, а затем и седловины – с прогибом в средней части.

Эти параметры позволяют составить первое приближенное представление о характере распределения:

1) у нормального распределения редко можно обнаружить коэффициент асимметрии близкий к единице и более единицы (и -1, и +1);

2) эксцесс у признаков с нормальным распределением обычно имеет величину в диапазоне 2 – 4.

Подчеркнем, что это только приблизительная оценка. Точную и строгую оценку нормальности распределения можно получить, используя один из существующих методов проверки. (См., например, книгу Г.В. Суходольского “Основы математической статистики для психологов”, Л., 1972. Главы 2 и 5.)

Начать с анализа первичных статистик надо ещё и по той причине, что они весьма чувствительны к наличию выпадающих вариант. На практике же, очень большие эксцесс и асимметрия являются индикатором ошибок при подсчётах вручную или ошибок при введении данных через клавиатуру при компьютерной обработке. Существует правило, согласно которому все расчёты вручную должны выполняться дважды (особенно ответственные – трижды), причём желательно разными способами, с вариацией последовательности обращения к числовому массиву.

По части никогда не удаётся полностью охарактеризовать целое, всегда остаётся вероятность того, что оценка генеральной совокупности на основе выборочных данных недостаточно точна, имеет некоторую большую или меньшую ошибку. Такие ошибки, представляющие собой ошибки обобщения, экстраполяции, связанные с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность, называются ошибками репрезентативность. Репрезентативность – степень соответствия выборочных показателей генеральными параметрам.

Статические ошибки репрезентативности показывают в каких пределах могут отклоняться от параметров генеральной совокупности (от математического ожидания или истинных значений) наши честные определения, полученные на основании конкретных выборок. Очевидно, что величина ошибки тем больше, чем больше варьирование признака и чем меньше выборка. Это и отражено в формулах для вычисления статических ошибок, характеризующих варьирование выборочных показателей вокруг их генеральных параметров.

В число первичных статистик входит статистическая ошибка средней арифметической. Формула для её вычисления такова:

где: m_M – ошибка средней, σ – сигма, n – число значений признака.