
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 13. Пересечение плоскости с гранным геометрическим телом и с цилиндром. Построение проекций и натуральной величины наклонного сечения проецирующей плоскостью.Содержание книги
Поиск на нашем сайте Сечение гранного тела.
Если секущая плоскость будет проходить через образующие, то в сечении получим параллельные прямые, если через направляющие, то - окружность. Все остальные сечения цилиндра будут эллипсами. Построение сечения цилиндра фронтально проецирующей плоскостью рассмотрено на рис. 8.2. Натуральную величину сечения построим по точкам. Отметим на чертеже точки, соответствующие большой АВ и малой CD осям эллипса
Вопрос 14. Наклонные сечения конуса и шара. Построение проекций и натуральной величины наклонного сечения проецирующей плоскостью.
Если секущая плоскость будет проходить через образующую (прямую), то в сечении получим треугольник, если через направляющую (окружность) - окружность.
Натуральную величину сечения можно построить по законам построения эллипса. Для этого на оси х откладываем большую ось эллипса АВ и малую CD. Причем, малая ось эллипса определяется как хорда (CD) параллели, делящей пополам фронтальную проекцию сечения.
Сечение шара. Как известно, любое сечение шара плоскостью является кругом. В зависимости от положения секущей плоскости, окружность, ограничивающая фигуру сечения, может спроецироваться в:
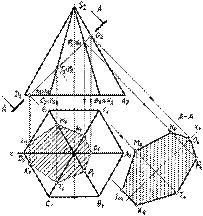
Билет 15. Построение проекций и натуральной величины наклонного сечения плоскостью общего положения на примере многогранника и конуса. См. билет 13 и 14. Билет 16. Построение точки пересечения прямой с поверхностью вращения. Пересечение многогранника с поверхностью вращения на примере соосных конуса и шестигранной призмы.(зад.56,59)
Искомые точки А (А 1, А 2), B (В 1, В 2), C (С 1, С 2), D (D 1, D 1) найдены при помощи вспомогательной горизонтальной плоскости W (W 2), которая рассекает поверхность тора по параллелям радиусов О 1 и О 2. Количество точек пересечения прямой с поверхностью в общем случае определяет порядок поверхности. Действительно, тор - поверхность четвертого порядка, и прямая пересекает его поверхность в четырех точках A, B, C, D. В приведенных примерах в качестве вспомогательных плоскостей использовались проецирующие плоскости. Рассмотрим ряд случаев, в которых более целесообразно в качестве вспомогательных плоскостей использовать плоскости общего положения.
|
||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 Сечение цилиндра.
Сечение цилиндра.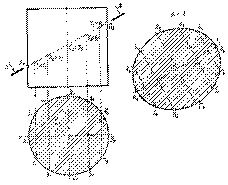
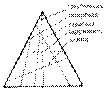 Сечение конуса.
Сечение конуса.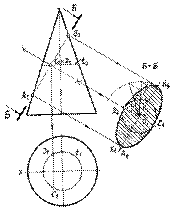 На рис. 8.4 выполнен чертеж конуса, и показана секущая плоскость Б - Б, которая пересекает все образующие данного конуса. Следовательно, фигура сечения будет ограничена эллипсом, а отрезок А 2 B 2 является его фронтальной проекцией
На рис. 8.4 выполнен чертеж конуса, и показана секущая плоскость Б - Б, которая пересекает все образующие данного конуса. Следовательно, фигура сечения будет ограничена эллипсом, а отрезок А 2 B 2 является его фронтальной проекцией Так как сечение шара - круг (рис. 8.7), то построение его натуральной величины сводится к определению радиуса окружности. Участок линии сечения А 3 В 3 является диаметром этой окружности. Поэтому для построений на новую ось х 1 линиями связи переносятся точки О и В, после чего радиусом, равным расстоянию между ними, проводится окружность - граница фигуры сечения А - А.
Так как сечение шара - круг (рис. 8.7), то построение его натуральной величины сводится к определению радиуса окружности. Участок линии сечения А 3 В 3 является диаметром этой окружности. Поэтому для построений на новую ось х 1 линиями связи переносятся точки О и В, после чего радиусом, равным расстоянию между ними, проводится окружность - граница фигуры сечения А - А.
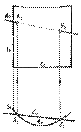 Построение точки встречи прямой общего положения с проецирующей поверхностью
Построение точки встречи прямой общего положения с проецирующей поверхностью 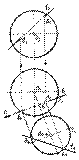 Построим точки встречи прямой 1 с поверхностью сферы. Заключим прямую 1 в горизонтально проецирующую плоскость Г (Г 1 º 1 1). Эта плоскость пересечет сферу по окружности, которая на плоскость П 2 спроецируется в эллипс с большой С 2 D 2 и малой Е 2 F 2 осями. В пересечении фронтальной проекции 1 2 прямой 1 с эллипсом получим А 2 и В 2 -фронтальные проекции искомых точек.
Построим точки встречи прямой 1 с поверхностью сферы. Заключим прямую 1 в горизонтально проецирующую плоскость Г (Г 1 º 1 1). Эта плоскость пересечет сферу по окружности, которая на плоскость П 2 спроецируется в эллипс с большой С 2 D 2 и малой Е 2 F 2 осями. В пересечении фронтальной проекции 1 2 прямой 1 с эллипсом получим А 2 и В 2 -фронтальные проекции искомых точек. 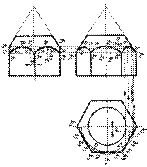

 Пример построения точек встречи горизонтальной прямой 1 с поверхностью тора.
Пример построения точек встречи горизонтальной прямой 1 с поверхностью тора.


