
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 8. Поверхности вращения. Особые линии поверхностей вращения. Поверхности вращения 2-го и 4-го порядка. Принадлежность точки поверхности вращения.Содержание книги
Поиск на нашем сайте
Определитель: Ф (l, i)[ l Æi ]. На чертеже поверхность вращения задается своим очерком. Очерком поверхности называются линии, которые ограничивают области ее проекций. При вращении каждая точка образующей описывает окружность, плоскость которой перпендикулярна оси. Соответственно, линия пересечения поверхности вращения плоскостью, перпендикулярной оси, является окружностью. Такие окружности называют параллелями (рис. 3.15). Параллель наибольшего радиуса называют экватором, наименьшего - горлом. Плоскость, проходящую через ось поверхности вращения, называют меридиональной, линию ее пересечения с поверхностью враще- ния - меридианом. Меридиан, лежащий в плоскости, параллельной плоскости проекций, называют главным меридианом. наиболее часто встречаются следующие поверхности вращения: цилиндрическая, коническая, сферическая, торовая.
Определитель: Ф (l ½½ i)[ l Æi ].
Определитель: Ф (l Ç i)[ l Æi ].
Принадлежность точки поверхности. Точка принадлежит поверхности, если она расположена на линии, принадлежащей поверхности. На поверхностях вращения в качестве линий удобно использовать окружности (параллели).
Вопрос 9. Поверхности с двумя направляющими и плоскостью параллелизма. Винтовые линии и поверхности. Эти поверхности образуются движением прямолинейной образующей по двум направляющим. Образующая во время своего движения все время остается параллельной некоторой плоскости, называемой плоскостью параллелизма. Определитель: Ф (l, a, b) [ l ½½ Г ].
На рис.3.20-б показана косая плоскость, для которой направляющими служат две скрещивающиеся прямые а и b, а в качестве плоскости параллелизма принята горизонтальная плоскость проекций П 1. Определитель: Ф (l, a Æ b)[ l ½½ П 1].
Определитель: Ф (l, k, t) [ l ½½ П 2].
Определитель: Ф (l, a, k) [ l ½½ Г ]. Винтовая линия. Если точка будет равномерно перемещаться по прямой, а прямая равномерно перемещаться по оси, то точка при этом опишет пространственную прямую, которая называется цилиндрической винтовой линией. Винтовая линия бывает правого и левого хода.
Если точка, вращаясь по часовой стрелке, удаляется от наблюдателя, то винт. линия правого хода. Если точка, вращаясь по часовой стрелке, приближается к наблюдателю, то винт. Линия левого хода. Расстояние между 2мя соседними точками винтовой линии расположенными на одной прямой паралл оси наз. шагом винтовой линии. Винтовые пов-ти.
|
||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 62; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.64.51 (0.009 с.) |

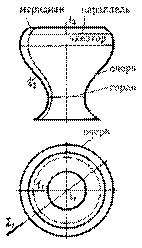 Поверхностью вращения называют поверхность, получающуюся от вращения некоторой образующей линии 1 вокруг неподвижной прямой i - оси вращения поверхности.
Поверхностью вращения называют поверхность, получающуюся от вращения некоторой образующей линии 1 вокруг неподвижной прямой i - оси вращения поверхности.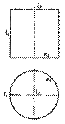 Цилиндрическую поверхность вращения можно рассматривать, как частный случай поверхности, изображенной на рис.3.1. В качестве направляющей а следует взять окружность, а в качестве прямой b - ось i (рис.3.16). Тогда получим, что образующая l, параллельная оси i, вращается вокруг последней.
Цилиндрическую поверхность вращения можно рассматривать, как частный случай поверхности, изображенной на рис.3.1. В качестве направляющей а следует взять окружность, а в качестве прямой b - ось i (рис.3.16). Тогда получим, что образующая l, параллельная оси i, вращается вокруг последней.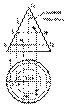 Коническую поверхность вращения получим, вращая прямолинейную образующую l вокруг оси i. При этом образующая l пересекает ось i в точке S, называемой вершиной конуса (рис.3.17).
Коническую поверхность вращения получим, вращая прямолинейную образующую l вокруг оси i. При этом образующая l пересекает ось i в точке S, называемой вершиной конуса (рис.3.17). Сферическая поверхность образуется за счет вращения окружности вокруг оси, проходящей через центр окружности и лежащей в ее плоскости (рис.3.18). Экватор и меридианы сферической поверхности являются равными между собой окружностями. Поэтому при ортогональном проецировании на любую плоскость сферическая поверхность проецируется в круги.
Сферическая поверхность образуется за счет вращения окружности вокруг оси, проходящей через центр окружности и лежащей в ее плоскости (рис.3.18). Экватор и меридианы сферической поверхности являются равными между собой окружностями. Поэтому при ортогональном проецировании на любую плоскость сферическая поверхность проецируется в круги.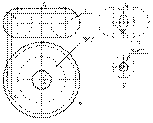 Торовая поверхность. При вращении окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, образуется поверхность, называемая торовой (рис.3.19).
Торовая поверхность. При вращении окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, образуется поверхность, называемая торовой (рис.3.19). Косая плоскость.
Косая плоскость. 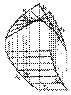 Цилиндроид
Цилиндроид 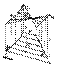 Коноид
Коноид 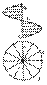 Винтовую поверхность можно рассматривать как частный случай коноида. Прямолинейная образующая перемещается по двум направляющим, одна из которых кривая (винтовая линия или гелиса), вторая - прямая (ось винтовой линии). Такую поверхность называют геликоидом.
Винтовую поверхность можно рассматривать как частный случай коноида. Прямолинейная образующая перемещается по двум направляющим, одна из которых кривая (винтовая линия или гелиса), вторая - прямая (ось винтовой линии). Такую поверхность называют геликоидом. 


