
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 4. Пересечение прямой и плоскости (3 случая). (зад.30,32)Содержание книги
Поиск на нашем сайте
Вопрос 2. Линии. Классификация линий. Прямая линия. Классификация прямых по расположению относительно друг друга и по расположению относительно плоскостей проекций. Принадлежность точки прямой. (зад.14,13) Любую линию можно рассматривать как результат перемещения некоторой точки в пространстве. При этом все множество линий можно разделить на прямые, кривые и пространственные. Прямую можно задать на чертеже в виде отрезка. Между длинами отрезка АВ и А1В1 имеется зависимость А1В1=АВcosфи, где Фи - угол между отрезком и плоскостью проекций. При фи = 0о отрезок проецируется в натуральную величину, при фи=90о – в точку. Кривые: циркульные и лекальные. Циркульные: эллипс, парабола, гипербола, окружность. Пространственные: винтовая линия. Взаимное расположение прямых.
Если прямые параллельны, то их одноименные проекции также параллельны. Если прямые скрещиваются, то их одноименные проекции могут пересекаться или на одной проекции пересекаться, а на второй - быть параллельными. Расположение прямых относ. Плоск.пр-ии. Прямые: общего и частного положения. Прямой общего положения называют прямую, не параллельную ни одной из данных плоскостей проекций. Любой отрезок такой прямой проецируется в данной системе плоскостей проекций искаженно. Искаженно проецируются и углы наклона этой прямой к плоскостям проекций. К прямым частного положения относятся прямые, параллельные одной или двум плоскостям проекций. Различают три основные линии уровня: горизонталь, фронталь и профильную линии. Горизонталью называют любую линию, параллельную горизонтальной плоскости проекций. Любой отрезок горизонтали проецируется на П1 без искажения. В ист.величину проецируется и угол наклона горизонтали к П2. Фронталью называют линию, параллельную фронтальной плоскости проекций. Любой отр.фронтали проецируется без искажения на П2. Угол наклона фронтали к П1 проецируется на П2 без искажения.
Профильной линией называют линию, параллельную профильной плоскости проекций. Любой отрезок профильной линии (прямой) проецируется на профильную плоскость в истинную величину. На эту же плоскость проецируются в истинную величину и углы наклона профильной прямой к плоскостям проекций П 1 и П 2 Прямая паралл. 2м пл-тям проекции будет перп. 3ей и наз. проецирующей прямой. Прямая перп. П1 – гориз.проец., П2-фронт.проец., П3-проф.проец. Принадлежность прямой точке. Точка принадлежит прямой, если соответствующие проекции точки расположены на соответствующих проекциях прямых.
Вопрос 3. Плоскость, задание на чертеже. Классификация плоскостей по расположению относительно плоскостей проекций. Принадлежность точки и прямой плоскости. Главные линии плоскости. Плоскость можно рассматривать как результат перемещения прямолинейной образующей l, все время оставаясь параллельной прямой b, вдоль направляющей а. При этом а является также прямой (рис.3.5). Определитель плоскости записывается следующим образом: F (l, а)[ l ½½ b ].
Всякий дополнительный элемент (точка, прямая), взятый произвольно, как правило, не будет принадлежать этой плоскости. Определитель: S (A, b)[ A Ëb ].
Класс. пл-тей относ. пл-тей проекции. Пл-ти: общего и частного положения Пл-ть перп. Одной пл-ти проекции наз проецирующей. Пл-ть перп. П1 – гориз проец, П2-фронт проец,П3 – проф проец. Пл-ть перп. 2м плоскостям проекции будет паралл 3ей и наз. плоскостью уровня. Пл-ть паралл. П1-гориз. Пл-ть уровня, П2- фронт.п.ур., П3 – проф.пл.ур. Принадлежность точки, прямой плоскости. Прямая принадлежит пл-ти, если она проходит через 2 точки, принадл. пл-ти. Точка принадлежит пл-ти, если она расположена на прямой, принадл. пл-ти. Главные линии плоскости. ..наз. прямые уровня принадл. пл-ти, а также линии наибольшего наклона к плоскости проекции. (задача 20) Линии наиб.наклона к пл-тям проекции – прямые принадл.пл-ти и перп линиям уровня пл-ти. Линией ската или л.наиб накл к П1 наз прямую принадл пл-ти и перп горизонтали пл-ти. Линией наиб.наклона к П2 наз. прямую принадл пл-ти и перпфронтали пл-ти. Пространственные кривые. Цилиндрическая винтовая линия
Для построения конической винтовой линии (рис.2.14) изобразим некоторое число положений прямой, равномерно отстоящих друг от друга (в данном случае 12). Положение точки, движущейся вдоль прямой, будем фиксировать так, чтобы движение вдоль прямой было пропорционально угловому перемещению вокруг оси. Горизонтальной проекцией конической винтовой линии будет спираль Архимеда. Фронтальной проекцией - синусоида с затухающей амплитудой. Получили левую винтовую линию.
Сечение гранного тела.
Если секущая плоскость будет проходить через образующие, то в сечении получим параллельные прямые, если через направляющие, то - окружность. Все остальные сечения цилиндра будут эллипсами. Построение сечения цилиндра фронтально проецирующей плоскостью рассмотрено на рис. 8.2. Натуральную величину сечения построим по точкам. Отметим на чертеже точки, соответствующие большой АВ и малой CD осям эллипса
Сечение шара. Как известно, любое сечение шара плоскостью является кругом. В зависимости от положения секущей плоскости, окружность, ограничивающая фигуру сечения, может спроецироваться в:
Билет 15. Построение проекций и натуральной величины наклонного сечения плоскостью общего положения на примере многогранника и конуса. См. билет 13 и 14. Билет 16. Построение точки пересечения прямой с поверхностью вращения. Пересечение многогранника с поверхностью вращения на примере соосных конуса и шестигранной призмы.(зад.56,59)
Искомые точки А (А 1, А 2), B (В 1, В 2), C (С 1, С 2), D (D 1, D 1) найдены при помощи вспомогательной горизонтальной плоскости W (W 2), которая рассекает поверхность тора по параллелям радиусов О 1 и О 2. Количество точек пересечения прямой с поверхностью в общем случае определяет порядок поверхности. Действительно, тор - поверхность четвертого порядка, и прямая пересекает его поверхность в четырех точках A, B, C, D. В приведенных примерах в качестве вспомогательных плоскостей использовались проецирующие плоскости. Рассмотрим ряд случаев, в которых более целесообразно в качестве вспомогательных плоскостей использовать плоскости общего положения.
Вопрос 2. Линии. Классификация линий. Прямая линия. Классификация прямых по расположению относительно друг друга и по расположению относительно плоскостей проекций. Принадлежность точки прямой. (зад.14,13) Любую линию можно рассматривать как результат перемещения некоторой точки в пространстве. При этом все множество линий можно разделить на прямые, кривые и пространственные. Прямую можно задать на чертеже в виде отрезка. Между длинами отрезка АВ и А1В1 имеется зависимость А1В1=АВcosфи, где Фи - угол между отрезком и плоскостью проекций. При фи = 0о отрезок проецируется в натуральную величину, при фи=90о – в точку.
Кривые: циркульные и лекальные. Циркульные: эллипс, парабола, гипербола, окружность. Пространственные: винтовая линия. Взаимное расположение прямых.
Если прямые параллельны, то их одноименные проекции также параллельны. Если прямые скрещиваются, то их одноименные проекции могут пересекаться или на одной проекции пересекаться, а на второй - быть параллельными. Расположение прямых относ. Плоск.пр-ии. Прямые: общего и частного положения. Прямой общего положения называют прямую, не параллельную ни одной из данных плоскостей проекций. Любой отрезок такой прямой проецируется в данной системе плоскостей проекций искаженно. Искаженно проецируются и углы наклона этой прямой к плоскостям проекций. К прямым частного положения относятся прямые, параллельные одной или двум плоскостям проекций. Различают три основные линии уровня: горизонталь, фронталь и профильную линии. Горизонталью называют любую линию, параллельную горизонтальной плоскости проекций. Любой отрезок горизонтали проецируется на П1 без искажения. В ист.величину проецируется и угол наклона горизонтали к П2. Фронталью называют линию, параллельную фронтальной плоскости проекций. Любой отр.фронтали проецируется без искажения на П2. Угол наклона фронтали к П1 проецируется на П2 без искажения. Профильной линией называют линию, параллельную профильной плоскости проекций. Любой отрезок профильной линии (прямой) проецируется на профильную плоскость в истинную величину. На эту же плоскость проецируются в истинную величину и углы наклона профильной прямой к плоскостям проекций П 1 и П 2 Прямая паралл. 2м пл-тям проекции будет перп. 3ей и наз. проецирующей прямой. Прямая перп. П1 – гориз.проец., П2-фронт.проец., П3-проф.проец. Принадлежность прямой точке. Точка принадлежит прямой, если соответствующие проекции точки расположены на соответствующих проекциях прямых.
Вопрос 3. Плоскость, задание на чертеже. Классификация плоскостей по расположению относительно плоскостей проекций. Принадлежность точки и прямой плоскости. Главные линии плоскости. Плоскость можно рассматривать как результат перемещения прямолинейной образующей l, все время оставаясь параллельной прямой b, вдоль направляющей а. При этом а является также прямой (рис.3.5). Определитель плоскости записывается следующим образом: F (l, а)[ l ½½ b ].
Всякий дополнительный элемент (точка, прямая), взятый произвольно, как правило, не будет принадлежать этой плоскости. Определитель: S (A, b)[ A Ëb ].
Класс. пл-тей относ. пл-тей проекции. Пл-ти: общего и частного положения Пл-ть перп. Одной пл-ти проекции наз проецирующей. Пл-ть перп. П1 – гориз проец, П2-фронт проец,П3 – проф проец. Пл-ть перп. 2м плоскостям проекции будет паралл 3ей и наз. плоскостью уровня. Пл-ть паралл. П1-гориз. Пл-ть уровня, П2- фронт.п.ур., П3 – проф.пл.ур. Принадлежность точки, прямой плоскости. Прямая принадлежит пл-ти, если она проходит через 2 точки, принадл. пл-ти. Точка принадлежит пл-ти, если она расположена на прямой, принадл. пл-ти. Главные линии плоскости. ..наз. прямые уровня принадл. пл-ти, а также линии наибольшего наклона к плоскости проекции. (задача 20) Линии наиб.наклона к пл-тям проекции – прямые принадл.пл-ти и перп линиям уровня пл-ти. Линией ската или л.наиб накл к П1 наз прямую принадл пл-ти и перп горизонтали пл-ти. Линией наиб.наклона к П2 наз. прямую принадл пл-ти и перпфронтали пл-ти. Вопрос 4. Пересечение прямой и плоскости (3 случая). (зад.30,32) 1). Пересечение проецирующей пр-ой с пл-тью общего положения.
2). Пересечение проецирующей пл-ти с прямой общ.положения. построим точку встречи фронтально проецирующей плоскости Q с прямой общего положения n (рис.7.4). Пусть n Ç Q = = М. М 2 - фронтальная проекция искомой точки М должна лежать на фронтальной проекции П 2 зад. 30
1) через прямую проводят вспомогательную плоскость F; Зад.32.
|
|||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.22 (0.012 с.) |

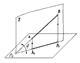
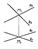 Прямые в пространстве могут пересекаться, быть взаимно параллельными (пересекаться в бесконечно удаленной точке) и скрещиваться.
Прямые в пространстве могут пересекаться, быть взаимно параллельными (пересекаться в бесконечно удаленной точке) и скрещиваться.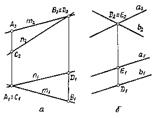
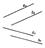 Если прямые пересекаются, то их одноименные проекции также пересекаются, причем точки пересечения одноименных проекций таких прямых лежат на одной линии связи
Если прямые пересекаются, то их одноименные проекции также пересекаются, причем точки пересечения одноименных проекций таких прямых лежат на одной линии связи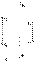 Задание плоскости тремя точками.
Задание плоскости тремя точками. 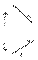 Задание плоскости прямой и точкой вне этой прямой.
Задание плоскости прямой и точкой вне этой прямой. 
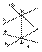 Задание плоскости двумя пересекающимися прямыми.
Задание плоскости двумя пересекающимися прямыми.  В ряде случаев плоскость удобно задавать двумя пересекающимися прямыми уровня: горизонталью и фронталью.
В ряде случаев плоскость удобно задавать двумя пересекающимися прямыми уровня: горизонталью и фронталью.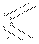 Задание плоскости двумя параллельными прямыми.
Задание плоскости двумя параллельными прямыми.  Задание плоскости плоской фигурой (отсек плоскости).
Задание плоскости плоской фигурой (отсек плоскости).  Пусть точка А (рис.2.12) равномерно движется по прямой 1, прямая, в свою очередь, равномерно вращается вокруг оси i, ей параллельной. При вращении прямая 1 образует цилиндрическую поверхность, а точка А опишет пространственную кривую, которую называют цилиндрической винтовой линией или гелисой (геликой). Расстояние от точки А до оси i называют радиусом винтовой линии, а расстояние между точками А1 и АVIII, лежащими на одной прямой - шагом винтовой линии.
Пусть точка А (рис.2.12) равномерно движется по прямой 1, прямая, в свою очередь, равномерно вращается вокруг оси i, ей параллельной. При вращении прямая 1 образует цилиндрическую поверхность, а точка А опишет пространственную кривую, которую называют цилиндрической винтовой линией или гелисой (геликой). Расстояние от точки А до оси i называют радиусом винтовой линии, а расстояние между точками А1 и АVIII, лежащими на одной прямой - шагом винтовой линии.
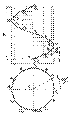 Построим комплексный чертеж винтовой линии по ее радиусу R и шагу р (рис.2.13). Примем ось винтовой линии i, расположенной перпендикулярно горизонтальной плоскости проекций П 1. Все точки винтовой линии отстоят от оси на одинаковом расстоянии, поэтому горизонтальной проекцией этой линии будет окружность радиуса R с центром на оси L. Выберем начальную точку винтовой линии - точку 1. Разделим окружность на 12 равных частей и примем полученные точки за горизонтальные проекции точек, принадлежащих винтовой линии. По условию задачи шаг винтовой линии равен р, следовательно, при переходе точки 1 в положение 2 она поднимется на высоту, равную 1/12 р, при переходе в положение 3 - на высоту 2/12 р и т.д. Поделив шаг на 12 частей, построим фронтальные проекции точек, принадлежащих винтовой линии.
Построим комплексный чертеж винтовой линии по ее радиусу R и шагу р (рис.2.13). Примем ось винтовой линии i, расположенной перпендикулярно горизонтальной плоскости проекций П 1. Все точки винтовой линии отстоят от оси на одинаковом расстоянии, поэтому горизонтальной проекцией этой линии будет окружность радиуса R с центром на оси L. Выберем начальную точку винтовой линии - точку 1. Разделим окружность на 12 равных частей и примем полученные точки за горизонтальные проекции точек, принадлежащих винтовой линии. По условию задачи шаг винтовой линии равен р, следовательно, при переходе точки 1 в положение 2 она поднимется на высоту, равную 1/12 р, при переходе в положение 3 - на высоту 2/12 р и т.д. Поделив шаг на 12 частей, построим фронтальные проекции точек, принадлежащих винтовой линии. 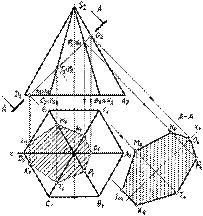 Сечение цилиндра.
Сечение цилиндра.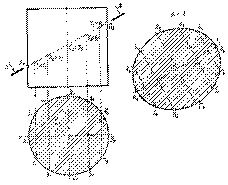
 Так как сечение шара - круг (рис. 8.7), то построение его натуральной величины сводится к определению радиуса окружности. Участок линии сечения А 3 В 3 является диаметром этой окружности. Поэтому для построений на новую ось х 1 линиями связи переносятся точки О и В, после чего радиусом, равным расстоянию между ними, проводится окружность - граница фигуры сечения А - А.
Так как сечение шара - круг (рис. 8.7), то построение его натуральной величины сводится к определению радиуса окружности. Участок линии сечения А 3 В 3 является диаметром этой окружности. Поэтому для построений на новую ось х 1 линиями связи переносятся точки О и В, после чего радиусом, равным расстоянию между ними, проводится окружность - граница фигуры сечения А - А.
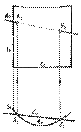 Построение точки встречи прямой общего положения с проецирующей поверхностью
Построение точки встречи прямой общего положения с проецирующей поверхностью 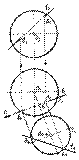 Построим точки встречи прямой 1 с поверхностью сферы. Заключим прямую 1 в горизонтально проецирующую плоскость Г (Г 1 º 1 1). Эта плоскость пересечет сферу по окружности, которая на плоскость П 2 спроецируется в эллипс с большой С 2 D 2 и малой Е 2 F 2 осями. В пересечении фронтальной проекции 1 2 прямой 1 с эллипсом получим А 2 и В 2 -фронтальные проекции искомых точек.
Построим точки встречи прямой 1 с поверхностью сферы. Заключим прямую 1 в горизонтально проецирующую плоскость Г (Г 1 º 1 1). Эта плоскость пересечет сферу по окружности, которая на плоскость П 2 спроецируется в эллипс с большой С 2 D 2 и малой Е 2 F 2 осями. В пересечении фронтальной проекции 1 2 прямой 1 с эллипсом получим А 2 и В 2 -фронтальные проекции искомых точек. 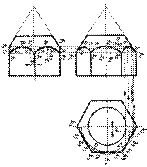

 Пример построения точек встречи горизонтальной прямой 1 с поверхностью тора.
Пример построения точек встречи горизонтальной прямой 1 с поверхностью тора.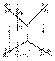 На рис.7.5 показано построение точки встречи горизонтально проецирующей прямой n с плоскостью общего положения Q (a Ç b). Горизонтальные проекции всех точек, принадлежащих данной прямой, в том числе и горизонтальная проекция М 1 искомой точки М, будут совпадать с n 1 - горизонтальной проекцией прямой n. Следовательно, задача сводится к нахождению недостающей фронтальной проекции М 1 точки М, лежащей в плоскости Q. Через М 1 проведем прямую 1 1 2 1. По линиям связи найдем фронтальные проекции 1 2, 2 2 точек 1 и 2, через которые проведем фронтальную проекцию прямой 12. На пересечении 1 2 2 2 с n 2 и будет находиться фронтальная проекция М 2 точки М.
На рис.7.5 показано построение точки встречи горизонтально проецирующей прямой n с плоскостью общего положения Q (a Ç b). Горизонтальные проекции всех точек, принадлежащих данной прямой, в том числе и горизонтальная проекция М 1 искомой точки М, будут совпадать с n 1 - горизонтальной проекцией прямой n. Следовательно, задача сводится к нахождению недостающей фронтальной проекции М 1 точки М, лежащей в плоскости Q. Через М 1 проведем прямую 1 1 2 1. По линиям связи найдем фронтальные проекции 1 2, 2 2 точек 1 и 2, через которые проведем фронтальную проекцию прямой 12. На пересечении 1 2 2 2 с n 2 и будет находиться фронтальная проекция М 2 точки М. прямой n, как точка, принадлежащая прямой n. В то же время фронтальная проекция М 2 точки М должна лежать на следе Q 2 плоскости Q, так как искомая точка принадлежит и плоскости Q. Следовательно, искомая фронтальная проекция М 2 точки М может лежать только на пересечении n 2 и Q 2. Имея фронтальную проекцию М 2 точки М, при помощи линии связи легко найти ее горизонтальную проекцию.
прямой n, как точка, принадлежащая прямой n. В то же время фронтальная проекция М 2 точки М должна лежать на следе Q 2 плоскости Q, так как искомая точка принадлежит и плоскости Q. Следовательно, искомая фронтальная проекция М 2 точки М может лежать только на пересечении n 2 и Q 2. Имея фронтальную проекцию М 2 точки М, при помощи линии связи легко найти ее горизонтальную проекцию. 3). Пересечение прямой общего положения с пл-тьюобщего положения.
3). Пересечение прямой общего положения с пл-тьюобщего положения.


