Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные законы алгебры логики:Содержание книги
Поиск на нашем сайте
Минимизация логических функций. Минимизация логических функций выполняется 1. с помощью законов алгебры логики 2. с помощью карт Карно (диаграмм Вейча) Метод алгебраической минимизации Метод заключается в использовании законов алгебры – логики. Суть метода: метод основан на последовательном исключении переменного исходного выражения с использованием алгебры-логики Минимизация с использованием карт Карно Карты Карно – специальная таблица, разбитая на клетки, каждая из которых соответствует 1 минтерну. Число клеток = числу различных наборов аргументов. Операция поглощения: Операция склеивания: Свертка для трех переменных: Карты для минимизации СДНФ представляют собой таблицу, разбитую на клетки, каждая из которых соответствует одному из возможных сочетаний переменных (минтермов, которые отличаются друг от друга одной переменной) Упрощение ниже. 1) представление переключательной функции на карте Карно. На карте нужно записать единицы в клетках, соответствующих заданным сочетаниям переменных, при которых функция равна единице. 2) объединение (склеивание) минтермов. В общем виде минтермы склеиваются в случаях: единицы соответствующих минтермов, количество которых кратно двум, расположены рядом в одном столбце (строке) или образуют квадрат; единицы соответствующих минтермов расположены в противоположных концах столбца (строки) или по противоположным углам. Нужно учитывать, что количество единиц в склейке должно быть максимальным. За счет этого минимизация становится оптимальной и не требует лишних действий. 3) получение результата минимизации. Для минтермов, охваченных оптимальной склейкой, выявляются общие переменные, которые и являются результатом упрощения. Комбинационные цифровые устройства. Порядок проведения синтеза комбинационных устройств. Пример синтеза кодопреобразователя из кода 8-4-2-1 в код 4-1-2-1. КЦУ – устройства, выходной сигнал которых полностью определяется комбинацией входных сигналов в данный момент времени. Такие устройства не обладают памятью. Порядок синтеза: - формализация правил работы комбинационного устройства. На основании общих требований к цифровому устройству составляются условия функционирования комбинационного устройства в виде таблицы истинности, структурных формул или совокупности номеров единичных (нулевых) наборов входных сигналов - минимизация структурных формул. В зависимости от конкретных условий при проведении этого этапа используется алгебраический или графический метод минимизации - запись минимизированных структурных формул в заданном базисе (И-НЕ, ИЛИ-НЕ) - составление структурной схемы. На основании структурной формулы каждой логической операции ставится в соответствие логический элемент выбранного базиса и осуществляются необходимые связи между элементами. Составление схемы начинается с определения необходимого числа инверторов, затем выявляются типы используемых логических элементов и, наконец, устанавливаются связи выход-вход согласно последовательности выполняемых логических операций Пример синтеза кодопреобразователя из кода 8-4-2-1 в код 4-1-2-1: - составление таблицы истинности: 8-4-2-1 |
4 - 1 - 2 -1 | ||||||||||
| N | X3 | X2 | X1 | X0 | Y3 | Y2 | Y1 | Y0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||||
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | ||||
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 4 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | ||||
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | ||||
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | ||||
| 7 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||||
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | ||||
| 9 | 1 | 0 | 0 | 1 | 3 | 3 | 3 | 3 | ||||
| 10 | 1 | 0 | 1 | 0 | 3 | 3 | 3 | 3 | ||||
| 11 | 1 | 0 | 1 | 1 | 3 | 3 | 3 | 3 | ||||
| 12 | 1 | 1 | 0 | 0 | 3 | 3 | 3 | 3 | ||||
| 13 | 1 | 1 | 0 | 1 | 3 | 3 | 3 | 3 | ||||
| 14 | 1 | 1 | 1 | 0 | 3 | 3 | 3 | 3 | ||||
| 15 | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 3 | ||||
- заполнение карт Карно:
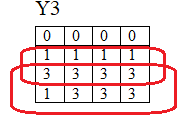
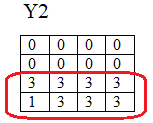
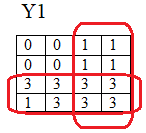
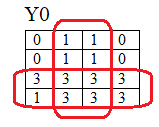
- запись полученных логических функций:
- Y3=X3+X2
- Y2=X3
- Y1=X3+X1
- Y0=X3+X0
- построение и проверка схемы кодопреобразователя (программа EWB):
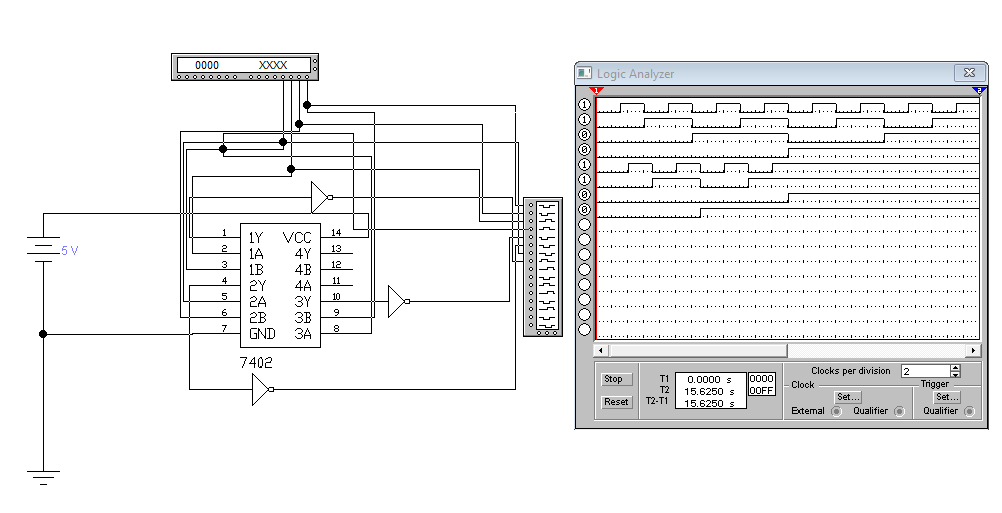
Шифраторы и дешифраторы. Примеры применения. Синтез линейного дешифратора 2Х4.
Шифратор - комбинационное устройство, преобразующее кодовую комбинацию в двоичную систему счисления, причем каждому входу может быть поставлена в соответствие кодовая комбинация, а набор выходных логических сигналов соответствует определенному двоичному коду. Если количество входов настолько велико, что в шифраторе используются все возможные комбинации сигналов на выходе, то такой шифратор называется полным, если не все, то неполным. Число входов и выходов в полном шифраторе связано соотношением n = 2m, где n— число входов, m— число выходов. Применения шифраторов: сокращение количества сигнальных линий, что очень удобно при передаче сигналов на большие расстояния, но при этом, входные сигналы не должны приходить одновременно на все входы. Наличие у шифратора дополнительных входных и выходных линий позволяет объединить их для увеличения разрядности шифратора, но только с помощью дополнительных логических элементов.
Дешифратор - комбинационное устройство с n входами и m выходами, преобразующее n-разрядный параллельный код, поступающий на входы, в логическую 1 на одном из выходов. Число входов и выходов в так называемом полном дешифраторе связано соотношением m = 2n, где n - число входов, а m - число выходов. Если в работе дешифратора используется неполное число выходов, то такой дешифратор называется неполным. Применения дешифраторов: непосредственно дешифрование входных кодов, селекция кодов (выбирает определенный код и выдает сигнал, что этот код получен), мультиплексирование.
Синтез линейного дешифратора 2х4 (2 входа и 4 выхода; линейный он потому, что основой такого дешифратора является линейка логических элементов):
- составление таблицы истинности:
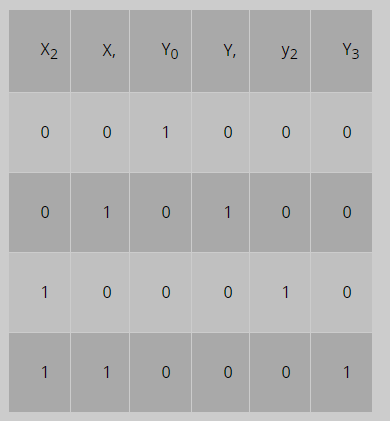
- составление функций, их минимизация и построение структурной схемы дешифратора:
|
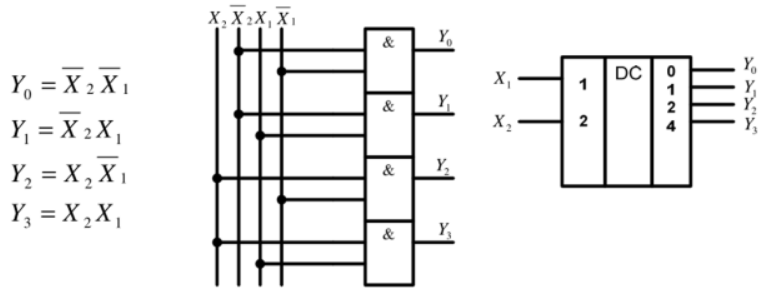
| Поделиться: |
