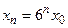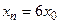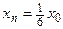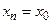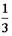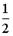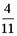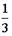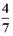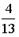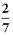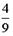Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие дифференциальные уравнения первого порядка с начальными условиямиСодержание книги
Поиск на нашем сайте
Простейшие дифференциальные уравнения первого порядка с начальными условиями
V1: «Разностные уравнения и их приложения» I: S: Порядок разностного уравнения -: 5; -: 4; +: 7; -: 6. I: S: Порядок разностного уравнения +: 5; -: 7; -: 4; -: 6. I: S: Характеристическое уравнение соответствующее разностному уравнению +: 4,-1; -: -4, -1; -: -4, 1; -: 4, 1. I: S: Характеристическое уравнение соответствующее разностному уравнению +: 2, -5; -: -2, -5; -: 2, 5; -: -2, 5. I: S: Характеристическое уравнение соответствующее разностному уравнению -: -: +: -: I: S: Характеристическое уравнение соответствующее разностному уравнению -: -: -: +: I: S: Общее решение разностного уравнения -: +: -: -: I: S: Общее решение разностного уравнения +: -: -: -: I: S: Разностное уравнение -: линейным и неоднородным +: нелинейным и неоднородным -: линейным и однородным -: нелинейным и однородным I: S: Разностное уравнение -: линейным и неоднородным -: нелинейным и неоднородным -: линейным и однородным +: нелинейным и однородным I: S: Разностное уравнение -: линейным и неоднородным -: нелинейным и неоднородным -: линейным и однородным +: нелинейным и однородным I: S: Разностное уравнение -: линейным и неоднородным +: нелинейным и неоднородным -: линейным и однородным -: нелинейным и однородным
I: S: Решение разностного уравнения -: +: -: -: I: S: Решение разностного уравнения +: -: -: -: V1: «Классическое определение вероятности» I: S: Игральный кубик бросают один раз. Событие А – «Выпало число очков большее, чем 3». Событие В – «Выпало число очков меньшее, чем 3». Тогда для этих событий верным будет утверждение: -: «Событие А достоверно» +: «События А и В несовместны» -: «События А и В совместны» -: «Событие В достоверно» I: S: В урне 10 черных шаров. Опыт состоит в выборе только одного шара. Событие А – «Вынули белый шар». Событие В – «Вынули черный шар». Тогда для этих событий верным будет утверждение: -: «Вероятность события А равна 0» +: «Событие В достоверно» -: «События А и В равновероятны» -: «Событие А достоверно» I: S: В ящике 5 качественных и 5 бракованных изделий. Опыт состоит в выборе только одного изделия. Событие А – «Вынули качественное изделие». Событие В – «Вынули бракованное изделие». Тогда для этих событий верным будет утверждение: +: «События А и В равновероятны» -: «Событие А достоверно» -: «Событие В невозможно» -: «Вероятность события В больше вероятности события А» I: S: Вероятность наступления некоторого события не может быть равна... -: 0,8 -: 0,9 -: 1 +: 1,1 I: S: Из урны, в которой находятся 6 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна… +: -: 1 -: -: I: S: Из урны, в которой находятся 4 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна… -: -: 1 +: -: I: S: Из урны, в которой находятся 4 белых и 5 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет черным, равна… -: -: 1 -: +: I: S: Из урны, в которой находятся 5 белых и 3 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет черным, равна… -: -: 1 -: +: I: S: Футбольная команда выиграет первый матч с вероятностью 0,3, а второй – с вероятностью 0,4. Тогда вероятность того, что команда выиграет оба матча, равна … -: 1,1 -: 0,4 -: 0,7 +: 0,12 I: S: Студент Иванов придет на лекцию с вероятностью 0,8, а студент Петров – с вероятностью 0,6. Тогда вероятность того, что оба студента будут на лекции, равна …
+: 0,48 -: 1,4 -: 0,8 -: 0,6 I: S: Белый шар из первой урны можно вытащить с вероятностью 0,3; из второй – с вероятностью 0,9. Вытащили по одному шару из каждой урны. Тогда вероятность вытащить два белых шара равна … -: 0,9 -: 0,3 -: 1,2 +: 0,45 I: S: Два одноклассника поступают в институт на разные факультеты. Первый одноклассник поступит с вероятностью 0,4; второй – с вероятностью 0,7. Тогда вероятность того, что оба одноклассника поступят, равна … -: 0,8 +: 0,28 -: 1,1 -: 0,3 I: S: Дан закон распределения вероятностей дискретной случайной величины
Тогда значение a равно… +: 0, 5 -: 0, 6 -: 0, 8 +: 0,4 I: S: Дан закон распределения вероятностей дискретной случайной величины
Тогда значение a равно… +: 0,6 -: 0,5 -: 0,7 -: 0,8 I: S: Дан закон распределения вероятностей дискретной случайной величины
+: 0,5 -: 0,6 -: -0,4 -: 0,3 I: S: Дан закон распределения вероятностей дискретной случайной величины
Тогда значение a равно… +: 0,1 -: 0,2 -: 0,3 -: 0, 5 I: S: Дан закон распределения вероятностей дискретной случайной величины
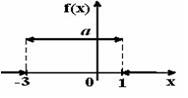
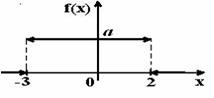
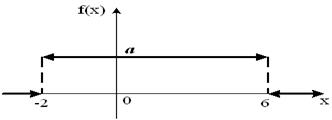
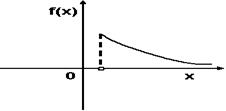
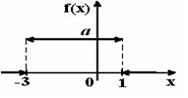
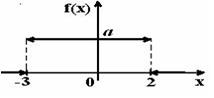
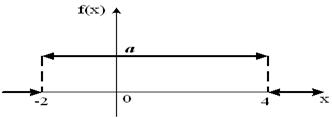
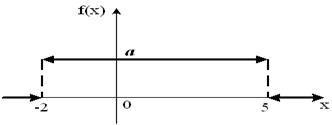
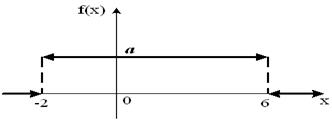
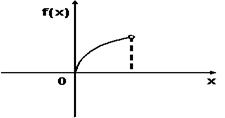
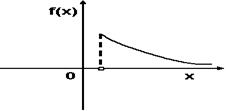
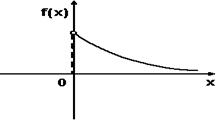
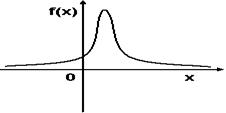
Тогда значение a равно… +: 0,6 -: 0,7 -: -0,8 -: 0,5 V1:«Законы распределения вероятностей непрерывных случайных величин I: S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид: +: 0,25 -: 1 -: 0,33 -: 0,2 I: S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид: +: 0,25 -: 1 -: 0,4 -: 0,2 I: S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид: +: 0,2 -: 1 -: 0,25 -: 0,4 I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности вероятностей для нормального распределения изображен на рисунке... -: -: -: +: I: S: Решение разностного уравнения -: +: -: -: I: S: Решение разностного уравнения +: -: -: -: S: В ящике 5 качественных и 5 бракованных изделий. Опыт состоит в выборе только одного изделия. Событие А – «Вынули качественное изделие». Событие В – «Вынули бракованное изделие». Тогда для этих событий верным будет утверждение: +: «События А и В равновероятны» -: «Событие А достоверно» -: «Событие В невозможно» -: «Вероятность события В больше вероятности события А»
I: S: Вероятность наступления некоторого события не может быть равна... -: 0,9 -: 0,99 -: 1 +: 1,2 I: S: Из урны, в которой находятся 5 белых и 10 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна… +: -: 1 -: -: I: S: Из урны, в которой находятся 3 белых и 6 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна… -: -: 1 +: -: I: S: Из урны, в которой находятся 4 белых и 5 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна… -: -: 1 -: +: I: S: Из урны, в которой находятся 5 белых и 3 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна… -: -: 1 -: +: I: S: Футбольная команда выиграет первый матч с вероятностью 0,6, а второй – с вероятностью 0,5. Тогда вероятность того, что команда выиграет оба матча, равна … -: 1,1 -: 0,6 -: 0,5 +: 0,3 I: S: Студент Иванов придет на лекцию с вероятностью 0,3, а студент Петров – с вероятностью 0,7. Тогда вероятность того, что оба студента будут на лекции, равна … +: 0,21 -: 1 -: 0,4 -: 0,7 I: S: Белый шар из первой урны можно вытащить с вероятностью 0,5; из второй – с вероятностью 0,7. Вытащили по одному шару из каждой урны. Тогда вероятность вытащить два белых шара равна … -: 0,5 -: 0,2 -: 1,2 +: 0,35 I: S: Два одноклассника поступают в институт на разные факультеты. Первый одноклассник поступит с вероятностью 0,6; второй – с вероятностью 0,8. Тогда вероятность того, что оба одноклассника поступят, равна … -: 0,8 +: 0,48 -: 1,4 -: 0,2 I: S: Дан закон распределения вероятностей дискретной случайной величины
Тогда значение a равно… +: 0, 5 -: 0, 6 -: 0, 8 -: 0,4 I: S: Дан закон распределения вероятностей дискретной случайной величины
Тогда значение a равно… +: 0,2 -: 0,1 -: 0,3 -: 0,22 I: S: Дан закон распределения вероятностей дискретной случайной величины
+: 0, 4 -: 0, 5 -: -0,4 -: 0,3 I: S: Дан закон распределения вероятностей дискретной случайной величины
Тогда значение a равно… +: 0, 7 -: 0, 8 -: 0,6 -: 0, 5 I: S: Дан закон распределения вероятностей дискретной случайной величины
Тогда значение a равно… +: 0,1 -: 0,2 -: -0,1 -: 0,3 V1:«Законы распределения вероятностей непрерывных случайных величин I: S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
+: 0,25 -: 1 -: 0,33 -: 0,2 I: S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид: +: 0,25 -: 1 -: 0,4 -: 0,2 I: S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид: +: 0,2 -: 1 -: 0,25 -: 0,4 I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид: +: -: 1 -: -: I: S: График плотности вероятностей для нормального распределения изображен на рисунке... -: -: -: +: 1) Частота колебаний в уравнении х=0.5 soc2п T 1 Увеличится в 2 раза 4) Циклическая (круговая) частота в уравнении х=0,5 cos2п t равна П Не измениться Магнитное поле создается Излучение лазера Когерентно Уменьшится в 9 раз Амперметр последовательно Реостатом Милливольтметром
Интерференцией 15) Во сколько примерно раз масса атома больше массы его ядра? Сила Лоренца Магнитное поле создается Дифракционной решеткой 21) в ядре изотопа урана 235\92 U содержится Нуклона Ареометром Электромагнитная индукция Протон Миллиамперметром Атомное ядро состоит из Протонов и нейтронов Частоты колебаний одинаковы 34) В ядре атома изотопа лития содержится Нейтрона 144 Прямая Свободных электронов Электронов С Только вольтметр Фиолетового цвета Электродвижущая сила Микровольтметром Дисперсией Интерференции света 10000 Менее оптической Зеркал Френеля Индуктивности 58) Как называется единица магнитной индукции? Тесла 59) если у тела количество протонов больше количества электронов то оно Положительно заряжено Больше скорость электрона Проводники отталкиваются
Более оптически плотной См 64) К электрическое поле напряженностью 200 Н\Кл внесли заряд 10-7 Кл. Определите силу, действующую на заряд Н br Фотоэффекта 66) Циклическая (круговая) частота в уравнении х= 0.5 soc2п T равна 2п Увеличится в 2 раза Корень из 3/2 Корень из 3 70) Период колебаний в уравнении х=0.5 cos2п t равен 1 Амперметра 0,5 С С Е1-Е2 См Микроамперметром
F1: Физика (ЛД, СТ) F2: Кумыков В.К. V1: ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ I: S: Гармоническими называются колебания: -: которые возникают в системе при участии внешней силы -: при которых их амплитуда под действием силы трения постепенно уменьшается +: при которых колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса -: при которых механические возмущения распространяются в пространстве и переносят энергию -: при которых их скорость остается постоянной I: S: Примером гармонических колебаний могут служить: +: колебания математического маятника -: колебания физического маятника -: периодические подскакивания в реальных условиях мяча, упавшего на землю -: круги, расходящиеся на поверхности воды от брошенного камня -: колебания температуры окружающей среды I: S: Фаза колебаний представляет собой: -: величину, численно равную времени, в течение которого совершается одно полное колебание -: величину, численно равную наибольшему отклонению колеблющегося тела от положения равновесия -: величину, численно равную числу колебаний за единицу времени +: величину, характеризующую положение колеблющейся точки в данный момент времени -: величину скорости распространения колебаний в данный момент времени I: S:Уравнение гармонических колебаний было получено в предположении: +: малости отклонения маятника от положения равновесия -: наличия вынуждающей силы, действующей на маятник -: отсутствия начальной фазы колебания : равенства нулю кинетической энергии маятника в положении равновесия -: наличия силы трения в точке подвеса маятника S:В выражении для смещения материальной точки X = А0 sin(ω0 t +...) в случае гармонических колебаний пропущен символ: +: -: -: -: -: I: S: Гармонические колебания описываются уравнением: +: |

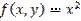 ,
, 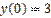 является:
является: 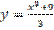
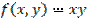 ,
, 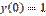 является:
является: 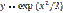
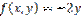 ,
, 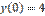 является:
является: 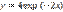
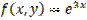 ,
, 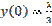 является:
является: 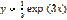
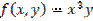 ,
, 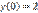 является:
является: 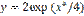
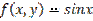 ,
, 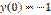 является:
является: 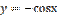
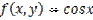 ,
, 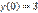 является:
является: 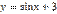
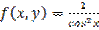 ,
, 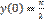 является:
является: 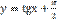
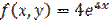 ,
, 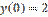 является:
является: 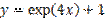
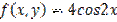 ,
, 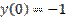 является:
является: 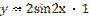
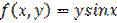 ,
, 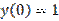 является:
является: 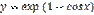
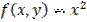 +1,
+1, 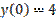 является:
является: 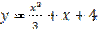
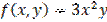 ,
, 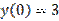 является:
является: 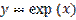
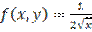 ,
, 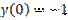 является:
является: 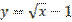
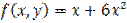 ,
, 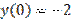 является:
является: 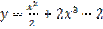
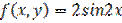 ,
, 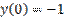 является:
является: 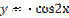
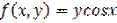 ,
, 
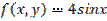 ,
, 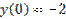 является:
является: 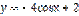
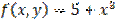 ,
, 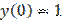 является:
является: 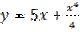
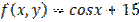 ,
, 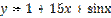
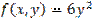 ,
, 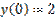 является:
является: 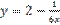
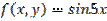 ,
, 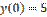 является:
является: 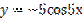
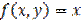 ,
, 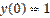 является:
является: 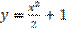
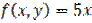 ,
, 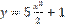
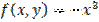 ,
, 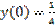 является:
является: 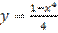
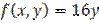 ,
, 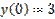 является:
является: 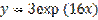
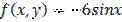 ,
, 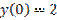 является:
является: 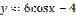
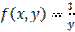 ,
, 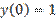 является:
является: 
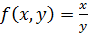 ,
, 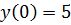 является:
является: 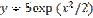
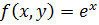 ,
, 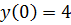 является:
является: 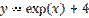
 ,
, 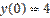 является:
является: 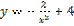
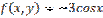 ,
, 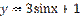
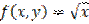 ,
, 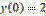 является:
является: 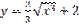
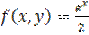 ,
, 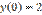 является:
является: 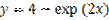
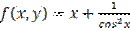 ,
, 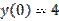 является:
является: 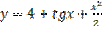
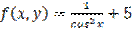 ,
, 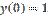 является:
является: 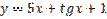
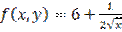 ,
, 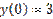 является:
является: 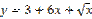
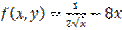 ,
, 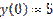 является:
является: 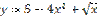
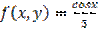 ,
, 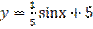
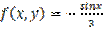 ,
, 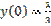 является:
является: 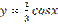
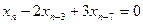 равен …
равен …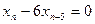 равен …
равен …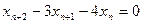 имеет корни
имеет корни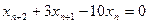 имеет корни
имеет корни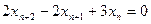 имеет вид
имеет вид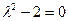
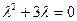
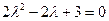
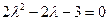
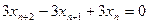 имеет вид
имеет вид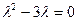
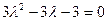
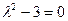
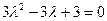
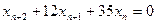 имеет вид
имеет вид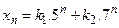
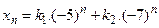
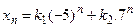
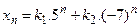
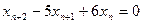 имеет вид
имеет вид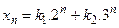
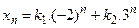
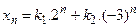
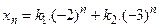
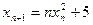 является
является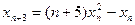 является
является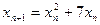 является
является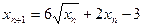 является
является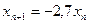 с начальным условием
с начальным условием 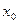 имеет вид
имеет вид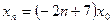
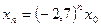
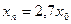
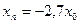
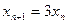 с начальным условием
с начальным условием 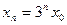
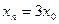
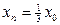
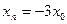
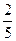
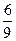
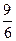
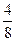
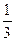
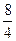
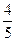
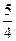
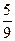
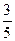
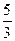
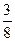
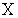 :
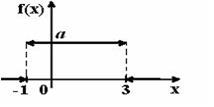
:

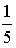

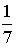

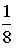
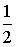
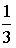
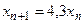 с начальным условием
с начальным условием 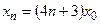
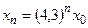
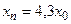
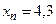
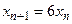 с начальным условием
с начальным условием