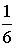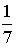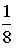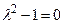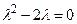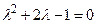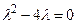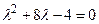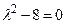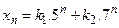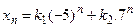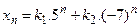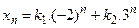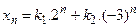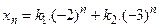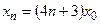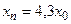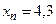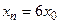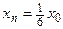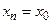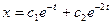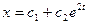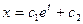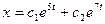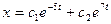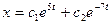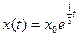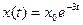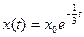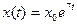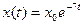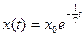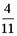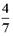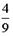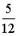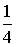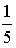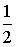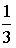Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
S: ток в электролитах обусловлен упорядоченным движением
-: Положительных ионов
+: Отрицательных ионов
-: Свободных электронов
-: Нейтральных атомов
-: Свободных нейтронов
-: Свободных протонов
- «Разностные уравнения и их приложения – 14 вопросов»
- Порядок разностного уравнения
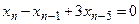 равен …5; равен …5; - Порядок разностного уравнения
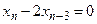 равен …3; равен …3; - Характеристическое уравнение соответствующее разностному уравнению
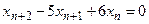 имеет корни +: 2, 3; имеет корни +: 2, 3; - Характеристическое уравнение соответствующее разностному уравнению
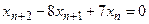 имеет корни 1, 7; имеет корни 1, 7; - Характеристическое уравнение соответствующее разностному уравнению
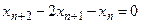 имеет вид имеет вид 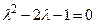 - Характеристическое уравнение соответствующее разностному уравнению
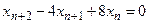 имеет вид имеет вид 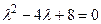 - Общее решение разностного уравнения
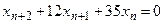 имеет вид имеет вид 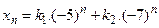
· Общее решение разностного уравнения 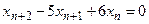 имеет вид имеет вид
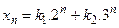
· Разностное уравнение 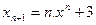 является линейным и неоднородным является линейным и неоднородным
· Разностное уравнение 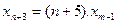 является линейным и однородным является линейным и однородным
· Разностное уравнение 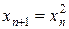 является нелинейным и однородным является нелинейным и однородным
· Разностное уравнение 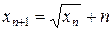 является нелинейным и неоднородным является нелинейным и неоднородным
· Решение разностного уравнения 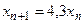 с начальным условием с начальным условием 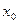 имеет вид имеет вид 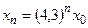
· Решение разностного уравнения 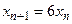 с начальным условием с начальным условием 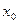 имеет вид имеет вид 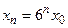
«Дифференциальные уравнения и их приложения в биологии»
- Дифференциальное уравнение
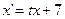 является линейным и неоднородным является линейным и неоднородным - Дифференциальное уравнение
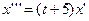 является линейным и однородным является линейным и однородным - Дифференциальное уравнение
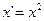 является нелинейным и однородным является нелинейным и однородным - Дифференциальное уравнение
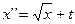 является нелинейным и неоднородным является нелинейным и неоднородным - S: Общее решение дифференциального уравнения
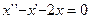 имеет вид имеет вид 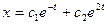
- Общее решение дифференциального уравнения
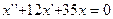 имеет вид имеет вид 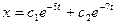
- Порядок дифференциального уравнения
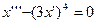 равен 3 равен 3 - S: Порядок дифференциального уравнения
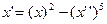 равен 2 равен 2 - S: Решение дифференциального уравнения
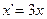 с начальным условием с начальным условием 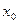 имеет вид имеет вид 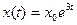
- Решение дифференциального уравнения
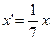 с начальным условием с начальным условием 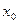 имеет вид имеет вид 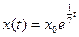
«Классическое определение вероятности»
- Игральный кубик бросают один раз. Событие А – «Выпало число очков большее, чем 3». Событие В – «Выпало число очков меньшее, чем 3». Тогда для этих событий верным будет утверждение: «События А и В несовместны»
- В урне 10 белых шаров. Опыт состоит в выборе только одного шара. Событие А – «Вынули белый шар». Событие В – «Вынули черный шар». Тогда для этих событий верным будет утверждение: «Событие А достоверно»
- В ящике 5 качественных и 5 бракованных изделий. Опыт состоит в выборе только одного изделия. Событие А – «Вынули качественное изделие». Событие В – «Вынули бракованное изделие». Тогда для этих событий верным будет утверждение: «События А и В равновероятны»
- Вероятность наступления некоторого события не может быть равна... 1,3
- Из урны, в которой находятся 4 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
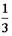 - Из урны, в которой находятся 4 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
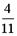 - S: Из урны, в которой находятся 4 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
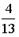
- S: Из урны, в которой находятся 5 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
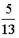 «Теоремы сложения и умножения вероятностей. Формула полной вероятности»
- S: Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна… 0,2
- Футбольная команда выиграет первый матч с вероятностью 0,9, а второй – с вероятностью 0,4. Тогда вероятность того, что команда выиграет оба матча, равна 0,36
- S: Студент Иванов придет на лекцию с вероятностью 0,2, а студент Петров – с вероятностью 0,8. Тогда вероятность того, что оба студента будут на лекции, равна …
0,16
- Белый шар из первой урны можно вытащить с вероятностью 0,2; из второй – с вероятностью 0,7. Вытащили по одному шару из каждой урны. Тогда вероятность вытащить два белых шара равна … 0,14
- Два одноклассника поступают в институт на разные факультеты. Первый одноклассник поступит с вероятностью 0,5; второй – с вероятностью 0,6. Тогда вероятность того, что оба одноклассника поступят, равна …0,3
- В первой урне 4 белых и 6 черных шаров. Во второй урне 1 белый и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,25
- В первой урне 2 черных и 8 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,55
- В первой урне 1 черный и 9 белых шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,65
- В первой урне 5 белых и 5 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,6
- В первой урне 2 белых и 8 черных шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна… 0,25
«Числовые характеристики дискретных случайных величин»
- Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
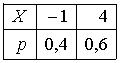
Тогда математическое ожидание этой случайной величины равно…2 - Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
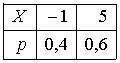
Тогда математическое ожидание этой случайной величины равно…2,6 - Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
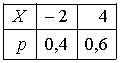
Тогда математическое ожидание этой случайной величины равно…1,6 - Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
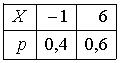
Тогда математическое ожидание этой случайной величины равно…3,2 - Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:
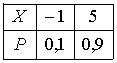
Тогда математическое ожидание этой случайной величины равно…4,4 - Дан закон распределения вероятностей дискретной случайной величины
 : :
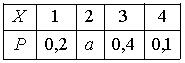
Тогда значение a равно… 0,3 - Дан закон распределения вероятностей дискретной случайной величины
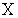 : :
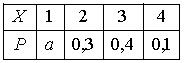
Тогда значение a равно… 0,2 - Дан закон распределения вероятностей дискретной случайной величины
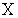 : :
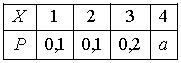
Тогда значение a равно… 0,6 - Дан закон распределения вероятностей дискретной случайной величины
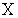 : :
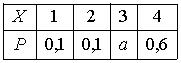
Тогда значение a равно… 0,2 - Дан закон распределения вероятностей дискретной случайной величины
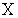 : :
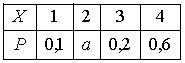
Тогда значение a равно… 0,1 «Законы распределения вероятностей непрерывных случайных величин -10 вопросов»
- График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
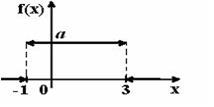
Тогда значение а равно… 0,25 - График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
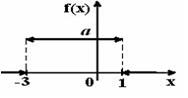
Тогда значение а равно… 0,25 - График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
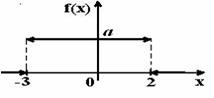
Тогда значение а равно… 0,2 - График плотности распределения вероятностей непрерывной случайной величины X имеет вид:

Тогда значение a равно…  - График плотности распределения вероятностей непрерывной случайной величины X имеет вид:

Тогда значение a равно…  - График плотности распределения вероятностей непрерывной случайной величины X имеет вид:

Тогда значение a равно…  - График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
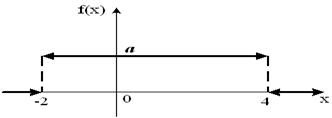
Тогда значение a равно… 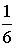 - График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
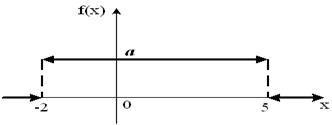
Тогда значение a равно… 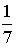 - График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
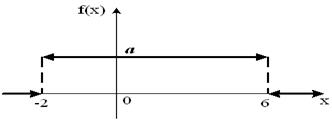
Тогда значение a равно… 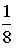
- График плотности вероятностей для нормального распределения изображен на рисунке...
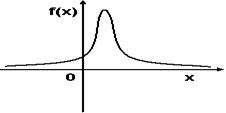
ФИЗИКА
- Амплитудой колебаний называется: величина,численно равная наибольшему отклонению движущегося тела от положения равновесия
- Атмосферное давление измеряется: барометром
- Атомы в рамках Резерфордовского представления представляют собой: положительный заряд сосредоточен в центре, а электроны вращаются вокруг
- В формуле T=2П корень l/g описывается колебание: математического маятника.
- В формуле T=2П корень m/k описывается колебание: пружинного маятника.
- В формуле гармонических колебаний А представляет: амплитуду
- В формуле гармонических колебаний Х: смещение.
- В явлении интерференции обнаруживаются свойства: волновые
- Величина “Фи”0: начальная фаза
- Величина напряженности магнитного поля определяется как: отношение силы, с которой поле действует на единичный … тока, располагающийся перпендикулярно нулю.
- Влажность воздуха определяется: гигрометром и психрометром
- Восприимчивость вещества к намагничиванию под действием внешнего магнитного поля,называется: магнитной проницаемостью
- Вязкость жидкости определяется: искозиметром
- Гальванометр: регулируется на весьма малые силы тока
- Гармонические колебания описываются уравнением: x=Acos(wt+ф)
- Гармоническими называются колебания: при которой колеблюющаяся величина изменяются в зависимости от времени по закону синуса или косинуса
- Дифракцией света называется: отклонение света от прямолинейного распределения в среде с разными неоднородн.
- Дифракционная решетка используется для: получения дифракционных спектров
- Дифракция света это: отклонение света от прямолинейности распространения в среде с резкими неравномерностями
- Для измерения плотности потоков ионизирующих излучений используется: радиометр
- Для магнитного поля непрерываемого прямолинейным проводником с током справедлива формула Ампера: dF=мю0I0dl0dH
- Для определения величины напряженности магнитного поля в проводниках с током следует использовать выражение: dH=Idlsin”альфа”/ 4”пи”r2
- Для определения концентрации веществ в контрастных (окрашенных) растворах используется: калориметр
- Единицей измерения потенциала является: В
- Единицей измерения силы электрического поля является: А
- Единицей измерения сопротивления электрического поля является: Ом
- Единицой измерения напряженности электрического поля является: В|м
- Закон Ома для участка цепи: I=U|R
- Измерение давления газов или жидкостей проводится: монометром
- Индукция магнитного поля измеряется в: Тл
- Интерференцией света называется явление: получение световых пучков от когерентных нейтронов.
- Когерентными называются волны которые излучаются: из одного источника
- Когерентными называются источники, которые излучают: с постоянной разностью фаз.
- Математическим выражением третьего постулата Бора это: H “нью”= dB1/dB2, здесь H “нью” ватт энергии, а dB1/dB2 энергия соответственно начальная и конечная
- Модель атома Резерфорда была усовершенствована: Бором
- Направление силы Ампера определяется: по закону левой руки
- Напряженность магнитного поля измеряется в: А|м
- Напряженность поля является его: силовой характеристикой
- Напряженность электрического поля измеряется в: вольт/метр
- Напряженность электрического поля определяется выражением: E=F|q
- Недостатки Резерфордовской модели атома: в резерфордовской модели атом является неустойчивым образованием
- Неподвижные электрические заряды взаимодействуют по закону: Кулона
- Определение концентрации сахара в растворах производится: паляриметром
- Освещенность измеряют: люксметром
- Периодом колебаний называется: величина,численно равная времени за которое совершается одно полное колебание
- Плотность жидкости определяется: ареометром
- Поверхностное натяжение жидкости определяется: сталагмометром
- Показатель преломления света определяется: рефрактометром
- Потенциал измеряется в: вольт
- Потенциал электрического поля определяется выражением: Ф=A|q
- Потенциал электрического поля определяется выражением: “Фи” =a/q, здесь фи это потенциал электрического поля
- Потенциал электрического поля является его: энергетической характеристикой
- Поток магнитной индукции измеряется в: Вб
- Прибор в котором при облучении поверности металлов светом возникает фотоэффект: фотоэлементом
- Прибор для измерения активной электрической мощности: ваттметр
- Прибор для измерения различных электрический величин наз: осциллографом
- Прибор для регулирования силы тока и напряжения: реостат Прибор для наблюдения и измерения периферических величин называется: осциллограф Электрическое напряжение в цепи измеряется: вольтметром
- Примером гармонических колебаний могут быть: колебания математического маятника
- Сила взаимодействия неподвижных электрических зарядов определяется выражением: F=kq1q2/r в квадрате
- Сила переменного тока изменяется по закону: синуса,косинуса
- Сила перемещения тока измеряется по закону E=… /Mt
- Сила тока определяется выражением: I=q|t
- Сила электрического тока в цепи измеряется: амперметром
- Согласно первому постулату Бора: электроны могут двигаться не по любым орбитам, а по орбитам вполне определенным
- Согласно постулату Бора: движение электронов по стационарным орбитам не сопровождается излучением
- Согласно постулату Бора: переход электрона с одной стационарной орбиты на другую, сопровождается поглощением или излучением
- Сопротивление проводника цилиндрической формы определяется выражением: R=”ро”l|s
- Центростремительной силой удерживающей электроны в орбите является: кулоновская сила
- Частотой колебаний называется: величина,численно равная числу колебаний за единицу времени
- Электрический ток в металлах определяется упорядоченным движением: электронов
- Электромагнитное устройство преобр. параллельный ток одного напряжения и первый ток другого напряжения наз: трансформатором
- Элементарными заряженными частицами являются: электроны и протоны (или просто протоны)
- Эффективное “И”э и амплитуда “И”0 значение переменного тока соответственно: Иэ= И0/корень из 2
- Явление дифракции выявляет свойства: волновые
- Явление дифракции используется в: дифракционных решетках
- Явление интерференции используется: в интерфераметрах
- Явление интерференции используется в: интерферометрах
- Тестовые задания по теме «Разностные уравнения и их приложения – 14 вопросов»
- I:
- S: Порядок разностного уравнения
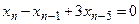 равен … равен … - +: 5;
- -: 4;
- -: 3;
- -: 6.
- I:
- S: Порядок разностного уравнения
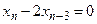 равен … равен … - -: 1;
- -: 2;
- +: 3;
- -: 4.
- I:
- S: Характеристическое уравнение соответствующее разностному уравнению
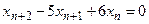 имеет корни имеет корни - -: 5, 6;
- -: 4, 2;
- +: 2, 3;
- -: 3, 4.
- I:
- S: Характеристическое уравнение соответствующее разностному уравнению
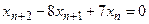 имеет корни имеет корни - +: 1, 7;
- -: 1, 3;
- -: 2, 4;
- -: -2, 4.
- I:
- S: Характеристическое уравнение соответствующее разностному уравнению
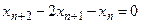 имеет вид имеет вид - -:
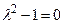 - -:
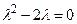 - +:
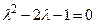 - -:
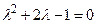 - I:
- S: Характеристическое уравнение соответствующее разностному уравнению
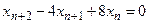 имеет вид имеет вид - -:
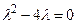 - -:
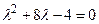 - -:
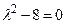 - +:
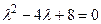 - I:
- S: Общее решение разностного уравнения
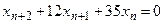 имеет вид имеет вид - -:
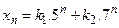 - +:
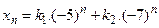 - -:
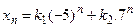 - -:
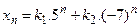 - I:
- S: Общее решение разностного уравнения
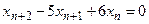 имеет вид имеет вид - +:
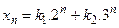 - -:
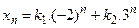 - -:
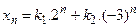 - -:
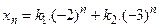 - I:
- S: Разностное уравнение
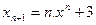 является является - +: линейным и неоднородным
- -: нелинейным и неоднородным
- -: линейным и однородным
- -: нелинейным и однородным
- I:
- S: Разностное уравнение
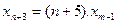 является является - -: линейным и неоднородным
- -: нелинейным и неоднородным
- +: линейным и однородным
- -: нелинейным и однородным
- I:
- S: Разностное уравнение
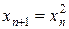 является является - -: линейным и неоднородным
- -: нелинейным и неоднородным
- -: линейным и однородным
- +: нелинейным и однородным
- I:
- S: Разностное уравнение
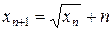 является является - -: линейным и неоднородным
- +: нелинейным и неоднородным
- -: линейным и однородным
- -: нелинейным и однородным
- I:
- S: Решение разностного уравнения
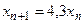 с начальным условием с начальным условием 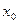 имеет вид имеет вид 153. -: 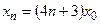
154. +: 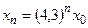
155. -: 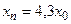
156. -: 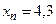
- I:
- S: Решение разностного уравнения
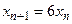 с начальным условием с начальным условием 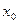 имеет вид имеет вид 159. +: 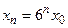
160. -: 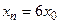
161. -: 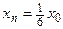
162. -: 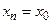
163.
- Тестовые задания по теме «Дифференциальные уравнения и их приложения в биологии – 10 вопросов»
- I:
- S: Дифференциальное уравнение
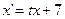 является является - +: линейным и неоднородным
- -: нелинейным и неоднородным
- -: линейным и однородным
- -: нелинейным и однородным
-
- I:
- S: Дифференциальное уравнение
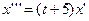 является является - -: линейным и неоднородным
- -: нелинейным и неоднородным
- +: линейным и однородным
- -: нелинейным и однородным
- I:
- S: Дифференциальное уравнение
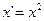 является является - -: линейным и неоднородным
- -: нелинейным и неоднородным
- -: линейным и однородным
- +: нелинейным и однородным
- I:
- S: Дифференциальное уравнение
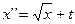 является является - -: линейным и неоднородным
- +: нелинейным и неоднородным
- -: линейным и однородным
- -: нелинейным и однородным
- I:
- S: Общее решение дифференциального уравнения
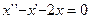 имеет вид имеет вид - +:
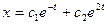 - -:
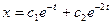 - -:
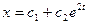 - -:
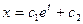 -
- I:
- S: Общее решение дифференциального уравнения
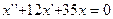 имеет вид имеет вид - -:
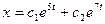 - +:
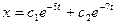 - -:
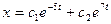 - -:
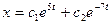 - I:
- S: Порядок дифференциального уравнения
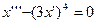 равен равен - -: 1
- -: 2
- +: 3
- -: 4
- I:
- S: Порядок дифференциального уравнения
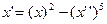 равен равен - -: 1
- +: 2
- -: 3
- -: 4
- I:
- S: Решение дифференциального уравнения
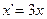 с начальным условием с начальным условием 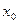 имеет вид имеет вид - +:
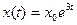 - -:
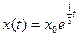 - -:
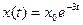 - -:
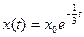 - I:
- S: Решение дифференциального уравнения
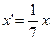 с начальным условием с начальным условием 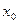 имеет вид имеет вид - -:
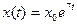 - +:
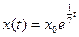 - -:
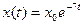 - -:
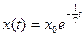 -
- Тестовые задания по теме «Классическое определение вероятности – 8 вопросов»
- I:
- S: Игральный кубик бросают один раз. Событие А – «Выпало число очков большее, чем 3». Событие В – «Выпало число очков меньшее, чем 3». Тогда для этих событий верным будет утверждение:
- -: «Событие А достоверно»
- +: «События А и В несовместны»
- -: «События А и В совместны»
- -: «Событие В достоверно»
- I:
- S: В урне 10 белых шаров. Опыт состоит в выборе только одного шара. Событие А – «Вынули белый шар». Событие В – «Вынули черный шар». Тогда для этих событий верным будет утверждение:
- -: «Вероятность события А равна 0»
- -: «Событие В достоверно»
- -: «События А и В равновероятны»
- +: «Событие А достоверно»
- I:
- S: В ящике 5 качественных и 5 бракованных изделий. Опыт состоит в выборе только одного изделия. Событие А – «Вынули качественное изделие». Событие В – «Вынули бракованное изделие». Тогда для этих событий верным будет утверждение:
- +: «События А и В равновероятны»
- -: «Событие А достоверно»
- -: «Событие В невозможно»
- -: «Вероятность события В больше вероятности события А»
- I:
- S: Вероятность наступления некоторого события не может быть равна...
- -: 0,7
- -: 0,3
- -: 1
- +: 1,3
- I:
- S: Из урны, в которой находятся 4 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
- +:
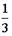 - -: 1
- -:
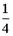 - -:
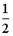 - I:
- S: Из урны, в которой находятся 4 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
- +:
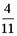 - -: 1
- -:
 - -:
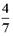 - I:
- S: Из урны, в которой находятся 4 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
- +:
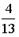 - -: 1
- -:
 - -:
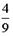 - I:
- S: Из урны, в которой находятся 5 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
- +:
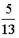 - -: 1
- -:
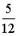 - -:
 - Тестовые задания по теме «Теоремы сложения и умножения вероятностей. Формула полной вероятности -10 вопросов»
- I:
- S: Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
- +: 0,2
- -: 0,9
- -: 0,16
- -: 0,3
- I:
- S: Футбольная команда выиграет первый матч с вероятностью 0,9, а второй – с вероятностью 0,4. Тогда вероятность того, что команда выиграет оба матча, равна …
- -: 1,3
- -: 0,5
- -: 0,64
- +: 0,36
- I:
- S: Студент Иванов придет на лекцию с вероятностью 0,2, а студент Петров – с вероятностью 0,8. Тогда вероятность того, что оба студента будут на лекции, равна …
- +: 0,16
- -: 0,6
- -: 0,84
- -: 1
- I:
- S: Белый шар из первой урны можно вытащить с вероятностью 0,2; из второй – с вероятностью 0,7. Вытащили по одному шару из каждой урны. Тогда вероятность вытащить два белых шара равна …
- -: 0,9
- -: 0,86
- -: 1
- +: 0,14
- I:
- S: Два одноклассника поступают в институт на разные факультеты. Первый одноклассник поступит с вероятностью 0,5; второй – с вероятностью 0,6. Тогда вероятность того, что оба одноклассника поступят, равна …
- -: 0,7
- +: 0,3
- -: 1,1
- -: 0,03
-
- I:
- S: В первой урне 4 белых и 6 черных шаров. Во второй урне 1 белый и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
- +: 0,25
- -: 0,5
- -: 0,3
- -: 0,15
- I:
- S: В первой урне 2 черных и 8 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
- +: 0,55
- -: 0,11
- -: 0,6
- -: 0,25
- I:
- S: В первой урне 1 черный и 9 белых шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
- +: 0,65
- -: 0,13
- -: 0,7
- -: 0,25
- I:
- S: В первой урне 5 белых и 5 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
- +: 0,6
- -: 0,12
- -: 0,65
- -: 0,1
- I:
- S: В первой урне 2 белых и 8 черных шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
- +: 0,25
- -: 0,05
- -: 0,3
- -: 0,5
- Тестовые задания по теме «Числовые характеристики дискретных случайных величин -10 вопросов»
- I:
- S: Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно… - +: 2
- -: 3
- -: 2,8
- -: 1,5
- I:
- S: Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно… - +: 2,6
- -: 4
- -: 3,4
- -: 2
- I:
- S: Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно… - +: 1,6
- -: 1
- -: 2,6
- -: 0,5
- I:
- S: Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно… - +: 3,2
- -: 5
- -: 4
- -: 2,5
- I:
- S: Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно… - +: 4,4
- -: 4,5
- -: 4,6
- -: 2
- I:
- S: Дан закон распределения вероятностей дискретной случайной величины
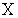 : :

Тогда значение a равно… - +: 0,3
- -: 0,7
- -: -0,7
- -: 0,4
- I:
- S: Дан закон распределения вероятностей дискретной случайной величины
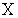 : :

Тогда значение a равно… - +: 0,2
- -: 0,8
- -: -0,8
- -: 0,1
- I:
- S: Дан закон распределения вероятностей дискретной случайной величины
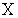 : :

Тогда значение a равно… - +: 0,6
- -: 0,4
- -: -0,4
- -: 0,5
- I:
- S: Дан закон распределения вероятностей дискретной случайной величины
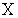 : :

Тогда значение a равно… - +: 0,2
- -: 0,8
- -: -0,8
- -: 0,1
- I:
- S: Дан закон распределения вероятностей дискретной случайной величины
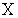 : :

Тогда значение a равно… - +: 0,1
- -: 0,9
- -: -0,9
- -: 0,2
- Тестовые задания по теме «Законы распределения вероятностей непрерывных случайных величин -10 вопросов»
- I:
- S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
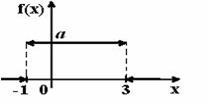
Тогда значение а равно… - +: 0,25
- -: 1
- -: 0,33
- -: 0,2
- I:
- S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
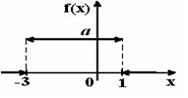
Тогда значение а равно… - +: 0,25
- -: 1
- -: 0,4
- -: 0,2
- I:
- S: График плотности распределения вероятностей непрерывной случайной величины Х имеет вид:
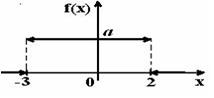
Тогда значение а равно… - +: 0,2
- -: 1
- -: 0,25
- -: 0,4
- I:
- S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид:

Тогда значение a равно… - +:
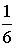 - -: 1
- -:
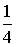 - -:
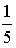 - I:
- S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид:

Тогда значение a равно… - +:
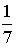 - -: 1
- -:
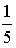 - -:
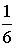 - I:
- S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид:

Тогда значение a равно… - +:
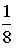 - -: 1
- -:
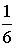 - -:
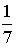 - I:
- S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид:
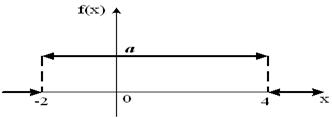
Тогда значение a равно… - +:
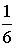 - -: 1
- -:
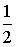 - -:
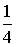 - I:
- S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид:

Тогда значение a равно… - +:
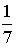 - -: 1
- -:
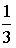 - -:
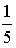 - I:
- S: График плотности распределения вероятностей непрерывной случайной величины X имеет вид:

Тогда значение a равно… - +:
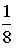 - -: 1
- -:
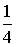 - -:
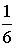 - I:
- S: График плотности вероятностей для нормального распределения изображен на рисунке...
- -:
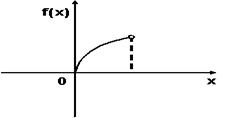 - -:
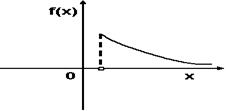 - -:
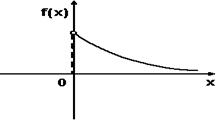 - +:
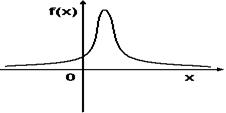 -
-
V1: Теория множеств
V2: Теория
V3: Общая
I: 1 Тема 1-1-1
S: Любая четко определенная совокупность объектов называется
|



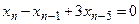 равен …5;
равен …5;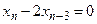 равен …3;
равен …3;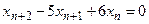 имеет корни +: 2, 3;
имеет корни +: 2, 3;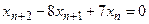 имеет корни 1, 7;
имеет корни 1, 7;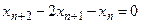 имеет вид
имеет вид 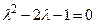
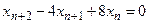 имеет вид
имеет вид 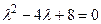
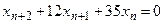 имеет вид
имеет вид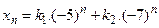
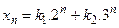
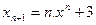 является линейным и неоднородным
является линейным и неоднородным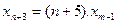 является линейным и однородным
является линейным и однородным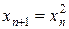 является нелинейным и однородным
является нелинейным и однородным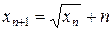 является нелинейным и неоднородным
является нелинейным и неоднородным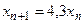 с начальным условием
с начальным условием 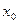 имеет вид
имеет вид 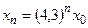
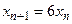 с начальным условием
с начальным условием 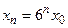
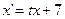 является линейным и неоднородным
является линейным и неоднородным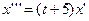 является линейным и однородным
является линейным и однородным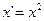 является нелинейным и однородным
является нелинейным и однородным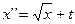 является нелинейным и неоднородным
является нелинейным и неоднородным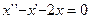 имеет вид
имеет вид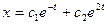
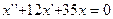 имеет вид
имеет вид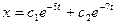
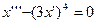 равен 3
равен 3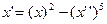 равен 2
равен 2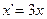 с начальным условием
с начальным условием 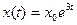
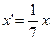 с начальным условием
с начальным условием 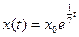
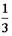
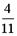
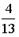
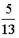





 :
: