Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа арифметико-логического устройств.Содержание книги
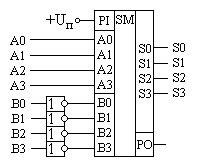
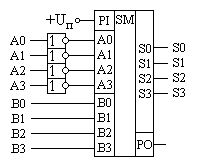
Поиск на нашем сайте
Мы изучили работу двоичных сумматоров, способных осуществить суммирование многоразрядных кодов. Однако кроме операции суммирования часто требуется осуществлять вычитание двоичных кодов. Двоичные коды, при помощи которых можно записывать отрицательные числа рассматривались ранее в курсе информатика Там было показано, что при использовании дополнительных кодов операцию вычитания двух положительных чисел можно заменить операцией суммирования положительного и отрицательного числа, при этом получение отрицательного числа из положительного числа является элементарной операцией. Для этого необходимо проинвертировать число и прибавить к нему 1. Схема вычитателя числа B из числа A приведена на рисунке 52, а схема вычитателя числа A из числа B приведена на рисунке 53.
Рис. 52. Схема вычитателя A − B
Рис. 53. Схема вычитателя B − A
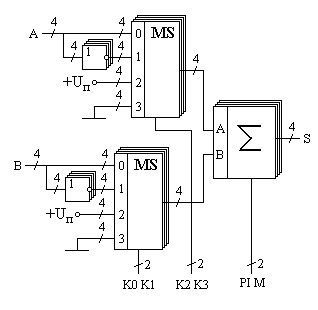
В данных схемах инвертирование числа производится блоком логических инверторов, а прибавление единицы производится подачей питания на вход переноса сумматора PI. Если же потребуется в процессе вычислений изменять арифметическую операцию, то в структурную схему вычислительного устройства можно ввести коммутатор (мультиплексор). Такая схема арифметического устройства приведена на рисунке 54.
Рис. 54. Структурная схема арифметического устройства.
В приведённой на рисунке 50 схеме используются четырёхвходовые мультиплексоры, для управления каждым из которых достаточно двух бит. То есть для управления всей схемы в целом достаточно четырёх проводов управления. Попытаемся построить таблицу операций, которые будет выполнять арифметико-логическое устройство (АЛУ), схема которого приведена на рисунке 3. На результат операции будет влиять вход переноса сумматора PI, поэтому этот вход тоже включим в состав кода, управляющего схемой АЛУ. Операции, которые выполняются арифметической схемой в зависимости от поданного на управляющие линии кода, приведены в таблице (рисунок 55).
Номер строки |
Управляющий код |
Выполняемая операция | |||||||
| K0 | K1 | K2 | K3 | PI | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | S = A + B | ||||
| 1 | 0 | 0 | 0 | 0 | 1 | S = A + B + 1 | ||||
| 2 | 0 | 0 | 0 | 1 | 0 | S = B − A − 1 | ||||
| 3 | 0 | 0 | 0 | 1 | 1 | S = B − A | ||||
| 4 | 0 | 0 | 1 | 0 | 0 | S = B − 1 | ||||
| 5 | 0 | 0 | 1 | 0 | 1 | S = B | ||||
| 6 | 0 | 0 | 1 | 1 | 0 | S = B | ||||
| 7 | 0 | 0 | 1 | 1 | 1 | S = B + 1 | ||||
| 8 | 0 | 1 | 0 | 0 | 0 | S = A − B − 1 | ||||
| 9 | 0 | 1 | 0 | 0 | 1 | S = A − B | ||||
| 10 | 0 | 1 | 0 | 1 | 0 | S = −A − B − 2 | ||||
| 11 | 0 | 1 | 0 | 1 | 1 | S = −A − B − 1 | ||||
| 12 | 0 | 1 | 1 | 0 | 0 | S = −B − 2 | ||||
| 13 | 0 | 1 | 1 | 0 | 1 | S = −B − 1 | ||||
| 14 | 0 | 1 | 1 | 1 | 0 | S = −B − 1 | ||||
| 15 | 0 | 1 | 1 | 1 | 1 | S = −B | ||||
| 16 | 1 | 0 | 0 | 0 | 0 | S = A − 1 | ||||
| 17 | 1 | 0 | 0 | 0 | 1 | S = A | ||||
| 18 | 1 | 0 | 0 | 1 | 0 | S = −A − 2 | ||||
| 19 | 1 | 0 | 0 | 1 | 1 | S = −A − 1 | ||||
| 20 | 1 | 0 | 1 | 0 | 0 | S = −2 | ||||
| 21 | 1 | 0 | 1 | 0 | 1 | S = −1 | ||||
| 22 | 1 | 0 | 1 | 1 | 0 | S = −1 | ||||
| 23 | 1 | 0 | 1 | 1 | 1 | S = 0 | ||||
| 24 | 1 | 1 | 0 | 0 | 0 | S = A | ||||
| 25 | 1 | 1 | 0 | 0 | 1 | S = A + 1 | ||||
| 26 | 1 | 1 | 0 | 1 | 0 | S = −A − 1 | ||||
| 27 | 1 | 1 | 0 | 1 | 1 | S = −A | ||||
| 28 | 1 | 1 | 1 | 0 | 0 | S = −1 | ||||
| 29 | 1 | 1 | 1 | 0 | 1 | S = 0 | ||||
| 30 | 1 | 1 | 1 | 1 | 0 | S = 0 | ||||
| 31 | 1 | 1 | 1 | 1 | 1 | S = +1 | ||||
Рис. 55. Коды математических операций арифметического устройства
Проанализируем эту таблицу. Если на все управляющие входы подать низкий потенциал (Управляющий код равен 0000), то к входу сумматора будут подключены коды A и B без инверсии. В этом случае будет производиться операция суммирования. Эта ситуация отображена первыми двумя строками таблицы выполняемых операций. Операция вычитания осуществляется второй, третьей, восьмой и девятой строкой. В этом случае один из операндов поступает на вход сумматора через блок инверторов. Правда для получения дополнительного кода не хватает единицы, но её можно подать на вход переноса сумматора PI. Ещё одной часто используемой операцией является увеличение числа на единицу или уменьшение числа на единицу. Эти операции позволяют легко организовывать циклы в программе и переходить от предыдущего операнда к следующему. Такие операции могут быть выполнены при помощи кодов, записанных в строках четыре, семь, шестнадцать и двадцать пять. Кроме того, схема арифметического устройства может просто передавать на выход любой из входных кодов без изменения, что позволяет осуществлять копирование данных (суммирование с константой ноль) через это устройство без дополнительных схем коммутации.
При небольшом изменении схемы такое устройство может быть преобразовано в схему, которая позволяет осуществлять не только арифметические, но и логические операции. Для этого нужно вести дополнительный коммутатор, который будет разрывать цепи переноса между разрядами. Эта управляющая цепь обычно называется M. Подобная схема реализована в микросхеме АЛУ К155ИП3 (иностранный аналог 74181). Ее внутренняя схема приведена на рисунке 56.
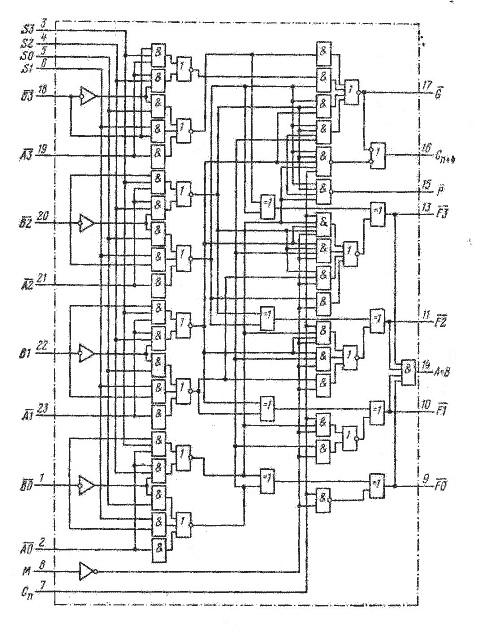
Рис. 56. Схема арифметико-логического устройства (АЛУ) К155ИП3
Подчеркнём основную особенность полученного устройства. Арифметико-логические устройства позволяют выбирать вид выполняемой операции при помощи кода, подаваемого на специальные выводы микросхемы. Это позволяет программировать одно и то же устройство для выполнения различных функций. Разработка такого устройства позволило обменивать большую скорость выполнения отдельных операций на сложность реализуемого алгоритма, что, в конце концов, привело к разработке микропроцессорных систем. Развитие этих систем изменило окружающий нас мир.
|
| Поделиться: |
