Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что изучает начертательная геометрия?Содержание книги
Поиск на нашем сайте
Начертательная геометрия Ответы на теоретические вопросы к экзамену Оглавление 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 Что изучает начертательная геометрия? Начертательная геометрия изучает методы изображения пространственных форм на плоскости и способы решения геометрических задач по этим изображениям.
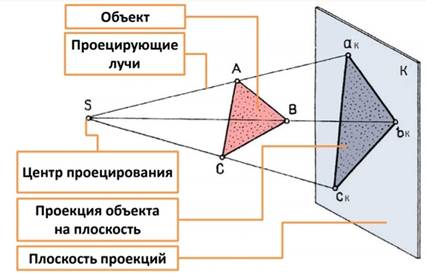
В чем заключается отличие центрального проецирования от параллельного? Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S – центра проецирования. Используется при построении перспективных изображений.
Параллельным проецированием называют такое проецирование, при котором все проецирующие прямые параллельны заданному направлению S. Используется для построения ортогональных и аксонометрических проекций.
В чем сущность метода проекций? Метод проецирования является основным методом начертательной геометрии. Проекция предмета на плоскости является его изображением на плоскости с помощью проецирующих лучей. А так как любой предмет можно представить совокупностью множества точек, то проецирование – это построение проекций отдельных точек. Сущность проецирования заключается в том, чтобы через заданные точки мысленно проводились проецирующие лучи до пересечения их с какой-либо плоскостью. Точки пересечения проецирующих лучей на этой плоскости и называются проекциями заданных точек. В зависимости от способа проведения проецирующих лучей различают центральное и параллельное проецирование.
Взаимное расположение прямых. Параллельные прямые Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Пересекающиеся прямые Это прямые, лежащие в одной плоскости и имеющие одну общую точку, которую называют точкой пересечения прямых.
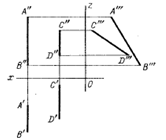
Скрещивающиеся прямые Прямые, которые не лежат в одной плоскости На рис. 86 изображены две скрещивающиеся прямые общего положения: хотя одноименные проекции и пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, параллельной линиям связи L"L' и М"М', т. е. эти прямые не пересекаются между собой.
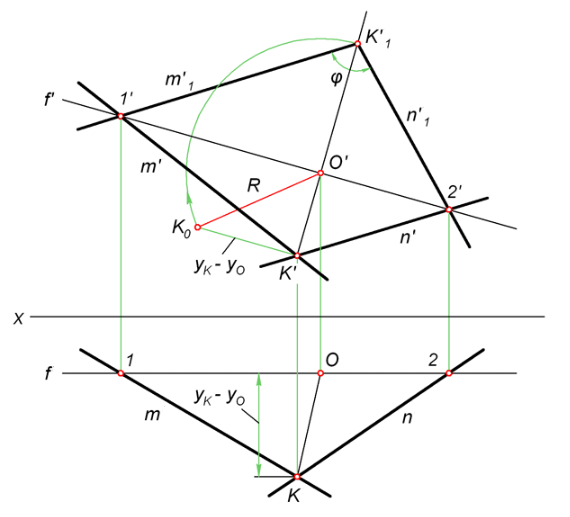
7. Перечислите способы определения натуральной величины угла между двумя пересекающимися прямыми. У пересекающихся прямых точки пересечения одноименных проекций прямых находятся на одной линии связи. Для того, чтобы угол между прямыми проецировался в натуральную величину необходимо, чтобы обе стороны этого угла были параллельны данной плоскости проекций, т.е. чтобы плоскость угла была плоскостью уровня. При решении этой задачи наиболее рациональным, а поэтому, наиболее распространенным путем решения, является преобразование чертежа способом вращения плоскости вокруг одной из ее прямых уровня. При этом способе плоскость общего положения сразу преобразуется в плоскость уровня.
Приведенный ниже пример иллюстрирует нахождение угла между пересекающимися прямыми m и n способом вращения вокруг фронтали.
Последовательность построений: 1) В произвольном месте чертежа проводим фронталь f. Она пересекает прямые m и n в точках 1 и 2. Определяем их недостающие проекции.
2) Через точку K' проводим перпендикуляр к f'. На пересечении этого перпендикуляра с фронталью находится проекция центра вращения O'. По линии связи определяем положение т. O. 3) Находим величину радиуса R поворота точки K. Для этого перпендикулярно O'K' откладываем отрезок K'K0 = yk – yo. Таким образом, R равен O'K0 – гипотенузе прямоугольного треугольника O'K'K0. 4) Проводим дугу радиусом R до её пересечения с перпендикуляром O'K' в точке K'1. Соединяем K'1 c точками 1' и 2'. Натуральная величина угла между прямыми m и n равна углу ϕ при вершине K'1. Cледы плоскости. Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости. Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой(как для построения любой прямой). На рисунке 5.8 показано нахождение следов плоскости ∑ (АВС). Фронтальный след плоскости ∑ 2, построен, как прямая соединяющая две точки 1 2 и 2 2, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости ∑. Горизонтальный след ∑1 – прямая, проходящая через горизонтальный след прямой АВ и ∑x.
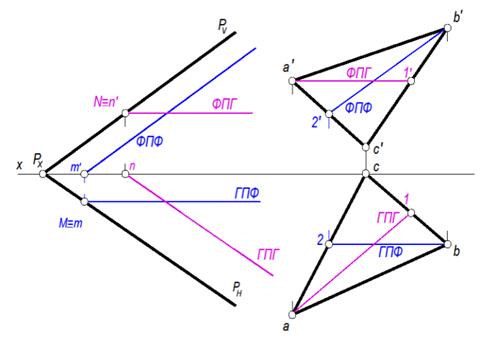
Построение горизонтали Проводим фронтальную проекцию горизонтали (ФПГ) параллельно оси ОХ, затем строим горизонтальную проекцию горизонтали (ГПГ) параллельно PH. Построение фронтали Проводим горизонтальную проекцию фронтали (ГПФ) параллельно оси OХ, затем сроим фронтальную проекцию фронтали (ФПФ) параллельно PV (на рисунке показано синим)
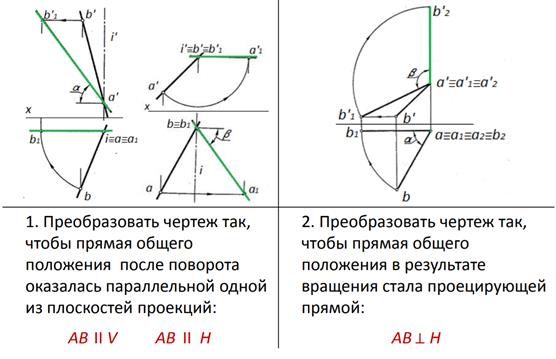
Способ вращения Сущность метода: в результате вращения вокруг некоторой оси прямая или плоскость должны занять частное положение относительно неизменной системы плоскостей проекций. Основные задачи (доп. инфа, на всякий случай, в тетради по проекционке и в методичке этого нет, но в презентации есть): Способ совмещения Вращение плоскости вокруг оси, совпадающей с плоскостью проекций, т.е. вокруг следа плоскости, является частным случаем вращения вокруг линии уровня плоскости. Способ совмещения заключается в том, что заданную плоскость Р вместе с расположенными в ней геометрическими элементами вращают вокруг одного из ее следов РН или РV до совмещения с соответствующей плоскостью проекций Н или V. Все геометрические элементы (прямые и другие линии, фигуры), лежащие в заданной плоскости, изображаются в натуральную величину на плоскости проекций, с которой производится совмещение. Совмещение позволяет найти величину плоской фигуры по ее проекциям или построить проекции плоской фигуры, лежащей в какой-либо плоскости, по заданным ее размерам. Если плоскость задана следами, то задача совмещения ее с плоскостью проекций сводится к построению совмещенного положения одного из следов, так как другой след, принимаемый за ось вращения, не меняет своего положения.
Плоскость Р совмещаем с плоскостью Н вращением вокруг следа РН. Используя горизонталь плоскости, на которых лежат вершины треугольника, находим совмещенные положения В0, С0 этих вершин и получаем треугольник А0В0С0, равный заданному.
Теорема Монжа
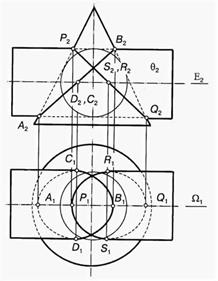
Если две поверхности второго порядка описаны около третьей того же порядка, то они пересекаются по двум плоским кривым.
Начертательная геометрия Ответы на теоретические вопросы к экзамену Оглавление 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 Что изучает начертательная геометрия? Начертательная геометрия изучает методы изображения пространственных форм на плоскости и способы решения геометрических задач по этим изображениям.
|
||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.136 (0.011 с.) |

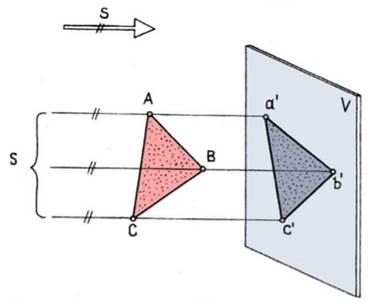
 Параллельные прямые НЕ параллельные прямые.
Параллельные прямые НЕ параллельные прямые. 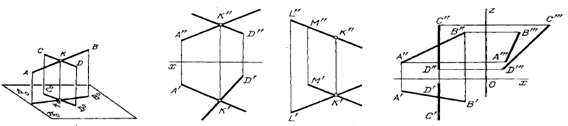 Если прямые линии пересекаются, то их одноименные проекции пересекаются между собой в точке, которая является проекцией точки пересечения этих прямых.
Если прямые линии пересекаются, то их одноименные проекции пересекаются между собой в точке, которая является проекцией точки пересечения этих прямых.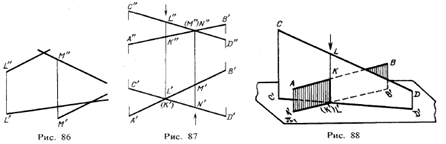
 п
п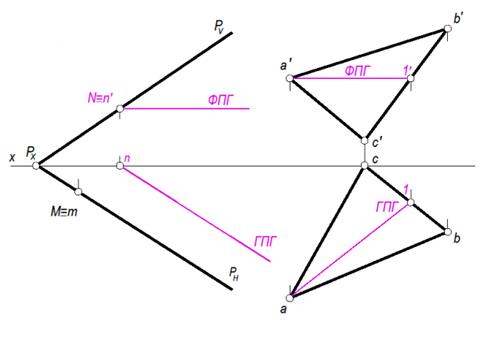
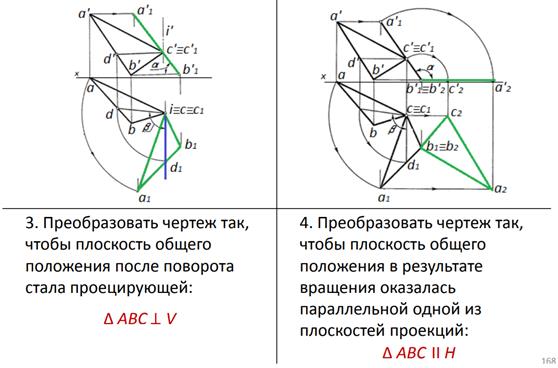
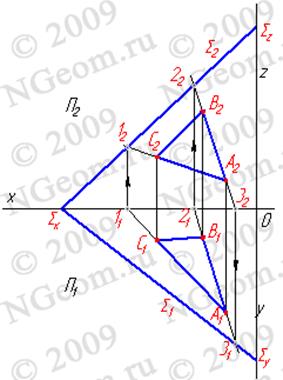
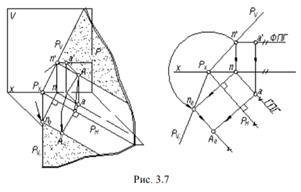 Как видно из рис. 3.7, для определения совмещенного следа Pv0 при вращении плоскости Р вокруг следа РH достаточно найти совмещенное положение N0 любой точки N следа РV. На рис. 3.7 показано также совмещение точки А (а, а'), лежащей в плоскости Р, с плоскостью Н при использовании горизонтали.
Как видно из рис. 3.7, для определения совмещенного следа Pv0 при вращении плоскости Р вокруг следа РH достаточно найти совмещенное положение N0 любой точки N следа РV. На рис. 3.7 показано также совмещение точки А (а, а'), лежащей в плоскости Р, с плоскостью Н при использовании горизонтали. Задача. Найти натуральную величину треугольника ABC, расположенного в плоскости Р общего положения (рис. 3.8).
Задача. Найти натуральную величину треугольника ABC, расположенного в плоскости Р общего положения (рис. 3.8).