
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Организация работы с массивамиСодержание книги
Поиск на нашем сайте
В подавляющем большинстве практических задач, связанных с обработ- кой числовой информации, приходится иметь дело с конечными числовыми по- следовательностями, образование членов в которых не всегда подчиняется ка- кой-либо зависимости и не может быть связано с заранее связанной формулой. В таких случаях для обозначения членов последовательности используется та- кая структура данных, как массив. В терминах алгоритмизации и программиро- вания говорят, что для обозначения массивов используются индексированные переменные. Массив – одномерная или многомерная совокупность фиксированного числа однотипных элементов. Массив характеризуется идентификатором (име- нем), числом измерений (количеством индексов), и длиной каждого измерения. Например, в одномерном массиве длина массива равна количеству его элемен- тов; в двумерном массиве (матрице), состоящей из N строк и M столбцов коли- чество элементов – N·M. Каждый элемент массива обозначается именем и ин- дексом (индексами). Значение индекса указывает на местоположение элемента в массиве. Одномерные массивы могут обозначаться в постановке задачи, например, следующим образом: {ai}, i = 1,n; или {a1, a2, … an}. При написании алгоритмов для обозначения элемента массива записывают а(i), т. е. при выполнении алго- ритма обращение к элементу массива осуществляется по имени массива и ин- дексу, указанному в скобках рядом с именем С точки зрения памяти компьютера одномерный массив – это последова- тельность ячеек, расположенных в одну линию. Пример массива приведен ниже. 1 2 3 4 5 6 7 8
Массив имеет имя q, длину 8. Для того чтобы можно было отличить одну ячейку массива от другой ячейки этого же массива, их нумеруют. Нумерация ячеек обычно начинается с 1. Номер ячейки массива называется его индексом, а константа в ячейке – элементом массива. Первый элемент массива q имеет зна- чение 2,3; последний имеет значение –4,7; элемент с номером 6 имеет значение 0. Теперь становится возможной работа с отдельной ячейкой такого массива. Например, команда q(7):= 8.2 означает, что в 7-ю ячейку массива q надлежит записать константу 8.2. Команда r(41):= q(2) + q(5) означает, что нужно сло- жить константы, записанные во 2 и 5-ю ячейки массива q, и результат записать в 41-ю ячейку одномерного массива r. Эту же операцию можно описать други- ми словами: 41-му элементу массива r присвоить значение суммы 2 и 5-го эле- ментов массива q. Для алгоритмов обработки (преобразования) массивов используются цик- лы с известным числом повторений. Счетчик цикла совпадает с индексом эле- мента массива. Цикл обеспечивает перебор элементов массива по соответст- вующему индексу измерению и повторяется столько раз, какова длина массива в этом измерении. Ввод (вывод) элементов массива осуществляется при использовании ал- горитмов циклической структуры с заданным числом повторений, в которых количество вложенных друг в друга циклов определяется размерностью масси- ва, а количество изменений переменных каждого из циклов - максимально воз- можным количеством элементов массива в рассматриваемом измерении.
- нахождение суммы элементов массива; - нахождение минимального и/или максимального элемента; - поиск в массиве элемента, равного заданному значению; - формирование из заданного массива нового по заданному условию; - упорядочение элементов массива. 4.2. Преобразование одномерных массивов Задача 20.
Если число очков на каждом шаре рассматривать как элемент массива, то задача сводится к определению суммы положительных и количества отрица- тельных элементов массива, состоящего из 57 элементов, например, D1, D2,..., D57. Алгоритмы вычисления суммы и подсчета количества нам уже известны. Исходные данные: {Di} i = 1…57. Выходные данные: SUM – сумма положительных элементов; KOL – количество отрицательных элементов. Рабочие переменные: i – счетчик цикла, совпадает с номером элемента массива; SUM – текущее значение суммы; KOL – счетчик отрицательных элементов. Алгоритмы подсчета суммы элементов последовательности и количества элементов, удовлетворяющих заданному условию, мы уже изучали. При работе с одномерными массивами используются циклы с известным числом повторений, в том числе и ввод-вывод массива. Цикл обеспечивает последовательный перебор элементов массива. Каждый элемент массива обозначается как D(i), где D – имя массива, i – его номер. Значение переменной i определяется из блока модификации: при первом выполнении цикла i равно 1, т. е. берется первый элемент массива, при втором выполнении цикла i равно 2, т. е. берется второй элемент массива, и т. д. При i, равном 57, цикл выполняется последний раз, соответственно берется последний элемент массива. Алгоритм приведен в блок-схеме 29 и программе МАСС1. Рассмотрим массив D:
При выполнении алгоритма переменные KOL и SUM получают началь- ное значение 0. При переборе элементов массива с помощью цикла, каждый элемент сравниваем с нулем. Если значение элемента больше нуля, то увеличи- ваем значение суммы, если элемент меньше нуля, то увеличиваем значение ко- личества. Так, при i = 1 значение SUM = 0 + 2,3 = 2,3; при i = 2 значение KOL = 0 + 1 = 1; при i = 3 никаких вычислений не проводим; при i = 4 значение SUM = 2,3 + 4,4 = 6,7; при i = 5 значение KOL = 1 + 1 = 2; при i = 6 значение SUM = 6,7 + 8 = 14,7 и т. д.
ВЕЩЕСТВЕННЫЙ D(57), SUM ЦЕЛЫЙ i, KOL ЦИКЛ по i от 1 до 57 шаг 1
ВВОД D(i)
КОНЕЦ ЦИКЛА
KOL:= 0 SUM:= 0
ЦИКЛ по i от 1 до 57 шаг 1
ЕСЛИ D(i) > 0 ТО SUM:= SUM + D(i) КОНЕЦ ЕСЛИ
ЕСЛИ D(i) < 0 ТО KOL:= KOL + 1 КОНЕЦ ЕСЛИ КОНЕЦ ЦИКЛА ВЫВОД SUM, KOL
КОНЕЦ
Блок-схема 29
Программа МАСС1
Задача 21.
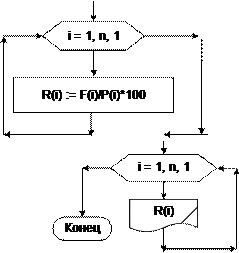
Для решения задачи прежде необходимо подобрать структуры данных, в которых будет храниться исходная и выходная информация. Поскольку имеет- ся n цехов, то паны – это последовательность чисел. Аналогично, данные о фак- тическом выпуске продукции – это другая последовательность чисел. И по- скольку процент выполнения плана нужно рассчитать для каждого цеха, то это еще одна последовательность чисел. Каждую из последовательностей представим в виде одномерного массива. Пусть это будут соответственно массивы P, F и R. Разберем задачу на конкретном примере. Пусть на предприятии 10 цехов, выпуск продукции измеряется в тыс. р.: n = 10; P = {95, 58, 100, 55, 82, 75, 60, 96, 88, 62}; F = {90, 58, 80, 60, 85, 72, 90, 95, 86, 70}; в результате выполнения алгоритма должен быть получен следующий массив: R = {95, 100, 80, 109, 104, 96, 150, 99, 98, 113}. Формализованная постановка задачи выглядит следующим образом. Исходные данные: n – количество элементов массива = количеству цехов; {Pi} i = 1…n – одномерный массив «план», т. е. Pi – план, выставленный i- му цеху, где i – номер цеха; {Fi} i = 1…n – одномерный массив «факт», т. е. Fi – выпуск продукции i-м цехом, где i – номер цеха. Выходные данные: {Ri} i = 1…n – одномерный массив «процент», т. е. Ri – процент выполнения плана i-м цехом, где i – номер цеха. Рабочие переменные: i – счетчик цикла, совпадает с номером элемента массива, соответственно с номером цеха; Алгоритм приведен в блок-схеме 30. Комментарии к алгоритму. Сначала вводим значение n. Далее идет цикл для ввода элементов первого исходного массива, затем – цикл для ввода эле- ментов второго исходного массива. После вода исходных данных организуем цикл для перебора элементов исходных массивов. В теле цикла формируется очередной (i-й) элемент нового массива R, который рассчитывается по формуле вычисления процента. После завершения цикла все n элементов нового массива будут вычислены. Для вывода значений элементов нового массива опять орга- низуем цикл.
Блок-схема 30 Рассмотрим теперь часто встречающуюся задачу поиска минимального и максимального значения в массиве чисел. Очевидно, что для нахождения мак- симума или минимума, нужно перебрать все элементы массива и сравнить их между собой. Но сравнивать каждый элемент с каждым не имеет смысла. Про- ще поступить следующим образом: последовательно сравнивать два значения, выбрать из них большее – для поиска максимума или меньшее – для поиска минимума; следующий элемент массива сравнивать с этим большим (меньшим) значением, выбрать большее (меньшее) из них, и переходить к следующему элементу и т. д., пока не дойдем до конца массива. Для осуществления такого алгоритма необходима рабочая переменная для хранения текущего значения максимума (минимума). Часто нужно найти не просто максимальное (минимальное) значение в массиве, но и сам максимальный (минимальный) элемент, т. е. номер элемента, принимающего максимальное (минимальное) значение. В этом случае необхо- дима еще одна рабочая переменная для хранения значения текущего номера. Задача 22.
Переформулируем постановку задачи в терминах структур данных.
Теперь задан массив R, состоящий из 10 элементов: n = 10; R = {95, 100, 80, 109, 104, 96, 150, 99, 98, 113}. Максимальный элемент – седьмой элемент массива со значением 150, минимальный элемент – третий со значением 80. Исходные данные: N – количество элементов в массиве; {Ri} i = 1…n – заданный массив. Выходные данные: MAX – максимальный элемент в массиве; nommax – номер максимального элемента; MIN – минимальный элемент в массиве; nommim – номер минимального элемента. Рабочие переменные: i – счетчик цикла, совпадает с номером элемента массива; MAX– текущее значение максимума; nommax – текущее значение номера максимального элемента; MIN – текущее значение минимума; nommim – текущее значение номера минимального элемента.
Алгоритм нахождения максимального элемента массива заключается в следующем. Сначала предполагается, что максимальный элемент в массиве – это первый элемент, его значение запоминается в переменной, для хранения максимума. Затем просматриваются все остальные элементы массива (с помо- щью цикла, повторяющегося n раз), сравниваются с текущим значением макси- мума, если очередной элемент оказывается больше текущего значения макси- мума, то текущее значение максимума меняется на значение этого элемента. Соответственно, запоминается номер «последнего» наибольшего элемента. Алгоритм нахождения минимального элемента аналогичен. На блок-схеме 31 изображен алгоритм решения этой задачи, а программа MaxMin реализует этот алгоритм.
MIN ЦЕЛЫЙ N, i, nommax, nommin ВВОД N
ЦИКЛ по i от 1 до N шаг 1 ВВОД A(i) КОНЕЦ ЦИКЛА
MAX:= A(1) nommax:=1 MIN:= A(1) nommin:=1
ЦИКЛ по i от 1 до N шаг 1
ЕСЛИ A(i) > MAX ТО MAX:= A(i) nommax:= i КОНЕЦ ЕСЛИ ЕСЛИ A(i) < MIN ТО MIN:= A(i) nommin:= i КОНЕЦ ЕСЛИ
КОНЕЦ ЦИКЛА ВЫВОД MIN, nommin, MAX, nommax КОНЕЦ ЦИКЛА КОНЕЦ
Блок-схема 31 Программа MaxMin
Задача 23.
Переформулируем постановку задачи в терминах структур данных.
Разберем задачу на примере. Пусть имеется 12 магазинов. Данные об объемах продаж за месяц хранятся в массиве Х: n = 12; Х = {95, 58, 100, 100, 40, 75, 40, 96, 100, 62, 78, 90}; максимальное значение – 100, минимальное значение – 40, среднее между ми- нимумом и максимумом – 70. В результате работы алгоритма элементы массива Х должны принять следующие значения: Х = {95, 58, 70, 70, 70, 75, 70, 96, 70, 62, 78, 90}. Исходные данные: N – количество элементов в массиве; {Xi} – заданный массив. Выходные данные: {Xj} – результат замены. Рабочие переменные: I – счетчик цикла, совпадает с номером элемента массива; MAX – максимальное значение в массиве; MIN – минимальное значение в массиве; S – среднее значение между минимумом и максимумом. Условие задачи подразумевает, что в массиве имеются одинаковые эле- менты. В связи с этим в нем может оказаться несколько элементов, равных мак- симальному значению и несколько элементов, равных минимальному значению элементов массива. Требуется все такие элементы заменить средним арифмети- ческим между значениями минимума и максимума. Решение задачи разбивается на два этапа. Во-первых, требуется найти значение максимума и минимума. Во-вторых, заменить значения элементов, удовлетворяющих заданному условию на новое значение. Алгоритм решения этой задачи состоит из двух последовательно выпол- няемых друг за другом циклов. Первый обеспечивает перебор всех элементов исходного массива и нахождения максимума и минимума. Эти алгоритмы мы уже рассматривали в предыдущей задаче. После завершения цикла рассчитыва- ется их среднее арифметическое значение: сумма минимума и максимума, де- ленная на два. Второй цикл осуществляет повторный просмотр элементов ис- ходного массива. В теле цикла происходит сравнение элементов со значениями минимума и максимума. Если текущий элемент равен хотя бы одному из них, выполняется замена значения этого элемента на значение среднего арифмети- ческого.
На блок-схеме 32 изображен алгоритм решения этой задачи.
Рассмотрим пример задачи. Требуется сформировать новый массив зара- нее неизвестной длины из элементов, удовлетворяющих некоторому условию: из заданного массива в новый нужно выбрать элементы, удовлетворяющие ка- кому-либо условию. Мы не знаем заранее, сколько элементов окажется в новом массиве, поэтому нужна переменная – счетчик элементов в новом массиве. Сначала она принимает значение ноль. По мере того как будут встречаться элементы, удовлетворяющие заданному условию, счетчик элементов увеличи- вается на единицу. Задача 24.
Переформулируем постановку задачи в терминах структур данных.
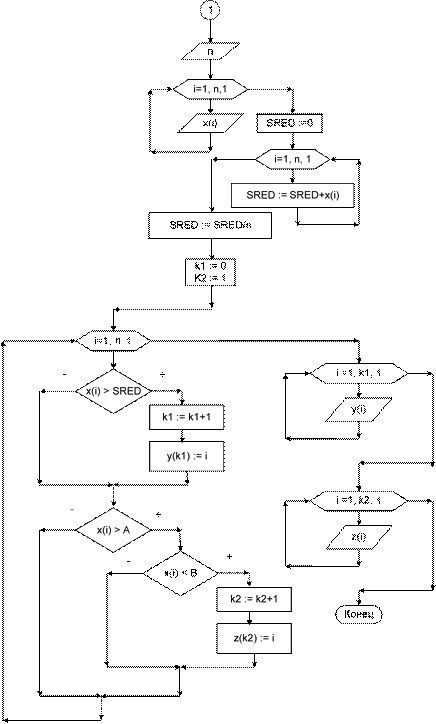
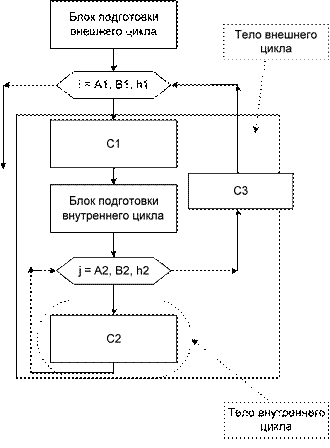
{zj} элементы, попадающие в интервал от A до B. Исходные данные: n – количество элементов в массиве; {xi} – заданный массив; A, B –заданные числа. Выходные данные: {yj} – результат выбора элементов; {zj} – результат выбора элементов. Рабочие переменные: i – счетчик цикла, совпадает с номером элемента массива; SRED – сумма и среднее значение; k1 – счетчик элементов в новом массиве {yj}; k2 – счетчик элементов в новом массиве {zj}. На блок-схеме 33 изображен алгоритм решения этой задачи. Комментарии к алгоритму. После ввода и проверки исходных данных алгоритм решения этой задачи состоит из двух последовательно выполняемых друг за другом циклов. Первый обеспечивает перебор всех элементов исходно- го массива и вычисление суммы. После завершения цикла рассчитывается среднее значение. Перед началом второго цикла подготавливаются счетчики элементов новых массивов, сначала они равны нулю. Второй цикл осуществля- ет повторный просмотр элементов исходного массива. В теле цикла происходит сравнение элементов со средним значением и с заданными числами А и В. Если текущий элемент оказался больше вычисленного среднего, то увеличивается на единицу счетчик элементов результатного массива и в него заносится новый элемент с номером, соответствующим этому счетчику. В качестве значения элемента нового массива берется номер элемента исходного массива, удовле- творяющего проверяемому условию. В результате количество элементов нового массива будет равно значению счетчика. Аналогичные действия выполняются в том случае, если текущий элемент массива оказался больше А, но меньше В, т. е. номер элемента помещается во второй результатный массив.
Блок-схема 33
Сложные циклы Возможны случаи, когда внутри тела цикла необходимо повторять неко- торую последовательность действий, т. е. организовать внутренний цикл. Такая структура получила название «цикл в цикле» или вложенные циклы. Глубина вложения циклов (т. е. количество вложенных друг в друга циклов) может быть различной. Цикл называется сложным, если он содержит два или более вложенных один в другой циклов. Сложные (вложенные циклы) используются в задачах поиска и перебора одномерных массивов, для сортировки массивов, при работе с многомерными массивами и в других случаях для перебора множества дан- ных по разным измерениям. Простейший случай сложного цикла – цикл в цикле. Цикл, тело которого содержит другой цикл, называется внешним, а вложенный в него цикл – внут- ренним. Структурно детерминированный цикл в цикле выглядит следующим об- разом:
Рис. 18. Сложный цикл
Если A1 = 1,B1 = n, h1 = 1 и A2 = 1, B2 = m, h2 = 1, то тело внутреннего цикла выполняется m раз, а тело внешнего цикла n раз. Таким образом, блоки С1, С3 и блок подготовки внутреннего выполняются nраз, а блок С2 (n * m) раз. При реализации цикла в цикле следует придерживаться следующих правил: - тело внутреннего цикла должно содержаться полностью в теле внешне- го цикла; - назначение рабочих переменных и счетчиков внешнего и внутреннего циклов должно быть строго разграничено. Задача 25.
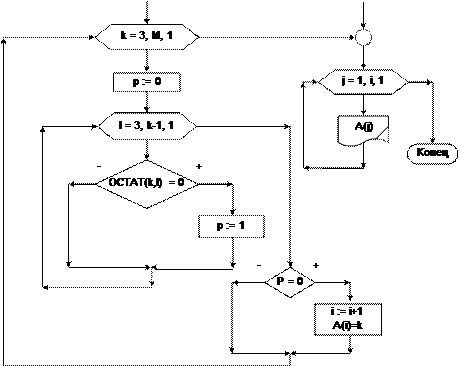
Число называется простым, если оно имеет только два делителя: единицу и само себя. Простые числа, не превосходящие 20, это: 2, 3, 5, 7, 11, 13, 17, 19. Алгоритм решения этой задачи состоит в следующем. Нужно взять оче- редное целое число в интервале от 2 до М. Пусть это будет число k, и прове- рить, делится ли оно без остатка, хотя бы на одно из предшествующих чисел (кроме 1). То есть для каждого k нужно перебрать все числа от 2 до k-1. Если хотя бы одно число из интервала от 2 до k-1 оказалось делителем числа k, то число k – непростое. Таким образом, для составления алгоритма необходимо использовать «цикл в цикле». В общем случае понадобится: - внешний цикл, например, со счетчиком k – для перебора чисел в интер- вале от 2 до М; - внутренний цикл – для перебора чисел от 2 до k-1. Счетчик внешнего цикла k и есть проверяемое число. Если оно оказалось простым, его нужно запомнить в качестве очередного элемента формируемого массива простых чисел. Для сокращения времени выполнения алгоритма мож- но отбросить из рассмотрения четные числа, предварительно записав в качестве первого элемента формируемого массива число 2. Тогда внешний цикл будет организован по k от 3 до M c шагом 2, т. е. будут перебираться и проверяться только нечетные числа. А внутренний цикл будет организован от 3 до k-1 с ша- гом 1, поскольку проверку делимости на 2 уже не нужно осуществлять. Для за- поминания результатов проверки делимости нам понадобиться вспомогатель- ная переменная – признак делимости. Такого рода переменная называется «флаг», она принимает значение 1, если событие наступило, и 0, если событие не наступило. Алгоритм решения задачи приведен на блок-схеме 34. Исходные данные: M – заданное число (M>1). Выходные данные: {Aj} – массив простых чисел. Рабочие переменные: k – счетчик внешнего цикла, проверяемое число; L – счетчик внутреннего цикла, проверяемый де- литель; i – счетчик элементов в формируемом массиве; p – признак равен 1, если k разделилось нацело хотя бы на одно из значений L, и равен 0, если k ни разу не разделилось ни на одно из значений L.
Блок-схема 34
Комментарии к алгоритму. Если заданное число равно двум, то выход- ной массив будет состоять из единственного элемента, равного 2. Если задан- ное число больше двух, то сначала в первый элемент массива заносим число 2, и задаем начальное значение счетчику элементов в массиве, равное 1. Вешний цикл по k обеспечивает перебор всех натуральных нечетных чисел, не превос- ходящих заданного M. В теле внешнего цикла для каждого нового проверяемого числа обнуляем признак делимости p и организуем внутренний цикл для перебора натуральных чисел, меньших k. В теле внутреннего цикла проверяем, делится ли число k на число, совпадающее со счетчиком внутреннего цикла без остатка. Если хотя бы один раз деление без остатка произошло, то признак p получает значение 1, и это означает, что число k не простое, в противном случае (ни одно L не оказа- лось делителем k) значение признака останется без изменения. Закончив внутренний цикл, но находясь в теле внешнего цикла, проверя- ется значение признака p. Если признак p остался равным 0, то число k – про- стое, заносим его в качестве очередного элемента массива A, увеличив при этом счетчик элементов этого массива. Задача 26.
состоящего из различных чисел. Подобный алгоритм часто приходится составлять при проверке правиль- ности ввода элементов массива, если в условии задачи сказано, что массив со- стоит из различных чисел. Для этого при вводе очередного элемента массива необходимо проверять отсутствие такого значения среди уже введенных эле- ментов. Если такое значение уже есть, то нужно ввести этот же элемент масси- ва, но с другим значением, если вводимого значения не существует, то перехо- дим на ввод следующего элемента массива. Алгоритм представлен на блок- схеме 35. Исходные данные: N – количество элементов в массиве; {Xi} – заданный массив. Выходные данные: {Xj} – введенный массив. Рабочие переменные: i – счетчик цикла, совпадает с номером вводимого элемента массива; j – счетчик цикла, совпадает с номером введенного ранее элемента массива; p – признак: равен 1, если в массиве уже есть эле- мент с таким значением, и равен 0, если в массиве нет элемента с вводимым значением.
Блок-схема 35
Комментарии к алгоритму. Первый элемент массива X(1) вводится отдель- но. Затем организуется цикл для ввода остальных элементов: со 2-го по N-й. Для этого элемента обнуляется признак совпадений. Организуется цикл для перебо- ра уже существующих в массиве элементов. Если значение вводимого элемента совпало хотя бы с одним значением ранее введенных элементов, то признак совпадений в результате выполнения внутреннего цикла получит значение 1. После завершения внутреннего цикла проверяется значение признака. Если оно осталось равным 0, то осуществляется переход на продолжение внешнего цикла при следующем значении i, т. е. на ввод следующего элемента массива; в про- тивном случае осуществляется возврат на ввод нового значения этого же эле- мента массива.
Алгоритмы сортировки Сортировка (упорядочение) массива данных – это перестановка его эле- ментов в порядке возрастания или убывания значений. Сортировка массивов – одна из центральных проблем обработки данных. Это связано, прежде всего, с тем, что на практике часто встречаются задачи поиска в различных реестрах, справочниках, словарях и т. д. Как правило, объемы таких массивов очень большие, поэтому для облегчения поиска и выполнения других процедур обра- ботки данных массивы сортируются. Примеры упорядоченных реестров: спи- сок группы студентов – упорядочен по алфавиту; таблица выигрышных номе- ров лотерейных билетов и т. п. Сортировать элементы можно по неубыванию (a1 <= a2 <=...<= an) и по невозрастанию (a1 >= a2 >=…>= an). Задачу упорядочения элементов массива можно решить разными спосо- бами. Разными исследователями было разработано множество методов сорти- ровки. Основные из них можно разбить на три группы: - сортировки выбором; - сортировки обменом; - сортировки включением Рассмотрим в общих чертах суть этих методов для случая упорядочения по возрастанию. Сортировки выбором Алгоритм метода заключается в следующем: по- следовательно просматривают элементы a(1), a(2),...,a(n), находят такое i, что а(i) является минимальным значением в массиве. Меняют местами а(i) с а(1). Затем выполняют то же самое, не рассматривая тот элемент, который уже по- ставили на место и т. д. Сортировки обменом Алгоритм метода таков: последовательным про- смотром элементов a(1), a(2),...,a(n), находят наименьшее i такое, что a(i) > a(i+1). Затем меняют a(i) и a(i+1) местами и возобновляют просмотр с a(i+1) элемента и т. д. Тем самым наибольшее число передвинется на последнее место. Следую- щие просмотры опять начинают с начала последовательности, уменьшая количе- ство просматриваемых элементов на 1. Массив будет упорядочен после про- смотра, в котором участвовали только первый и второй элементы. Сортировки включением Алгоритм метода состоит в следующем: после- довательно просматривают элементы a(1), a(2),...,a(n) и каждый новый элемент a(i) вставляют на подходящее место в уже упорядоченную совокупность a(i-1). Это место определяется последовательным сравнением a(i) с упорядоченными элементами a(1), …, a(i-1). Представьте, что перед вами лежит колода карт. Для сортировки карт об- меном вы должны разложить карты на столе лицевой стороной вверх и затем менять местами те карты, которые расположены в неправильном порядке, делая это до тех пор, пока колода карт не станет упорядоченной. Для сортировки выбором вы должны разложить карты на столе, выбрать самую младшую карту и взять ее в руку. Затем вы должны из оставшихся на столе карт вновь выбрать наименьшую по значению карту и поместить ее поза- ди той карты, которая уже имеется у вас в руке. Этот процесс вы должны про- должать до тех пор, пока все карты не окажутся у вас в руках. Поскольку каж- дый раз вы выбираете наименьшую по значению карту из оставшихся на столе, то после завершения такого процесса, карты у вас в руке будут отсортированы. Для сортировки вставкой вы должны держать карты в своей руке, пооче- редно снимая карту с колоды. Каждая взятая вами карта помещается в новую колоду на столе, причем она ставится на соответствующее место. Колода будет отсортирована, когда у вас в руке не окажется ни одной карты. Каждый из этих методов может быть реализован с помощью разных, несколько отличных друг от друга, алгоритмов. Например, сортировка по возрастанию выбором может заключаться в поиске максимального элемента и перестановки его на последнее место. Сортировка по убыванию выбором выполняется либо поиском миниму- ма и перестановки его на последнее место, либо поиском максимума и переста- новки его на первое место. Каждый из методов имеет свои преимущества и недостатки, но они име- ют сходства: - все алгоритмы сортировки реализуются с помощью сложного цикла, обеспечивающего многократный перебор элементов массива; - все алгоритмы имеют обязательные действия: сравнение и перестанов- ка двух элементов массива. Задача 27.
элементов в порядке убывания методом выбора наименьшего элемента. Опишем подробнее этот алгоритм. Сначала в исходном массиве опреде- ляется минимальный элемент и его номер. Найденный элемент меняется места- ми с последним. Таким образом, получается, что наименьший элемент попадает на свое место – в конец массива. Затем из рассмотрения исключается послед- ний элемент и ищется минимальный среди оставшихся элементов. Найденный минимум меняется с предпоследним элементом массива. Таким образом, полу- чается, что второй наименьший элемент попадает на свое место – на второе ме- сто с конца массива. Далее из рассмотрения исключается и этот элемент, и про- цесс продолжается до тех пор, пока не останется один элемент массива, кото- рый окажется на первом месте. Это будет максимальный элемент. В общем случае процесс упорядочения закончится через (n-1) повторений поиска мини- мального значения и его перестановки на свое место. Рассмотрим сказанное на примере пошагового выполнения этого алгоритма. Пусть задан массив a: {4 15 2 31 16 28}, n=6
Таким образом, для реализации алгоритма необходимо организовать цикл в цикле. Внешний цикл обеспечивает многократный просмотр элементов мас- сива. Тело внешнего цикла содержит алгоритм поиска минимального значения, который тоже является циклическим процессом, и перестановку найденного минимального элемента с последним элементом из рассматриваемой совокуп- ности. Исходные данные: N – количество элементов в массиве; {ai} – заданный массив. Выходные данные: {ai} – упорядоченный массив. Рабочие переменные: i – счетчик внешнего цикла, совпадает с номером просмотра; j – счетчик внутреннего цикла, совпадает с номе- ром элемента массива; min – значение минимального элемента; nom – номер минимального элемента; k – номер «последнего» элемента при очередном просмотре.
Алгоритм представлен на блок-схеме 36.
Задача 28.
n элементов в порядке убывания методом обмена. Алгоритм упорядочения по убыванию методом обмена заключается в следующем. В массиве заданной длины последовательно сравниваются между собой два соседних элемента. Если предыдущий элемент меньше последующе- го, то они переставляются местами. Таким образом, минимальный элемент ста- новится на последнее место. Одновременно ведется счетчик перестановок. По- сле того, как весь массив просмотрен, проверяется счетчик перестановок. Если он равен нулю, это значит, что массив уже упорядочен. В этом случае, про- смотр заканчивается, полученный массив выводится и программа завершается. Если же счетчик перестановок неравен нулю, то просмотр массива начинается сначала и осуществляться перестановка элементов, при этом длина массива уменьшается на единицу, так как последний элемент уже можно не сравнивать. Очевидно, если длина массива – N, то в худшем случае, массив надо бу- дет просмотреть (N – 1) раз. Если же некоторые элементы исходного массива стоят в порядке убывания, то просмотр массива можно закончить раньше, ис- пользуя счетчик перестановок. Таким образом, алгоритм упорядочения реали- зуется с помощью цикла в цикле, где внешний цикл обеспечивает многократ- ный просмотр массива, а внутренний цикл служит для просмотра всех элемен- тов массива. При этом значение счетчика внешнего цикла равно количеству просмотров и, соответственно, числу элементов, уже стоящих на месте в конце массива, которые в дальнейшем не рассматриваются, а счетчик внутреннего цикла при первом просмотре изменяется от 1 до N – 1, при втором – от 1 до N – 2, при третьем – от 1 до N – 3 и т. д. Описанный метод называется еще методом пузырька, так как минимальный элемент как бы всплывает (постепенного пере- двигается) на последнее место. Исходные данные: N – количество элементов в массиве; {Ai}, – заданный массив. Выходные данные: {Ai}, – упорядоченный массив. Рабочие переменные: J – счетчик внешнего цикла; sp – счетчик перестановок; i – счетчик внутреннего цикла; r – рабочая переменная для перестано
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Для ввода – вывода элементов одномерного массива открывается цикл с количеством повторений, равным количеству членов массива, а затем в цикле осуществляется поэлементный ввод (вывод) значений каждого из членов мас- сива {Ai} (рис. 16 и 17). При этом переменная цикла i отслеживает местораспо- ложение вводимого или выводимого элемента в массиве.
Для ввода – вывода элементов одномерного массива открывается цикл с количеством повторений, равным количеству членов массива, а затем в цикле осуществляется поэлементный ввод (вывод) значений каждого из членов мас- сива {Ai} (рис. 16 и 17). При этом переменная цикла i отслеживает местораспо- ложение вводимого или выводимого элемента в массиве.
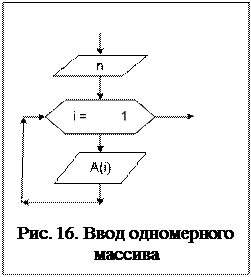 Наиболее частые задачи преобразования массивов это:
Наиболее частые задачи преобразования массивов это: В урне находится 57 шаров, на каждом из которых записано положи- тельное или отрицательное число очков. Определить сумму положи- тельных очков, записанных на шарах, и количество шаров с отрицатель- ными очками.
В урне находится 57 шаров, на каждом из которых записано положи- тельное или отрицательное число очков. Определить сумму положи- тельных очков, записанных на шарах, и количество шаров с отрицатель- ными очками.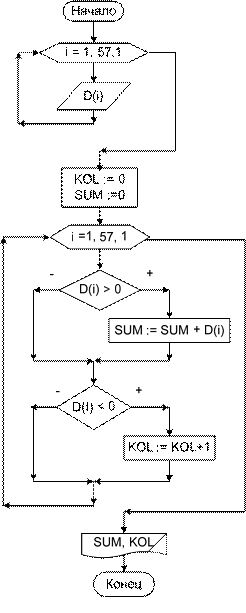 НАЧАЛО
НАЧАЛО
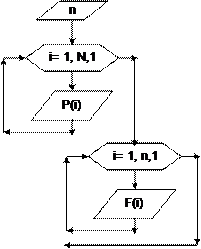
 Пусть теперь требуется определить номер цеха с максимальным (в про- центном выражении) выпуском продукции и с минимальным выпуском продукции.
Пусть теперь требуется определить номер цеха с максимальным (в про- центном выражении) выпуском продукции и с минимальным выпуском продукции. В заданном одномерном массиве различных чисел определить мини- мальный и максимальный элементы и их номера.
В заданном одномерном массиве различных чисел определить мини- мальный и максимальный элементы и их номера.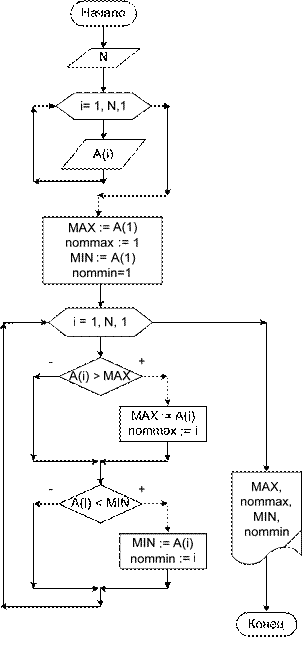
 НАЧАЛО ВЕЩЕСТВЕННЫЙ D(57) ВЕЩЕСТВЕННЫЙ MAX,
НАЧАЛО ВЕЩЕСТВЕННЫЙ D(57) ВЕЩЕСТВЕННЫЙ MAX, Предприятие занимается розничной торговлей и имеет в своей структуре N магазинов. В начале каждого месяца магазинам выставляются планы продаж в тыс. р. Исходными данными для выставления планов являются отчеты каждого магазина об объемах продаж. Поскольку минимальные и максимальные продажи могут быть обусловлены независящими от са-
Предприятие занимается розничной торговлей и имеет в своей структуре N магазинов. В начале каждого месяца магазинам выставляются планы продаж в тыс. р. Исходными данными для выставления планов являются отчеты каждого магазина об объемах продаж. Поскольку минимальные и максимальные продажи могут быть обусловлены независящими от са- мого магазина факторами, для таких магазинов в качестве плана выстав- ляется среднее значение между максимальными и минимальными про- дажами. Для остальных магазинов в качестве плана выставляются объе- мы продаж за предыдущий месяц.
мого магазина факторами, для таких магазинов в качестве плана выстав- ляется среднее значение между максимальными и минимальными про- дажами. Для остальных магазинов в качестве плана выставляются объе- мы продаж за предыдущий месяц. В заданном одномерном массиве, состоящем из N, все элементы, равные либо максимальному, либо минимальному значению элементов массива, заменить средним значением между минимумом и максимумом.
В заданном одномерном массиве, состоящем из N, все элементы, равные либо максимальному, либо минимальному значению элементов массива, заменить средним значением между минимумом и максимумом.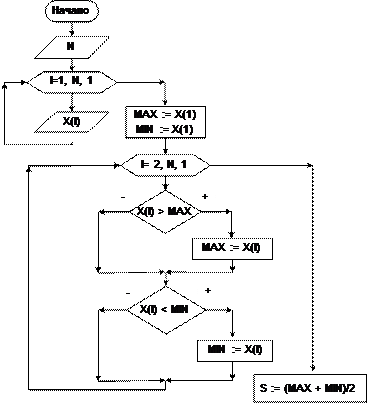
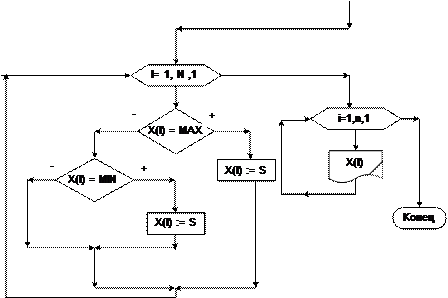 Блок-схема 32
Блок-схема 32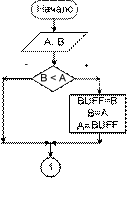
 Сформировать массив простых чисел, не превосходящих заданного чис- ла М.
Сформировать массив простых чисел, не превосходящих заданного чис- ла М.




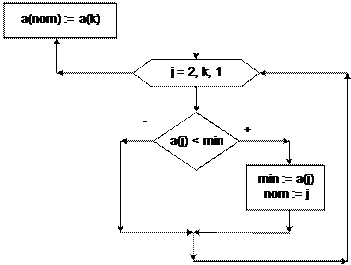 Блок-схема 36
Блок-схема 36


