Реализация циклических процессов

Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них перемен- ных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами, т. е. цикл – это повторяющаяся совокупность действий Алгоритмы, содержащие циклы, называется циклическими.

Алгоритм циклической структуры предусматривает многократное повто- рение действий в одной и той же последовательности, но при разных значениях некоторой специально изменяемой величины. Циклические алгоритмы позво- ляют существенно сократить объем программы за счет многократного выпол- нения группы повторяющихся вычислений, так называемого тела цикла.

Рассмотрим пример циклического алгоритма для задачи нахождения наи- большего общего делителя (НОД) для двух заданных натуральных чисел. Этот алгоритм был предложен древнегреческим математиком Евклидом

Для начала приведем словесную запись алгоритма.

1) Обозначить первое число буквой M, второе – буквой N.

2) Сравнить M и N.

3) Если M > N, то из M вычесть N, принять новое значение M и перейти к п. 2 алгоритма, иначе перейти к п. 4.

4) Если M < N, то из N вычесть M, принять новое значение N и перейти к п. 2 алгоритма, иначе перейти к п. 5.

5) Принять НОД = M.

Комментарии к алгоритму. Алгоритм заключается в том, что многократ- но сравниваются два числа и из большего вычитается меньшее. Большее число принимает новое значение полученной разности. Как только два сравниваемых числа станут равны, их значение и есть наибольший общий делитель. Таким образом, в описанном алгоритме к п. 5 приходим в том случае, если M не больше N и M не меньше N (значит M равно N). Значение любой из этих пере- менных, например M, будет являться НОД.

Подставив конкретные числовые значения, например 40 и 28, можно про- верить его «работу»:

Полагаем M = 40 и N = 28.

Сравниваем M и N.

Так как 40 > 28, то присваиваем M = 40 – 28 = 12.

Сравниваем M и N.

Так как 12 < 28, то присваиваем N = 28 – 12 = 16.

Сравниваем M и N.

Так как 12 < 16, то присваиваем N = 16 – 12 = 4.

Сравниваем M и N.

Так как 12 > 4, то присваиваем M = 12 – 4 = 8.

Сравниваем M и N.

Так как 8 > 4, то присваиваем M = 8 – 4 = 4

Сравниваем M и N.

Так как 4 не > 4 и 4 не < 4, то присваиваем НОД = 4

 

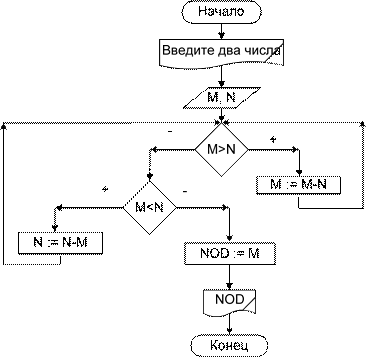
Заметим, что описание алгоритма содержит всего пять пунктов, а его вы- полнение требует большего числа шагов (в нашем примере 13). Это обусловле- но тем, что некоторые действия (п. 2, 3, 4), как и было предписано алгоритмом, повторялись несколько раз.

Составим блок-схему описанного алгоритма:

 

Блок-схема 8

 

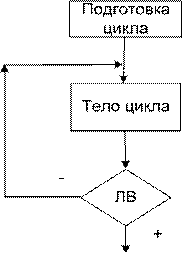
Блок-схема 8 не удовлетворяет правилам структурного построения алго- ритмов. Описанный алгоритм можно перестроить таким образом, чтобы на- званные правила соблюдались.

Для записи алгоритмов циклической структуры в соответствии со струк- турным подходом построения блок-схем существуют две управляющие струк- туры, каждая из которых состоит из трех блоков:

- подготовка цикла;

- тело цикла;

- условный блок.

Блок подготовки цикла обеспечивает задание начальных значений пере- менных, используемых и модифицируемых в теле цикла. Повторяющиеся дей- ствия образуют тело цикла. Проверка условия обеспечивает выход из цикла.

В управляющей структуре «Цикл-до» (рис. 12) логический блок задает условие выхода из цикла: если логическое выражение принимает значение

«ИСТИНА», то цикл завершается, в противном случае управление передается на повторение тела цикла. Такой цикл называется еще «цикл с постусловием», поскольку проверка на завершение цикла осуществляется после выполнения тела цикла. Эта управляющая структура обеспечивает выполнение тела цикла хотя бы один раз. Цикл повторяется до выполнения заданного условия.

В управляющей структуре «Цикл-пока» (рис. 13) логический блок задает условие продолжения цикла: если логическое выражение принимает значение

«ИСТИНА», то управление передается на выполнение тела цикла, в противном случае цикл завершается. Такой цикл называется еще «цикл с предусловием», поскольку проверка на завершение цикла осуществляется до выполнения тела цикла. Цикл повторяется пока выполнения заданное условие. Следуя такой структуре, тело цикла может не выполниться ни разу.

 

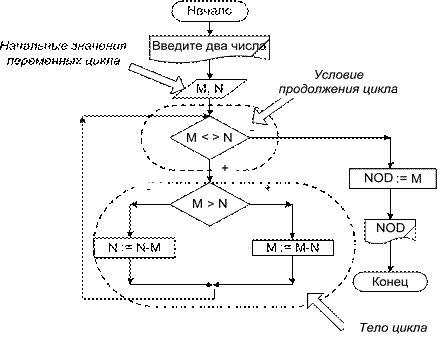
В теле цикла могут использоваться любые блоки, кроме блоков «Начало» и «Конец». В нем обязательно должна присутствовать, так называемая пере- менная цикла, значение которой вычисляется по одной и той же схеме каждый раз при выполнении тела цикла, т. е. при очередном повторении цикла эта пе- ременная получает новое значение. Эта же переменная используется в условии продолжения цикла или выхода их него. Следовательно, при организации цик- лов необходимо предусмотреть задание начального значения переменной цик- ла, и условие, при выполнении которого произойдет завершение цикла.

Различают детерминированные циклы (циклы с известным числом повто- рений), итерационные (с неизвестным числом повторений) и сложные (вложен- ные) циклы. Циклы, в теле которых нет других встроенных в них циклов, назы- вают простыми. В противном случае их относят к сложным.

Представим в виде блок-схемы алгоритм Евклида нахождения наиболь- шего общего делителя (НОД) для двух заданных натуральных чисел несколько изменив его таким образом, чтобы соблюсти правила структурного составления блок-схем. Для этого воспользуемся УС «Цикл с предусловием» (блок-схема 9).

 

 

Блок-схема 9

 

В составленной блок-схеме в УС «Цикл с предусловием» отсутствует как таковой блок подготовки. Его роль играет блок ввода значений исходных дан- ных. Кроме этого, в отличие от большинства алгоритмов циклического типа здесь присутствуют две переменных цикла. Их начальное значение задается в блоке ввода, в теле цикла обе они меняют свое значение. В условии продолже- ния цикла эти две переменные сравниваются между собой.

 

Совестная запись алгоритма:

1) Обозначить первое число буквой M, второе – буквой N.

2) Пока M <> N выполнять п. 3 – п. 5, иначе перейти на п. 6.

3) Сравнить M и N.

4) Если M > N, то из M вычесть N, принять новое значение M, иначе из

N вычесть M, принять новое значение N.

5) Перейти на п. 2.

6) Принять НОД = M.

 

Рассмотрим две задачи о депозитных вкладах, которые помогут понять, когда используются циклы с пост- и предусловием.

Задача 8.

Вычислить сумму вклада, которую получит вкладчик депозитного вкла- да под N % годовых через G лет, если его первоначальный вклад состав- лял X р. Проценты начисляются и капитализируются ежеквартально. Капитализация процентов – это их начисление и причисление к сумме вклада, на которую вновь начисляются проценты. Условие депозитного вклада: вкладчик не забирает никакие суммы денег до окончания срока вклада.

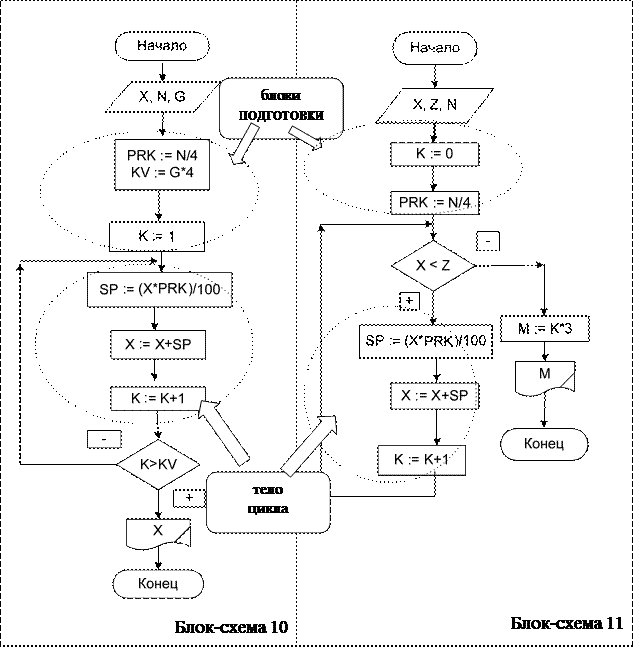
Исходные данные: X – первоначальная сумма вклада (р.), N – годовой процент, G – срок вклада (лет).

Выходные данные: X – конечная сумма вклада.

Рабочие переменные: PRK – ежеквартальный процент, KV – количество кварталов в течение срока вклада, SP – сумма процентов для начисления, K – счетчик кварталов (переменная цикла), X – текущая сумма вклада.

Формулы, рассчитывающие результаты:

PRK = N / 4; KV = G · 4; SP = X · PRK / 100.

Алгоритм решения задачи описан в блок-схеме 10.

Задача 9.

Определить, какое время (в мес.) должен пролежать депозитный вклад под N % годовых для достижения суммы Z р., если первоначальный вклад составляет X р. Условия депозитного вклада: вкладчик не забира- ет никакие суммы денег до окончания срока вклада; проценты начисля- ются и капитализируются ежеквартально.

Исходные данные: X – первоначальная сумма вклада (руб.), N – годовой процент, Z – нужная сумма, накопленная на вкладе.

Выходные данные: M – количество месяцев (требуемый срок вклада).

Рабочие переменные: PRK – ежеквартальный процент, SP – сумма про- центов для начисления, K – счетчик кварталов, X – текущая сумма вклада (пе- ременная цикла).

Формулы, рассчитывающие результаты:

PRK = N / 4; SP = X · PRK / 100; M = K · 3

Алгоритм решения задачи описан в блок-схеме 11.

 

Не вдаваясь в подробности вычислений, рассмотрим структуру циклов в том и другом алгоритме. В первом алгоритме используется цикл с постуслови- ем. В качестве переменной цикла, проверяемой в условии выхода из цикла, вы- ступает счетчик цикла (K), совпадающий с порядковым номером квартала, для которого известно в каком диапазоне он должен изменяться (от 1 до KV). Тело цикла будет повторяться столько раз, сколько значений получит переменная K. Цикл выполняется до того момента, как только значение K превысит значение

KV. Результат работы алгоритма – значение переменной X – накопленная сум- ма вклада. Значение переменной X каждый раз при выполнении тела цикла увеличивается на значение переменной SP, аналогично тому, как пополняется сумма вклада на сумму начисленных процентов.

Во втором алгоритме используется цикл с предусловием. В качестве пе- ременной цикла, проверяемой в условии продолжения цикла, выступает вычис- ляемая переменная X – накопленная сумма вклада. Цикл будет выполняться, пока значение X меньше значения Z – требуемой суммы вклада. В алгоритме присутствует переменная K, в которой считается количество повторений тела цикла. Значение переменной K используется для расчета получения результата работы алгоритма, т. е. количества кварталов. В этом алгоритме, если значение переменной X сразу окажется больше или равно Z, тело цикла не выполнится ни разу, тогда результатом работы алгоритма будет число 0, т. е. вклад нис- колько не должен лежать, чтобы получить указанную сумму.

Таким образом, видим, что в теле цикла обоих алгоритмов выполняются одинаковые действия:

- вычисляется начисленная сумма процентов;

- вычисляется новая сумма вклада;

- вычисляется порядковый номер квартала.

С другой стороны, для решения поставленных задач в алгоритмах циклы должны быть организованы разными способами. Это касается и блоков подго- товки и структуры цикла.

 

Для более детального рассмотрения вычислительного процесса к этим блок-схемам вернемся позже, когда рассмотрим некоторые стандартные приемы вычислений.