Линейные и нелинейные структуры данных

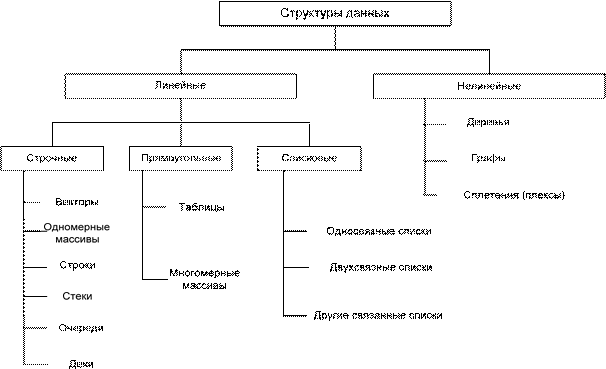
Важный признак структуры данных – характер упорядоченности ее эле- ментов. По этому признаку структуры можно делить на линейные и нелиней- ные (рис. 2).

 

 

Рис. 2. Классификация структур данных по характеру упорядоченности элементов

 

В зависимости от характера взаимного расположения элементов в памяти вычислительной машины линейные структуры можно разделить на структуры с последовательным расположением элементов, которые в свою очередь подраз- деляются на строчные и картезианские (прямоугольные) и структуры с произ- вольным связанным распределением элементов в памяти. Строчные структуры данных – это векторы, одномерные массивы, строки, стеки, очереди, деки. Прямоугольные структуры данных это: таблицы и многомерные массивы. К списковым структурам относятся различные линейные связанные списки. При- мерами нелинейных структур являются графы, деревья, разветвленные связан- ные списки (многосвязанные списки, сплетения).

Линейные структуры данных – это структуры, в которых связи между элементами не зависят от выполнения какого-либо условия. Понятия одномер-

ных и многомерных массивов рассмотрим в следующих главах, посвященных изучению алгоритмам работы с этими структурами данных. Здесь более под- робно остановимся на рассмотрении строчных структур данных: стеки, очере- ди, деки. Эти структуры отличаются друг от друга способами включения и ис- ключения элементов.

Стек – это последовательность элементов, в которой включение и ис- ключение элемента осуществляется с одной стороны последовательности. Вы- борка элементов осуществляется в порядке, обратном их засылке (LIFO – Last Input – First Output, последним пришел – первым вышел). Это статическое или динамическое множество. Добавление элементов в стек и выборка из него вы- полняются из одного конца, называемого вершиной стека. Другие операции со стеком не определены. При выборке элемент исключается из стека. Условно стек можно представить в виде стакана с шариками (рис. 3).

 

Рис. 3. Схема стека

 

Стеки широко применяются в системном программном обеспечении, компиляторах, в различных рекурсивных алгоритмах. Известные примеры сте- ка в жизнедеятельности людей – стопка тарелок, которые составляются друг на друга, а затем, что бы их помыть тарелки берутся сверху; железнодорожный разъезд для сортировки вагонов, когда в тупик загоняются вагон под номерами, например, 1, 2, 3, а выводятся оттуда в обратном порядке: 3, 2, 1; пистолетный патронный магазин; и др.

В экономических информационных системах стеки используются для моде- лирования некоторых производственных процессов. Для объяснения идеи стека воспользуемся аналогией. Многие люди складывают приходящие письма стопкой на журнальном столике. Когда появится свободная минута, они обрабатывают на- копившуюся почту сверху вниз. Сначала они открывают письмо, находящееся на вершине стопки, и выполняют необходимое действие – оплачивают счет, выбра- сывают письмо и т. д. Разобравшись с первым письмом, они переходят к следую- щему конверту, который теперь оказывается на верху стопки, и разбираются с ним. В конечном итоге, они добираются до нижнего письма (которое теперь ока- зывается верхним). Принцип «начать с верхнего письма» отлично работает, при условии, что вся почта может быть обработана за разумное время.

Стековую архитектуру также можно сравнить с процессом выполнения различных дел во время рабочего дня. Вы трудитесь над долгосрочным проек-

том (A), но ваш коллега просит временно прерваться и помочь ему с другим проектом (B). В ходе работы над B к вам заходит бухгалтер, чтобы обсудить ваш отчет по командировочным расходам (C). Во время обсуждения вам срочно звонят из отдела продаж, и вы тратите несколько минут на диагностику своего продукта (D). Разобравшись со звонком D, вы продолжаете обсуждение C; по- сле завершения C возобновляется проект B, а после завершения B вы возвра- щаетесь к проекту A. Проекты с более низкими приоритетами «складываются в стопку», ожидая, пока вы к ним вернетесь.

Очередь – это динамически изменяемый упорядоченный набор элементов. Добавление элементов в очередь производится с одного конца (хвост очереди), а выборка – с другого (голова) в соответствии с правилом FIFO (First In – First Out). Условно очередь можно представить в виде трубки с шариками (рис. 4).

 

Добавление элемента

К

О н е ц

Н

а ч а л о

Удаление элемента

 

Рис. 4. Схема очереди

 

Очереди очень часто встречаются в реальной жизни, например, около банков или ресторанов быстрого обслуживания. В решении экономических за- дач очереди используются в моделировании систем массового обслуживания, и в таких частных задачах, например как расчет себестоимости проданных това- ров по методу FIFO.

Дек – линейная структура (последовательность элементов) в которой операции включения и исключения элементов могут выполняться как с одного, так и с другого конца последовательности.

Очереди, стеки и деки имеют две характерные особенности: структуры дан- ных имеют строгие правила доступа к хранящимся в них данным, причем в ре- зультате выполнения операций извлечения данные, в сущности, уничтожаются. Другими словами, доступ к элементу в стеке или очереди приводит к его удале- нию, и если этот элемент не сохранить где-либо в другом месте, он теряется. Кро- ме того, и в стеке, и в очереди используется один последовательный участок па- мяти. В отличие от стека или очереди, связанный список допускает гибкие спосо- бы доступа, поскольку каждый фрагмент информации имеет ссылку на следую- щий элемент данных в цепочке. Кроме того, операция извлечения не приводит к удалению из списка и уничтожению элемента данных. В принципе, для этой цели необходимо ввести дополнительную специальную операцию удаления.

В списковых структурах логический порядок данных определяется указа- телями. Любая списковая структура представляет собой набор элементов, каждый

из которых состоит минимум из двух полей: в одном из них размещается элемент данных или указатель на него, а в другом – указатель на следующий элемент спи- ска (рис. 5). Связанные списки могут быть односвязными и двусвязными. Одно- связный список содержит ссылку на следующий элемент данных. Двусвязный список содержит ссылки как на последующий, так и на предыдущий элементы списка. Выбор типа применяемого списка зависит от конкретной задачи.

 

Рис. 5. Схема односвязного списка

 

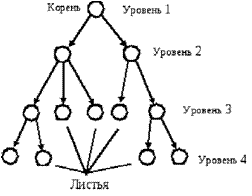
Нелинейные структуры данных – это структуры данных, у которых связи между элементами зависят от выполнения определенного условия. Примеры нелинейных структур – деревья, графы, многосвязанные списки. Древовидные структуры – это иерархические структуры, состоящие из набора вершин и ре- бер, каждая вершина содержит определенную информацию и ссылку на верши- ну нижнего уровня.

Дерево – иерархическая структура данных, хранящая набор элементов. Каждый элемент имеет значение и может указывать на ноль или более других элементов (потомков). На каждый элемент указывает только один другой эле- мент. Единственным исключением является корень дерева, на который не ука- зывает ни один элемент. Входящие в дерево элементы называются его верши- нами (узлами). Вершины, не имеющие потомков, называются листьями (рис. 6). Степень дерева – максимальная степень всех вершин. Степень вершины – чис- ло ее непосредственных потомков. Высота (глубина) дерева – максимальный уровень его листьев. Высота пустого дерева равна – 1.

 

Рис. 6. Дерево

 

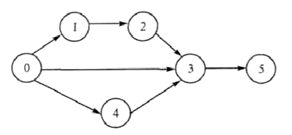
Дерево характеризуется следующими свойствами:

- существует единственный элемент (узел или вершина), на который не ссылается никакой другой элемент, и который называется корнем;

- начиная с корня и следуя по определенной цепочке указателей, содержа- щихся в элементах, можно осуществить доступ к любому элементу структуры;

- на каждый элемент, кроме корня, имеется единственная ссылка, т. е. каждый элемент адресуется единственным указателем

Наиболее распространенной структурой данных является бинарное (дво- ичное) дерево – древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым сыном. Очевидно, что дерево, как структура данных является рекурсивной, т. е. каждый узел в дереве, если он не является листом, задает поддерево, корнем которого он является. Для практиче- ских целей обычно используют подвид бинарного дерева – двоичное дерево поиска. Двоичное дерево поиска – это двоичное дерево, для которого выполня- ются следующие дополнительные условия (свойства дерева поиска):

Оба поддерева – левое и правое, являются двоичными деревьями поиска:

- у всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X;

- у всех узлов правого поддерева того же узла X значения ключей дан- ных не меньше, нежели значение ключа данных узла X.

Для целей реализации двоичное дерево поиска можно определить так. Двоичное дерево состоит из узлов (вершин) – записей вида (data, left,

right), где data – некоторые данные привязанные к узлу, left и right – ссылки на узлы, являющиеся детьми данного узла – левый и правый сыновья соответст- венно. Для оптимизации алгоритмов конкретные реализации предполагают также определения поля parent в каждом узле (кроме корневого) – ссылки на родительский элемент (прошитое дерево поиска).

Данные (data) обладают ключом (key), на котором определена операция сравнения «меньше». В конкретных реализациях это может быть пара (key, value) – (ключ и значение), или ссылка на такую пару, или простое определение операции сравнения на необходимой структуре данных или ссылке на нее.

Для любого узла X выполняются свойства дерева поиска: key[left[X]] < key[X] ≤ key[right[X]], т. е. ключи данных родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого.

Над деревьями определены следующие основные операции:

- поиск узла с заданным ключом;

- добавление нового узла;

- удаление узла (поддерева).

Граф – это сложная нелинейная многосвязная динамическая структура, отображающая свойства и связи сложного объекта. Объекты представляются как вершины, или узлы графа, а связи – как дуги, или ребра (рис. 7). Для разных об- ластей применения виды графов могут различаться направленностью, ограниче- ниями на количество связей и дополнительными данными о вершинах или ребрах.

 

Рис. 7. Граф

 

В экономике графы используются, например, для планирования работ. В основе процесса планирования лежит некоторый сценарий, представляющий собой граф, состоящий из вершин – пошагового описания действий и дуг – от- ношений между ними. Такой граф дает возможность, сравнивая альтернативы, планировать действия для достижения поставленной цели.

Графы и деревья получили широкое практическое применение потому, что они являются естественным и удобным способом изображения и дальней- шего анализа различных сложных систем. С их помощью решают задачи управления экономическими объектами (дерево целей, организационная струк- тура предприятия, дерево переборов вариантов). Графы используют также для иллюстрации классификаций в различных областях знаний при построении ие- рархических структур сложных систем.